Multiplicação e divisão de frações
Produzido por Marcelo LuizTeoria
Fala aí! Hoje vamos aprender sobre multiplicação e divisão de frações. Falar de frações é sempre um pouquinho assustador, né? Mas eu te garanto que com tempo e prática, você vai dominar tudo o que vamos ver aqui.
Dado o tanto que é comum trabalharmos com frações em assuntos mais avançados de matemática, é extremamente importante dominar estas técnicas aqui, pra já chegar lá na frente dando voadora em qualquer continha que parecer mais complicada envolvendo frações, beleza?
Se você preferir, pode ver esse esse conteúdo na forma desse vídeo maravilhoso 👇
Não deixa de conferir também:
Multiplicação de Frações
Entre todas as operações de frações, essa aqui é a mais fácil, pois resolvemos do jeito mais direto possível. Olha só, para resolvermos a seguinte multiplicação de frações
basta multiplicarmos o numerador da primeira fração com o numerador da segunda fração e o denominador da primeira com o denominador da segunda. Ou seja, “o de cima vezes o de cima e o de baixo vezes o de baixo”. Então:
E se tivermos mais de duas frações? Sem segredo, continuamos multiplicando o que tá em cima com o que tá em cima e o que tá embaixo com o que tá embaixo.
Tá, mas e quando temos uma fração multiplicando um número inteiro? Tipo assim:
Continuamos multiplicando o que tá em cima com o que tá em cima e o que tá embaixo com o que tá embaixo. Mas ué, não tem nada embaixo do 5?!

É só você lembrar que um número dividido por 1 dá sempre o próprio número! Então podemos reescrever aquela continha da seguinte forma:
Aí é só resolvermos como já aprendemos.
Simplificações
Em alguns casos, vamos nos deparar com algo do tipo:
E aí temos algumas opções. Podemos resolver exatamente da mesma forma que o anterior:
Mas não é muito legal deixar isso aí no nosso resultado final, porque 30 dividido por 3 dá um número inteiro! Então, é sempre bom simplificarmos a fração e colocar o resultado, quando ele for um inteiro.
(No exemplo anterior, deixamos na forma 10/3 pois 10 dividido por 3 dá 3,333... aí é preferível deixar na forma de fração mesmo, vai depender do que o seu professor pedir, beleza?)
Agora, algumas vezes pode ser mais difícil lembrar se um número é múltiplo ou divisor de outro. Por exemplo, na conta
pode não ser claro logo de cara que a fração 84/3 dá um número inteiro. Mas olha só que interessante, se eu reescrever a conta original da seguinte forma:
Fica mais fácil de perceber que aquele 12 pode ser dividido pelo 3 do denominador. Aí a conta fica até mais fácil e o resultado é exatamente o mesmo.
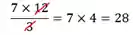
Divisão de Frações
Agora vamos ver sobre divisão de frações. Fica ligado, porque aqui as coisas podem sair do controle bem rápido.
Uma divisão de frações é algo do tipo:
A ideia agora é transformar essa operação em uma multiplicação. Para isso, vamos sempre lembrar da regrinha: multiplica a primeira fração pelo inverso da segunda. Com isso, essa continha aí de cima vai ficar assim:
Aí já podemos simplificar aquele 9 do numerador com o 3 do denominador, pra facilitar nossa vida.
Tranquilo, né? E se tivermos mais de duas frações dividindo?
Não tem muito segredo não, vamos só preservar a primeira fração e multiplicar pelo inverso de todas as outras.
E ainda podemos simplificar esse resultado final dividindo numerador e denominador por 3:
Bom, isso é o que temos pra hoje. Bora praticar pra deixar tudo isso bem enraizado na cabeça 😉