Introdução aos Números Complexos
Teoria
Motivação
FAAAAAAALA AÍ! Tudo bem?
Vou começar essa teoria te mostrando essa equação:
“Opa, opa, opa! É uma equação do segundo grau! Posso fazer Bháskara ou simplesmente isolar o ”
Você lembra que sempre que encontrávamos raízes de números negativos, dizíamos que não existiam soluções para a equação no conjunto dos números reais?
Pois é, os matemáticos se depararam com situações como estas, mas eles não aceitavam simplesmente dizer que não haveria solução no conjunto que eles trabalhavam, então eles fizeram o que sempre fazem: criam uma maneira de resolver!
Então assim surgiu o , que seria denotado por , dando início a um conjunto muito importante, que abrange inclusive o conjunto dos reais: o conjunto dos números complexos .
Agora finalmente podemos resolver:
Aleluia! Para você ter uma noção do quão importante esses caras são, pelo Teorema Fundamental da Álgebra, todo e qualquer polinômio de uma variável e de grau , tem raízes! Você pode não reparar, mas isso é muito forte na Matemática.
Representação cartesiana ou algébrica
Bom, vamos voltar ao número complexo que encontramos:
Perceba que temos duas opções: . Escolherei para começar, que eu vou escrever, por questão de notação, como:
Note que é a mesma coisa que escrever:
O número complexo é composto por uma parte real, que chamaremos de e uma parte imaginária, que chamaremos de , este acompanha o . Então no nosso caso, temos:
Esta é a representação cartesiana:
Onde e b são números reais e temos que:
Quando a parte real , dizemos que é um número imaginário puro, ou seja, só termo em .
O conjugado de um número complexo
Dado um número complexo
O conjugado dele é
Ou seja, só precisamos trocar o sinal da parte imaginária!
Exemplo:
O conjugado desse complexo será:
Viu só?
Representação Gráfica
Caaaaara, agora você vai ver que números complexos não são nada complexos! Apenas mais uma forma de escrever números! Vamos relembrar nosso plano cartesiano :
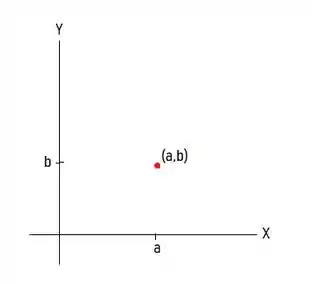
Nesse plano, está representado o ponto . Lembra disso?
A boa notícia é que podemos representar em um plano muito parecido com esse, apenas renomeando os eixos. Olha só:
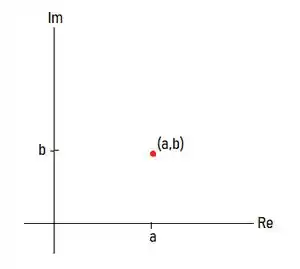
Sim, o some, a gente só representa a parte real no eixo real e representa a parte imaginária
no eixo imaginário. Esse novo plano é chamado de plano complexo de Argand-Gauss!
Olha só uns exemplos de complexos representados no plano:
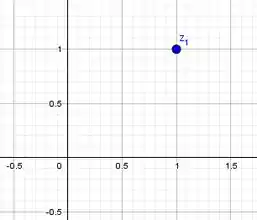
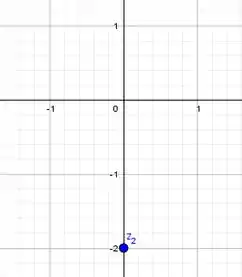
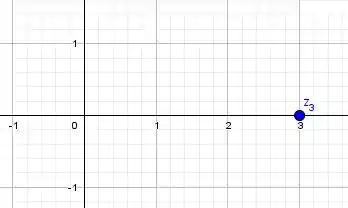
Simmmmm, um número real também está no conjunto dos complexos, afinal:
Representação trigonométrica
“Aff, Trigonometria nãooooo! Detesto senos e cossenos...”
Relaxa, essas coisas nos complexos são bem bonitinhas! Primeiro, vamos introduzir dois conceitos:
Vamos visualizar graficamente cada um desses conceitos. Começando pelo módulo, que chamei de :
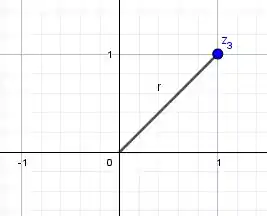
Perceba que temos ali um triângulo retângulo, e o módulo é justamente a hipotenusa desse triângulo.
Agora vamos visualizar graficamente o argumento :
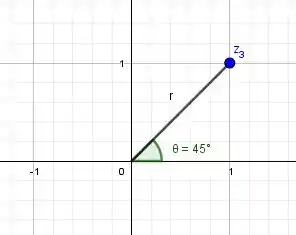
Perceba que o argumento o ângulo que o segmento e o eixo real.
Novamente, como temos um triângulo retângulo, podemos relacionar o argumento com os lados do triângulo. A relação é a seguinte:
A forma trigonométrica é:
Ou simplesmente escrevemos:
Onde .
No nosso exemplo, e . Então teremos:
Se você realizar essa multiplicação, verá que cairemos no mesmo complexo .
Representação polar
Essa representação é igual a trigonométrica, muitas vezes até são dadas como iguais. A única coisa que usamos aqui é que:
Então o nosso complexo :
Onde:
Então se representarmos como:
Exemplo completo
Represente graficamente, dê o conjugado, e represente na forma trigonométrica e polar o seguinte complexo:
Bom, representando graficamente:
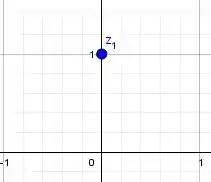
O conjugado será simplesmente trocando a parte imaginária pelo oposto:
Para a forma trigonométrica, podemos simplesmente olhar a figura e observar que temos um ângulo reto ali, assim:
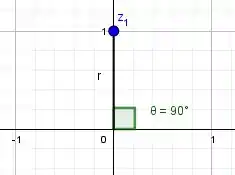
Porém, nem sempre será assim, então vamos calcular :
E isso não existe, então o certo é fazermos o limite:
Então precisamos pensar em ângulos de a que possuam tangente tendendo ao infinito:
Porém como o nosso complexo está na fronteira entre o primeiro e o segundo quadrante, ele tem que ser .
E calculando o módulo de :
Finalmente, a forma trigonométrica é:
Finalmente, vamos à forma polar, que é simplesmente escrever um complexo como
Onde e
Já sabemos que e
Espero que tenha curtido, bora pros exercícios!
O conjugado de um número complexo
Representação Gráfica
Representação trigonométrica
Representação polar
Exemplo completo
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Em cada um dos itens, indique a parte real, a parte imaginária e o módulo do número complexo. É um imaginário puro?
Passo 1
FAAAAAALA AÍ, chuchu! Beleza?!
Essa questão fala sobre números complexos (Jura?), mas especificamente sobre a parte real, a parte imaginária e o módulo de um complexo! Então, deixe-me refrescar sua memória quanto a isso!
Se temos um complexo da forma:
Segue que a parte real é:
Um caso especial é que se , então e dizemos que é um imaginário puro.
A parte imaginária é:
E o seu módulo é dado pela expressão:
Finalmente, bora começar!
Passo 2
Bom, a parte real é aquela que NÃO acompanha o :
E a parte imaginária é quem acompanha o :
Perceba que como , então esse complexo não é um imaginário puro!
Calculando o módulo:
Passo 3
Bom, a parte real é aquela que NÃO acompanha o :
E a parte imaginária é quem acompanha o :
Perceba que como , então esse complexo não é um imaginário puro!
Calculando o módulo:
Passo 4
Bom, a parte real é aquela que NÃO acompanha o :
E a parte imaginária é quem acompanha o :
Perceba que como , então esse complexo é um imaginário puro!
Calculando o módulo:
Passo 5
Bom, a parte real é aquela que NÃO acompanha o :
E a parte imaginária é quem acompanha o :
Perceba que como , então esse complexo não é um imaginário puro! Além disso, , então podemos dizer que é um número real.
Calculando o módulo:
Resposta
. Não é imaginário puro.
. Não é imaginário puro.
. É imaginário puro.
. Não é imaginário puro, é um número real.
Exercício Resolvido #2
Elaboração Própria
Dados os complexos a seguir, determine o módulo e o argumento dos respectivos, além de representa-los no plano complexo de Argand-Gauss.
Passo 1
Faaaaala aí, melhor aluno de Pré-Cálculo! Para resolver essa questão, vamos precisar lembrar da fórmula de módulo e argumento, mas não se preocupe, porque eu estou aqui para isso hahaha
Dado um complexo da forma:
Onde são reais, temos que:
E além disso:
E sua representação no plano Argand-Gauss:
Passo 2
Bora começar do começo!
Vamos começar representando esse complexo no gráfico, para que fique melhor a visualização:
Bom, para calcular o módulo, temos que:
Então:
Agora que achamos o módulo, vamos em busca da última coisa: o argumento!
Segue que:
Então os ângulos de a que possuem tangente igual a são:
Porém, repare que nosso argumento está no primeiro quadrante, já que ele é o ângulo entre o eixo real e o segmento da origem ao complexo.
Então .
Passo 3
Vamos começar representando esse complexo no gráfico, para que fique melhor a visualização:
Bom, para calcular o módulo, temos que:
Então:
Agora que achamos o módulo, vamos em busca da última coisa: o argumento!
Segue que:
Então os ângulos de a que possuem tangente igual a são:
Porém, repare que nosso argumento está no segundo quadrante, já que ele é o ângulo entre o eixo real e o segmento da origem ao complexo.
Então .
Resposta
Exercício Resolvido #3
Elaboração Própria
Escreva os seguintes números complexos na forma trigonométrica:
Passo 1
Bom, primeiro de tudo é saber escrever um complexo na forma trigonométrica. Dado um complexo:
Sua forma trigonométrica é:
Onde e . Bora começar!
Passo 2
Calculando seu módulo:
E agora vamos acha seu argumento:
Como isso não existe, precisamos calcular o limite:
Então, precisamos pensar quais ângulos de a que possuem tangente tendendo pro infinito. Esses são:
Porém, olhe a representação do nosso complexo no plano:
Então .
Agora que já temos nossos módulo e argumento, bora representação trigonometricamente o complexo:
Passo 3
Calculando seu módulo:
E agora vamos acha seu argumento:
Então, precisamos pensar quais ângulos de a que possuem tangente igual a . Esses são:
Porém, olhe a representação do nosso complexo no plano:
Portanto, .
Agora que já temos nossos módulo e argumento, bora representação trigonometricamente o complexo:
Passo 4
Calculando seu módulo:
E agora vamos acha seu argumento:
Então, precisamos pensar quais ângulos de a que possuem tangente igual a . Esses são:
Porém, olhe a representação do nosso complexo no plano:
Portanto, .
Agora que já temos nossos módulo e argumento, bora representação trigonometricamente o complexo:
Resposta
Exercício Resolvido #4
Elaboração Própria
Represente os seguintes números complexos na forma polar:
Passo 1
Bom, colocar complexos na forma polar é fazer:
Onde:
Então ele é equivalente a forma trigonométrica, só que aqui utilizamos a identidade de Euler:
Bora colocar a mão na massa!
Passo 2
Primeiramente, precisamos do seu módulo:
Agora vamos em busca do seu argumento:
Precisamos pensar nos ângulos de a que possuem tangente igual a . Eles são:
Porém, perceba que representando nosso complexo graficamente:
Então e a representação polar do complexo será:
Passo 3
Primeiramente, precisamos do seu módulo:
Agora vamos em busca do seu argumento:
Precisamos pensar nos ângulos de a que possuem tangente igual a . Eles são:
Porém, perceba que representando nosso complexo graficamente:
Então e a representação polar do complexo será:
Resposta
Exercício Resolvido #5
Elaboração Própria
Dado o complexo abaixo:
Determine:
.
A forma trigonométrica de e de .
A forma polar de e de .
Passo 1
Faaaala, meu raio de Sol! Bora começar do começo!
Opa! Surgiu finalmente um conjugado! Você lembra o que ele é?
Dado um complexo:
O conjugado será:
Bom, então no nosso caso:
Passo 2
Vamos começar calculando o primeiro módulo:
Agora vamos calcular o outro módulo:
Opa! Os dois são iguais!
Que bom, né? Pois tem que ser assim! Então se você encontrar módulos diferentes, volte e veja aonde você errou 😉
Passo 3
Bom, vamos começar achando . Sabemos que:
Precisamos pensar em ângulos de a que possuam tangente igual a :
Mas perceba que como a parte real é positiva e a parte imaginária também, então estamos no primeiro quadrante! Logo,
Agora vamos em busca de :
Precisamos pensar em ângulos de a que possuam tangente igual a :
Mas perceba que como a parte real é positiva e a parte imaginária é negativa, temos que estar no quarto quadrante! Logo, .
Perceba que:
Ou seja:
Essa relação vale sempre! De agora em diante você nem precisa calcular, basta usar essa relação!
Passo 4
A forma trigonométrica de e de .
A forma trigonométrica de um complexo do tipo é:
Onde:
Começando com . Já calculamos seu módulo e argumento, então:
Escrevendo na forma trigonométrica:
E agora vamos escrever na forma trigonométrica, sabendo que:
Escrevendo na forma trigonométrica:
Porém, lembre-se de que e . Então:
Passo 5
Finalmente, porém não menos importante, vamos ao último item:
A forma polar de e de .
Para você que ainda não tem essa forma gravada, olha só como ela é:
Onde:
Começando por , temos que e :
Agora escrevendo na forma polar o , sabendo que e :