Não existe nenhuma regra para soma ou subtração de raízes, por isso vamos resolver cada uma delas individualmente:

• Primeira

Vamos pensar em que número elevou ao quadrado (índice) para obter o valor do radicando 4.

Sabemos que se elevarmos 2 ao quadrado chegou exatamente em 4, ou seja:

Passo 2

• Segunda

Uma das propriedades diz que independente do índice, a raiz de 0, sempre vai ser 0:

Passo 3

• Terceira

Outra propriedade diz que se o radicando for 1, independente dado valor d índice o resultado sempre vai ser 1:

Agora que descobrimos o valor de cada uma individualmente, agora é só fazer a soma:

1. Se tivermos duas ou mais raízes se multiplicando de mesmo índice, podemos fazer uma raizona só, com o mesmo índice.

Na letra a, ambas são raízes quadradas, ou seja, podemos usar a regrinha:



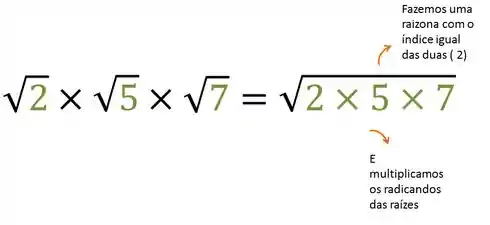
Agora é só fazer a multiplicação:

Pronto, essa é a nossa única raiz.·.

Passo 2

2. Vamos seguir a mesma ideia, agora temos o índice 12 nas duas raízes, assim podemos fazer uma raizona:

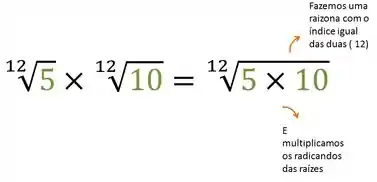
Agora é só multiplicar:

1. Para escrevermos numa só raiz a divisão, precisamos de índices iguais.

Nesse caso ambas são raízes quadradas e possuem índice 2. Assim, podemos transformar em uma única raizona com esse mesmo índice:



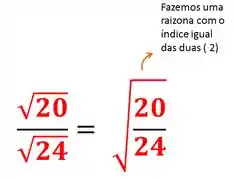
Essa divisão não é exata, PORÉEEM precisamos simplificar. Podemos dividir em cima e em baixo por 4, e teremos:

Prontinho, não temos mais simplificações e deixamos em uma raiz só.

Passo 2

2. Temos agora o mesmo índice 5, então novamente conseguimos fazer uma raizona:

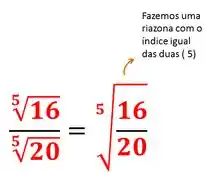
Agora é só fazer a simplificação, vamos simplificar por 4:

Prontinho, chegamos na nossa resposta.

Nesse exercício chegamos ao caso em que os índices são iguais, para resolver vamos multiplicar os radicandos e fazer uma raiz só, ou seja:

Como, temos o expoente do radicando igual ao índice da raiz, podemos “cancelar” eles, lembrando que 2 é par logo o resultado sai em módulo:

Assim, o resultado da nossa multiplicação é 6.

Dá uma olhada nessas raizes, ambas estão sendo multiplicadas por um número e têm índice 2 ( ou seja, estão elevado ao quadrado).

A idéia aqui é você sempre multiplicar raiz com raiz e número com número:

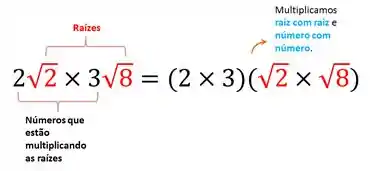
Agora podemos resolver separadammennte essas multiplicações e no final ssó mmultiplicamos os resultados.

Resolvendo a multiplicação entre os números :

Agora, vamos resolver a multiplicação entre as raizes :

Ambas raizes tem o mesmo índice 2, por isso podemos usar nossa regrinha. Vamos juntar as duas raizes numa só comm o mesmo índice, e dentro dela tem os radicandos se multiplicando :

Para resolver essa raiz, vamos pensar em que número foi elevado ao qquadrado ( índice ) para obtermos 16 ?

Sabemos que é o 4. Por que .

Assim, temos que :

Agora, vamos multiplicar oss nossos resultados

Essas raízes possuem índices iguais, assim podemos usar nossa regrinha.

Podemos fazer uma raiz só com o mesmo índice e dividir os radicandos, ou seja:

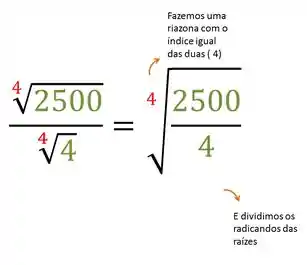
Agora é só fazer essa divisão, depois resolvemos a raiz.

Agora para resolver, vamos pensar em que número foi elevado á quarta potência para termos 625.

Vamos testar o número 5:

Assim, temos:

Para resolvermos esse exercício, vamos fazer a mesma coisa que fizemos para a multiplicação, número inteiro com número inteiro e raiz com raiz

Podemos imaginar como duas frações:

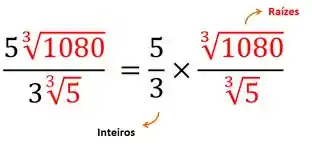
Vamos deixar os inteiros de lado por um momento e vamos resolver as raízes, elas têm o mesmo índice 3, assim aprendemos que podemos fazer um raizona só, com o mesmo índice e dividir os radicando:

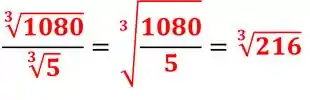
Agora para resolver essa raiz, temos que pensar em qual número que foi elevado ao cubo, para obter 216. Vamos testar o seis:

Pronto, sabemos que:

Agora só vamos resolver a multiplicação:

Vamos montar o enunciado, temos que a metade da raiz quadrada de um número é 5. Metade é dividir por 2, e basta igualarmos a 5 :

Podemos multiplicar os dois lados dessa equação por 2, ssimplismente passar o 2 que esttá dividindo para o outro lado da equação multiplicado :

Que resulta :

Agora vamos lembrar que a raiz é o inverso da potenciação, ou seja, se queremos saber que raiz quadrada dá 10, podemos simplesmente elevar o 10 ao quadrado :

Sabemos que

Logo achamos o número que procurávamos.