Racionalização de Denominadores
Produzido por Marcelo LuizTeoria
A racionalização de denominadores serve para transformar uma fração com denominador irracional em uma fração equivalente com denominador racional.
Assim:
Como Fazer Racionalização?
A racionalização, nada mais é do que você pegar a fração com o denominador contendo raízes, e multiplicar o numerador e denominador por um fator racionalizante, também chamado de conjugado do número.
Esse fator vai fazer com que a nossa fração passe a ter um denominador sem raízes!
Por exemplo:
Nesse caso o fator racionalizante é
No vídeo abaixo a gente te explica passo a passo como fazer a racionalização! 👇
Ou, se você preferir, continua comigo no textinho! 👇
Existem três casos diferentes que nos ajudam a escolher o melhor fator racionalizante. Bora dar uma conferida neles?
Caso 1 - Raiz quadrada no denominador
Nesse primeiro caso vamos ver como fazer a racionalização quando temos o denominador com uma raiz quadrada.
Como por exemplo:
O fator racionalizante nesse caso sempre será a própria raiz contida no denominador, nesse caso,
Então fazemos:
Prontinho!
Caso 2 - Raiz de índice diferente que 2 no denominador
Nesse caso, vamos ter uma fração onde o denominador é parecido com:
O fator racionalizante será:
Exemplo:
Então podemos resolver fazendo:
Caso 3 - Denominador com Soma ou Subtração
Nesse caso, deve existir pelo menos uma raiz no denominador. Então temos as seguintes possibilidades:
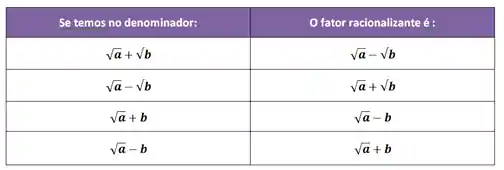
Exemplo:
Como temos
Agora é só multiplicar o fator no denominador e numerador da nossa fração
Precisamos resolver esse produto no denominador:
Agora voltamos para fração:
Aweee!
Agora que você já esta sacando tudo sobre Racionalização de Denominadores, bora praticar com exercícios?!