Plano Cartesiano e Funções
Produzido por Marcelo LuizTeoria
Introdução
Você já se perguntou como funciona a localização de um gps ou como um marinheiro consegue se guiar em mar aberto?
A verdade é que existem muitos conceitos e equipamentos por trás disso, mas nos dois casos há uma coisa em comum...
Ambos precisam do Plano Cartesiano.
Mas e quando falamos de matemática, pra que serve essa coisa??

(Jack Sparrow com dúvida porque só usa o plano cartesiano para navegar)
A resposta para essa pergunta é tão grande que é até difícil de falar.
Mas aí vai algumas de suas utilidades:
- Achar pontos no plano e espaço.
- Determinar áreas de figuras geométricas.
- Estudar comportamento de fun�es diversas.
Como é o Plano Cartesiano
Beleza, mas como é formado o plano cartesiano?
Ele é formado por dois eixos ou duas retas perpendiculares, ou seja, formam um ângulo de entre si.
A reta horizontal é chamada de Abscissas e a reta vertical é chamada de Ordenadas.
Obs: Na maioria dos casos, não encontramos os nomes dos eixos com abscissas ou ordenadas, é comum representar as abscissas como e as ordenadas como .
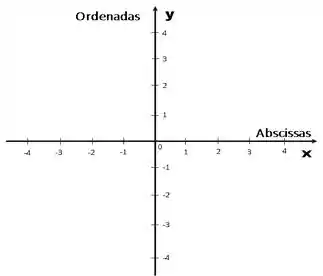
Observe que os eixos se cruzam no ponto em e .
Quadrantes
Se analisarmos a disposição dos eixos, percebemos que o plano fica dividido em quatro regiões diferente...
Chamamos essas regiões de Quadrantes:
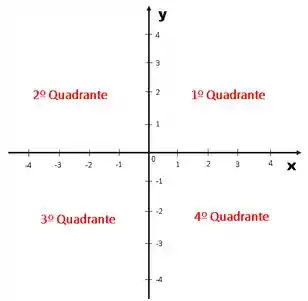
Relações dos valores dos Quadrantes:
- 1º Quadrante e ;
- 2º Quadrante e ;
- 3º Quadrante e ;
- 4º Quadrante e .
Pontos no Plano Cartesiano
Agora que vimos um pouco mais sobre o plano cartesiano, podemos começar encontrar pontos no plano.
Mas o que seria isso?
Imagine que o um navio está à deriva no mar e o capitão precisa indicar o exato ponto onde o navio se encontra para que o resgate seja preciso.
Para isso, ele deve indicar sua latitude e longitude, que pode ser considerado como ponto de abscissas e ordenas.
É comum chamar um ponto no gráfico de Par Ordenado. Esse par é dado pelo conjunto do ponto de abscissas com o ponto da ordenada.
Onde:
Abscissas.
Ordenadas.
Exemplo
O que fazer se nos pedirem para encontrar o ponto no plano?
Já sabemos que o ponto se refere ao eixo e que o ponto se refere ao eixo .
Dessa forma, temos:
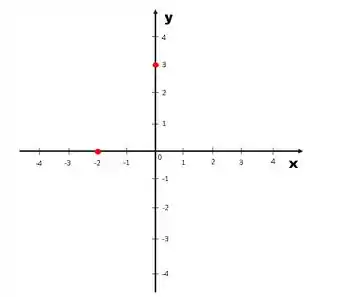
Para achar a intersecção dos pontos, basta traçar duas perpendiculares aos eixos dos pontos e encontrar o ponto onde elas se cruzam:
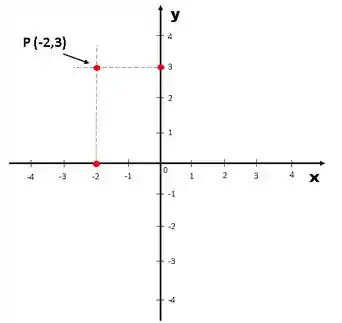
E tá pronto!!
Bora fazer uns exercícios de fixação!?
Como é o Plano Cartesiano
Quadrantes
Pontos no Plano Cartesiano
Exemplo
Exercícios Resolvidos
Exercício Resolvido #1
Autoria própria.
Maria fez um mapa da sua escola utilizando o plano cartesiano e marcou o ponto exato em que cada lugar estava:
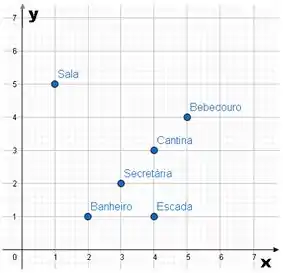
Qual é a coordenada que representa o bebedouro?
Passo 1
Para indicar a coordenada exata do bebedouro precisamos indica seu par ordenado, dado pela coordenada do eixo com a coordenada do eixo .
Em , o bebedouro está cinco unidades para frente.
Em , o bebedouro está quatro unidades para cima.
Portanto, o ponto é dado por .
Resposta
.
Exercício Resolvido #2
Autoria própria.
Indique o quadrante em que cada ponto se encontra:
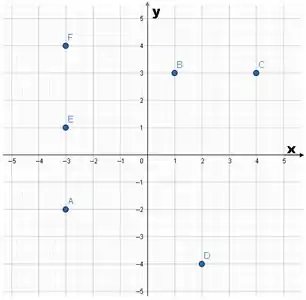
Passo 1
Os quatro quadrantes são divididos da seguinte forma:
- 1º Quadrante e ;
- 2º Quadrante e ;
- 3º Quadrante e ;
- 4º Quadrante e .
Os pontos e possuem coordenadas e respectivamente.
Como e são positivos, os dois pertencem ao 1º quadrante.
Os pontos e possuem coordenadas e respectivamente.
Como e , os dois possuem ao 2º quadrante.
O ponto possui coordenada .
Como e são negativos, o ponto pertence ao 3º quadrante.
O ponto possui coordenada .
Como e , o ponto pertence ao 4º quadrante.
Resposta
1º Quadrante - e .
2º Quadrante - e .
3º Quadrante - .
4º Quadrante - .
Exercício Resolvido #3
Autoria própria.
Analise a imagem abaixo e escolha a alternativa FALSA:
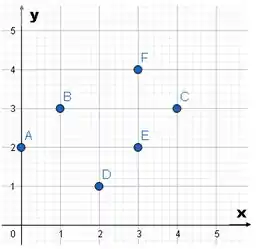
a) O ponto não tem deslocamento no eixo .
b) Os pontos e estão equidistantes do ponto .
c) O ponto é o que tem o maior deslocamento em .
d) O ponto é equidistante aos pontos e .
Passo 1
Vamos analisar cada alternativa separadamente...
Letra a)
Verdadeira!
O ponto a é dado pelo par ordenado , ou seja, não tem deslocamento em .
Letra b)
Verdadeira!
A distância de para e de para , são hipotenusas de triângulos equivalentes, tendo cada um de seus catetos com unidade de comprimento.
Letra c)
Verdadeira!
O ponto é dado pelo par ordenado . Como nenhum outro ponto atinge unidades em , ele é o que tem o maior deslocamento nesse eixo.
Letra d)
Falsa!
Para se deslocar de para é necessário deslocar-se unidades no eixo e no eixo .
Já de para é necessário deslocar-se unidades no eixo e unidades no eixo .
Portanto, as distâncias não são equivalentes.
Resposta
Alternativa d).
Exercício Resolvido #4
Autoria própria.
Calcule o perímetro do triângulo dado pelos vértices , , .
Passo 1
Podemos representar o triângulo dado a partir dos vértices como:
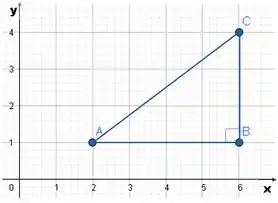
De até temos unidades.
De até temos unidades.
Como trata-se de um triângulo retângulo, podemos aplicar Pitágoras para descobrir o valor da hipotenusa.
Passo 2
Para saber o perímetro total, basta somarmos os valores de todos os lados.
Resposta
Unidades.
Exercício Resolvido #5
Autoria própria.
Um triângulo tem seus vértices definidos em , e . Qual é o par ordenado que define o baricentro desse triângulo?
Passo 1
Nesse exercício não precisamos nem imaginar como seria esse triângulo, basta aplicar a fórmula do baricentro.
Para , temos:
Para , temos:
Resposta
.
Exercício Resolvido #6
Autoria própria.
Encontre a área da figura dada pelos pontos , , e .
Passo 1
Podemos representar esta figura no plano cartesiano como:
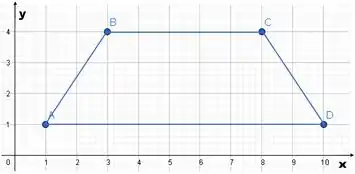
Os pontos formam um trapézio.
Sabendo que a área do trapézio é dada por , sendo:
Base maior.
base menor
Altura
Podemos calcular sua área analisando o plano.
Aplicando esses valores na fórmula da área do trapézio, temos:
Como a unidade dos eixos não está definida, dizemos que a unidades de área.
Resposta
.
Exercício Resolvido #7
(PM Pará 2012).
Os pontos , e são vértices de um triângulo retângulo. A área desse triângulo é:
a) 5 u.a
b) 6 u.a
c) 7 u.a
d) 8 u.a
e) 9 u.a
Passo 1
Podemos representar esse triângulo como:
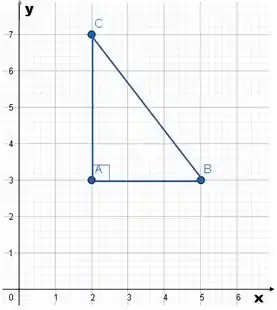
A área do triângulo é dada por:
Onde,
Área do triângulo.
Base do triângulo.
Altura do triângulo.
No triângulo dado, é a base e vale unidades, é a altura e vale unidades. Portanto, podemos calcular a área a partir dessas duas medidas.
Resposta
Alternativa b).
Exercício Resolvido #8
Autoria própria.
Calcule a distância entre os pontos abaixo:
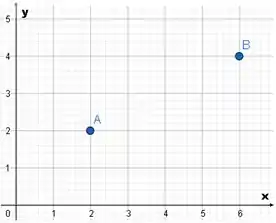
Passo 1
Queremos saber a distância entre os pontos e .
Perceba que se traçarmos um triângulo com o último vértice no ponto , teremos um triângulo onde a hipotenusa será a distância entre e .=
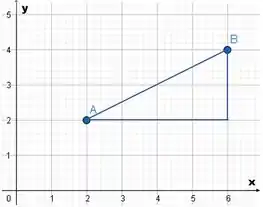
Assim, temos que:
Fatorando, temos que:
Resposta
.