Teoria
Introdução
Fala aí, tudo certinho!?
Nesse tópico vamos falar sobre um assunto que está muito presente no nosso cotidiano, a Porcentagem.

Vemos com frequência nas vitrines das lojas anúncios de liquidações com , , ... Sabemos que isso representa uma economia para nosso bolso, mas o que será que isso realmente quer dizer?
O que significa Porcentagem?
Bom, para que haja porcentagem, primeiramente deve haver uma grandeza inicial que representa de algo.
Dessa forma, ao compararmos uma segunda grandeza com a grandeza inicial, achamos a porcentagem de uma em relação a outra.

Deu uma bugada aí? Relaxa que com um exemplo tudo fica mais fácil...
Aplicação
Spoiler: Quando calcularmos porcentagem usamos basicamente Regra de 3.
Olhe esse exemplo:
Uma sala de aula tem ao todo alunos, quantas meninas há na sala sabendo que a porcentagem de menino é de ?
O problema nos dá a quantidade total de alunos na sala, a porcentagem referente a quantidade de meninos e pede para calcularmos o número total de meninas.
Olhe essa tabelinha:
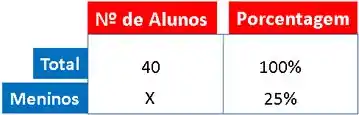
Neste caso alunos representa dos alunos da sala.
Beleza, pergunta para você agora: Você já viu algo parecido com isso em algum lugar?? (olha o Spoiler...)
REGRA DE 3!!!
Precisamos aplicar a regra de 3 para acharmos a quantidade de meninos, e como as grandezas são diretamente proporcionais, basta multiplicarmos cruzado:
Ok, já encontramos o número de meninos através da porcentagem que nos foi dada, mas o problema pediu o número de meninas, logo precisamos fazer uma continha de subtração apenas:
E tá pronto, há um total de 30 meninas na sala.
Se liga no MACETE
Se você é do tipo que adora um macete, essa aqui é especialmente para você
Também podemos ver a porcentagem como e isso é .
Tá, mas o que isso quer dizer?
Quer dizer que os do problema anterior é o mesmo que e isso é .

Ou seja, para encontrar quanto vale de alunos basta fazer:
Sacou!?
Vamos pensar você quer comprar uma roupa de 70 reais, mas ai tu descobre que ela está com de desconto, qual o valor desse desconto?
Usando o macete que temos é que
Como queremos saber o valor desse desconto (, vamos calcular de 70, ou:
Ou seja, a roupa vai ter um desconto de .
Outros problemas envolvendo porcentagem
Acabamos de ver como resolver problemas simples envolvendo porcentagem.
Mas o que fazer quando queremos achar uma porcentagem dentro de outra porcentagem?

Se liga nesse exemplo:
O quintal de uma casa equivale à do terreno total e o proprietário gostaria de construir uma área de churrasqueira equivalente à do quintal. Qual é a porcentagem da área de churrasqueira em relação ao terreno todo?
Aplicação
Nesse problema temos que a área de churrasqueira vale de da área total.
Como vimos anteriormente, e , logo para saber quanto é de precisamos multiplicar as duas porcentagens:
Beleza, mas o que problema pergunta pra gente é a porcentagem, e agora?
Moleza, basta multiplicar por !
A área de churrasqueira equivale à do total do terreno.
Pronto, agora também sabemos resolver esses problemas malucos que dão um nó na nossa cabeça.
E aí meu querido, bora fazer uns exercícios?