Soma de Decimais e Subtração de Decimais
Produzido por Marcelo LuizTeoria
Fala ai! Bem vindo ao RespondeAi! Aqui ensinamos engenheiros, químicos, matemáticos e quem mais estiver precisando sobre Cálculo, Física, Química e outras matérias. Gostamos de construir os fundamentos para facilitar a compreensão dos assuntos. Então vamos relembrar soma e subtração de decimais nessa página através de alguns exemplos, que tal?
Quando falamos de números, existe uma diferença entre números inteiros e números decimais. Olhe a seguir:
Números inteiros:
- 1
- 3
- 5
Números decimais:
- 1,25
- 3,3...
- 5,978
Então já podemos ver a diferença entre eles, os números inteiros não contém nenhum valor depois da virgula, e por isso representam valores inteiros, porém números decimais tem valores depois da virgula, e representam valores fracionários.
O interessante é que assim como fazemos com os números inteiros, nós podemos executar operações entre os números decimais. Hoje estaremos interessados em aprender sobre a soma de números decimais e subtração de números decimais.
Os números decimais, apresentam duas partes, a parte inteira antes da virgula, e parte decimal. Essas duas partes são sempre separadas por uma vírgula.
Confere essa tabela de exemplo:
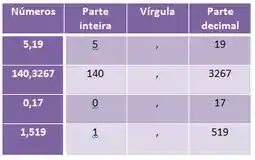
Na parte decimal de cada número, encontramos as casas decimais desse número.
O número
Soma de números decimais
Imagina que você corta uma pizza em 4 pedaços, então podemos dizer que cada pedaço representa 0,25 da pizza. Eu estou usando um número decimal para representar
Então caso você coma dois pedaços dessa pizza que você cortou, você teria comido:
Você teria comido metade da pizza e
E se quiséssemos somar dois números decimais, mas que possuíssem diferentes números de casas decimais? Por exemplo:
Para resolver esse problema e calcular essa soma, teríamos que alinhas os números pela vírgula, e na hora de resolver, colocar "0" nas colunas vazias:
Alinhando pela vírgula:

Adicionando os zeros:

E agora podemos somar normalmente:
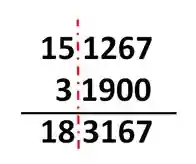
Aqui podemos até fingir que a vírgula não existe por alguns momentos, desde que a gente volte a representar ela, com o número correto de casas decimais, quando acabar a operação.
Então:
Subtração de números decimais
Showw, agora que já estamos sabendo o que são os números decimais, e já sabemos como somar decimais, imagina a seguinte situação... Você foi ao mercado com
A nossa ideia natural é subtrair do valor que eu tenho, o valor que tenho que pagar:
Novamente, precisamos alinhar conforme a vírgula, para garantir o alinhamento correto das casas decimais, em caso de subtração entre números com número de casas decimais diferentes adicionar os "0" necessários.
No nosso exemplo, ambos os números tem o mesmo número de casas decimais, então somente precisamos alinhá-los conforme a vírgula:
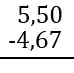
Podemos fazer os cálculos como se a vírgula não existisse, então fazendo a subtração
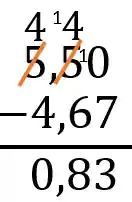
Agora que tal resolvermos um exercício de subtração de números decimais? Tenta fazer você ai primeiro, e depois confira a nossa solução:
Exercício de Subtração de Decimais
Resolva a subtração:
Passo 1
Nas nossas resoluções Passo a Passo, que estão em todos os exercícios do site e que detalham todas as etapas do raciocínio para a resolução da questão, você encontra o exercício resolvido com carinho pelo nosso time de Experts e pensado especialmente para você.
No nosso exercício o Passo 1, será montar a continha de subtração, como estamos acostumados a fazer, mas alinhando os números conforme a vírgula:
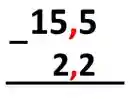
Passo 2
Agora, fingimos que a vírgula não existe, e substituímos ela "mentalmente", por uma linha que separa, a parte inteira da parte decimal dos números:
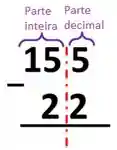
Passo 3
Subtraímos normalmente
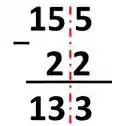
Passo 4
Recolocando a vírgula, no lugar correto, seguindo nossa linha "mental" que separa a parte inteira da parte decimal, temos que:
Resposta
Shoow, se você ainda tiver dúvidas, em todos os tópicos que abordamos existe uma lista de exercícios, que são ordenados em ordem crescente de dificuldade, onde muitos contam também com resolução em vídeo! Confere lá!