Equação de círculos, hipérboles e parábolas
Produzido por Erick PinhoTeoria
Introdução
Fala, galera! Agora vamos aprender um pouco sobre as seções cônicas, que nada mais são que aquelas figuras que a gente já conhece: Circunferência, Elipse, Hipérbole e Parábola.
Mas aí você me pergunta: “Por que raios isso é chamado de cônicas?”
Faz de contas que a gente tem dois cones unidos pelos vértices, tipo uma ampulheta, e vamos fatiar estes cones em quatro posições distintas, formando as quatro figuras que a gente viu. Vamos ver como que a gente pode fazer isso explicando bem uma por uma.
Circunferência
É a seção horizontal, ou seja, se a gente cortar o cone com um plano horizontal a parte do cone que tocou o plano é uma circunferência, como na figura:
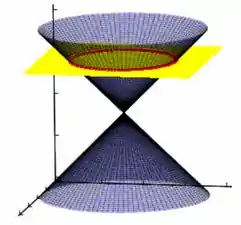
A equação geral da circunferência é dada por:
Sendo o ponto que representa o centro e o raio dessa circunferência. Tipo assim:
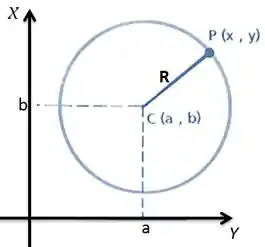
Daí, se a circunferência estiver centrada na origem, ou seja, a equação da circunferência será dada por:
Elipse
Uma elipse é meio que uma circunferência esticada em um dos eixos. Esse “esticamento” é feito a partir da rotação do plano que corta o cone em um pequeno ângulo, como na figura abaixo:
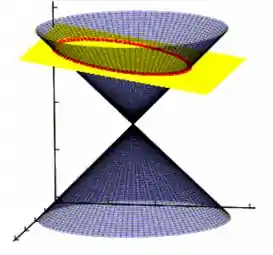
A equação da elipse é dada por:
Sendo novamente o centro da circunferência e o tamanho dos semieixos horizontais e verticais respectivamente da elipse.
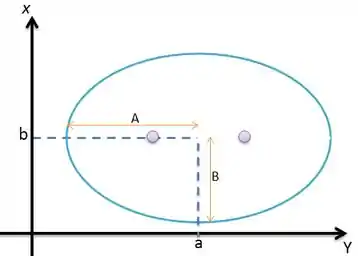
Obs: Se , teremos uma elipse “deitada”, ou seja, o eixo maior da elipse é paralelo ao eixo . Já no caso de , teremos uma elipse “em pé”, ou seja, o eixo maior da elipse é paralelo ao eixo . Se teremos uma circunferência. :D
Bizus de como identificar uma elipse:
Existem algumas formas de se escrever a equação de uma elipse, porém para identificar que é uma elipse temos que SEMPRE transformar a equação dada em algo do tipo .
- Parábola: Sempre um OU o OU o estará ao quadrado e não os dois.
- Elipse: Os coeficientes que multiplicam e são diferentes mas sempre positivos.
- Circunferência: Os coeficientes que multiplicam e são iguais e sempre positivos.
- Hipérbole: Um dos coeficientes que multiplicam OU são negativos, mas não os dois.
Pra chegar na equação da elipse, devemos ter o lado direito da igualdade igual a 1, então bora dividir os dois lados por 36.
Que é uma elipse de semieixo maior e semieixo menor .
Ah, aqui podemos substituir o por pra ficar mais a cara da equação que aprendemos.
Elevando os dois lados ao quadrado, teremos:
Passando tudo pra um lado só, teremos:
Aí que vem o pulo do gato. Podemos somar 2 os dois lados e teremos...
Mas como temos que deixar o lado direito da igualdade como 1 , devemos dividir os dois lados por 2, logo:
Ou melhor:
E pra esboçar, vamos ter uma elipse de , deslocada no eixo na posição .
Mas tá, então, vamos ter uma elipse completa com essas características né?
Só que não! Lááá em cima teve um passo em que a gente viu que a gente passou de para . Se a gente tirasse a raiz de novo dessa segunda expressão nós teríamos:
Aí sim, essa expressão nos daria uma elipse completa, porém o que o enunciado nos deu só representa a parte positiva de , logo o nosso gráfico será:
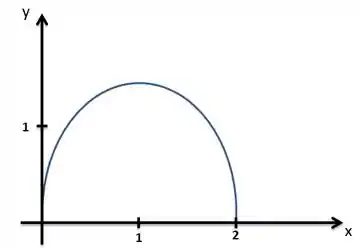
Parábola
A parábola é uma curva que a gente já conhece melhor desde o ensino fundamental que é a curva de uma equação de segundo grau, certo? Ela nada mais nada menos é que um corte no cone feito da seguinte forma:
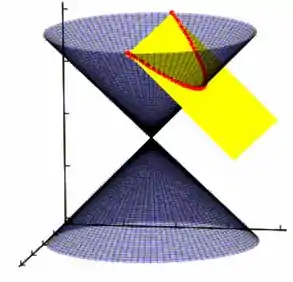
A equação das parábola é bem simples, e como falei, a gente já sabe bem como elas são escritas desde o ensino fundamental, as equações do 2° grau. A parada é que aqui também poderemos escrevê-las deitadas. Saca só!
Equação Geral para uma parábola “em pé”:
Tá, mas como vou desenhar a parábola a partir desta equação?
Aqui a gente vai fazer um sisteminha , onde os nossos coeficientes serão , [confia em mim]:
Sendo a posição do vértice da parábola e uma característica da parábola, (que aqui não vamos abordar muito, utilizaremos apenas para achar os valores de ).
Se a parábola estará com concavidade voltada para cima, se estará com a concavidade voltada para baixo, como mostrado nas figuras da esquerda e da direita respectivamente.
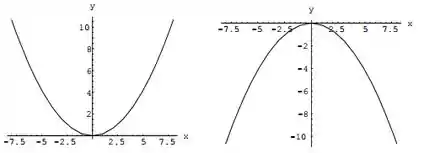
Equação Geral para uma parábola “deitada”:
Daí, teremos que:
Com as mesmas especificações dadas para o caso de parábola “em pé”.
Nesse caso, que se a parábola terá concavidade voltada para direita, e se a parábola estará voltada para a esquerda, como na figura abaixo:
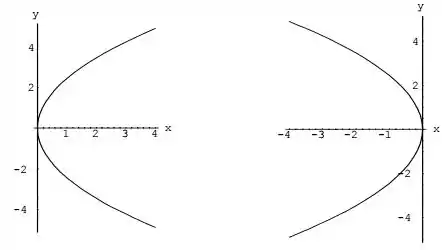
Um exemplo de como fazemos isso? Se liga aí!
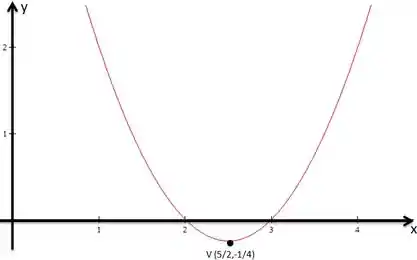
Plotar o gráfico da função .
A gente já sabe que pode substituir o por , né?
Daí aqui temos que:
Show?
Agora utilizamos o sisteminha lá:
Logo, .
Logo,
Logo,
Ah, também podemos ver que essa expressão tem duas raízes, . Para nos ajudar no esboço do gráfico podemos representar essas raízes também. Logo o gráfico será algo do tipo:
Hipérbole
A hipérbole talvez seja o gráfico que desses você menos ouviu falar. Ela é o corte do cone dado na seguinte posição:
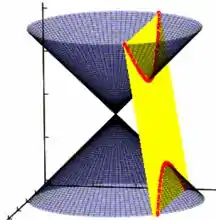
Como vimos aí, agora o plano corta duas vezes o cone em cima e embaixo.
A equação da hipérbole é bem parecida com a da elipse, com apenas um detalhe, uma das partes tem sinal de menos, ou seja:
Ou
No 1° caso, teremos uma hipérbole centrada no eixo horizontal, ou seja, a expressão que contém o é positiva.
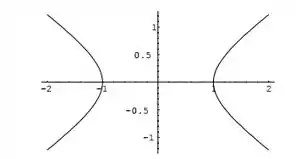
No 2° caso, teremos uma hipérbole centrada num eixo vertical, ou seja, a expressão que contém o é positiva.
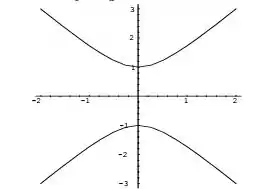
Tá, mas como é que eu vou esboçar essas hipérboles?
Simples!
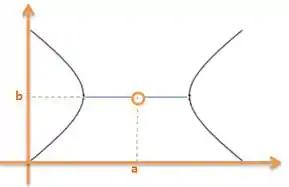
Após aquela equação montada vamos ter o centro da hipérbole no ponto . Ah, o centro é exatamente a metade da distância entre os vértices das duas folhas da hipérbole.
Se a hipérbole for do tipo centrada no eixo horizontal, ou seja, você vai pegar o ponto e andar pra esquerda e pra direita, de forma que os vértices serão em se mantendo na posição de
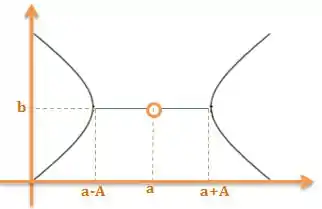
Logo os vértices serão .
Já para as hipérboles centradas na vertical a parada será o contrário. Elas também serão centradas em , porém seus vértices serão no eixo vertical, dado por:
Bizu dos bizus: Como que figura representa a minha equação:
E é isso aí, pessoal! Oh, nos exercícios vou mostrar melhor como tudo isso é cobrado. #PartiuPassar.
![]()
Circunferência
Elipse
Parábola
Hipérbole
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Esboce o gráfico da função:
Passo 1
A primeira coisa que a gente faz é mudar esse pra , certo? Certo!
Daí ficaremos com:
Vamos elevar os dois lados ao quadrado e ficaremos com:
MAS TOMA CUIDADO! Só existe função para , pois não existe função para raiz de números negativos, logo só teremos a parte do gráfico onde o , ou seja, acima do eixo
Passo 2
Continuando aqui teremos:
Dando aquele pulo do gato, somando e subtraindo 4, teremos:
Opa, chegamos na equação de uma hipérbole de centro com e centrada no eixo
Desta forma,como os vértices devem estar no eixo horizontal, eles estarão nas posições . Logo, nossa hipérbole será algo do tipo:
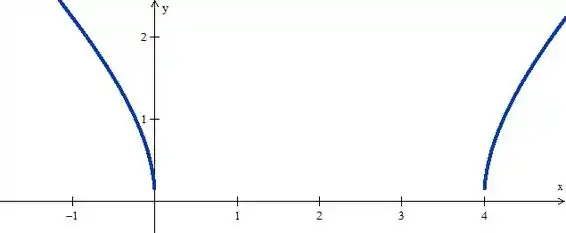
Resposta
Dada na resolução.
Exercício Resolvido #2
Elaboração Própria
Esboce o gráfico da função:
Passo 1
Opa, temos uma função composta! Devemos analisar as duas partes da equação. Primeiro, claro, chamando o de teremos:
Na primeira parte:
Elevando os dois lados ao quadrado, teremos:
Mas toma cuidado na raiz, como sabemos, temos somente a parte positiva do gráfico, sendo o resultado da raiz quadrada sempre , logo:
Nosso gráfico será esboçado a partir da reta . :D
Passo 2
Ajeitando a nossa equação, teremos:
Isso é exatamente a equação da circunferência, que é dada por:
Logo, teremos uma circunferência centrada em e de raio .
Relembrando:
- Para valores acima da reta .
- No intervalo .
- Para o resto da reta, ou seja, no intervalo teremos .
Logo o nosso gráfico será:
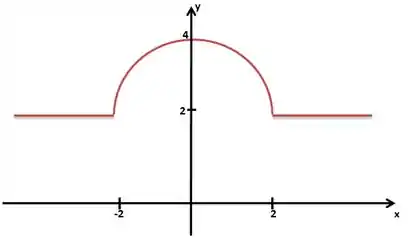
Resposta
Dada na resolução.
Exercício Resolvido #3
Elaboração Própria
Esboce o gráfico da função:
Passo 1
Como sempre, vamos chamar o nosso .
O diferente dessa questão é que para qualquer valor de existirá resultado para essa raiz quadrada pois esse resultado será SEMPRE maior ou igual a zero.
Vamos ver para quais valores a nossa função é positiva e quais ela é negativa. Pois:
Para os valores de positivos teremos que :
Já para os valores negativos de teremos :
Passo 2
Fazendo o estudo do sinal, teremos:
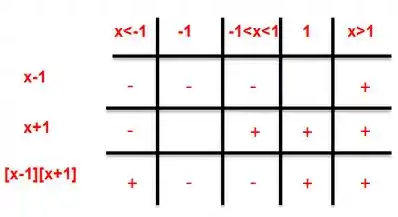
Logo, vemos que:
Passo 3
Resolvendo a equação para o intervalo [I], teremos:
Logo, a gente vê que para o intervalo [I] teremos uma hipérbole centrada em e vértice . Mas lembrando... Só para valores de por causa da raiz quadrada lá que só nos da valores positivos! :D
Agora resolvendo a equação para o intervalo [II], teremos:
Temos uma circunferência de raio , centrada na origem. Logo o nosso gráfico será:
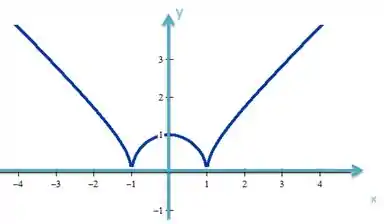
Resposta
Dada na resolução.