Geometria - Perímetro, Área e Volume
Produzido por Erick PinhoTeoria
Introdução
Chegou a hora de falar de perímetro, área, volume e as principais fórmulas relacionadas. Não vamos falar aqui da origem dessas fórmulas, deixaremos o assunto para quando estudarmos Cálculo.
O conceito de Área
Muito bem, vamos falar do que é área. O conceito de área é muito empírico, ou seja, muita gente sabe o que é, mas pode encontrar dificuldade na hora de definir com palavras.
O conceito por trás da área está ligado às dimensões. O nosso mundo é composto por três dimensões espaciais: o comprimento, largura e altura.
Quando falamos de área, estamos tratando somente de das dimensões, ou porque o espaço em estudo não inclui essa dimensão, ou então ela é desprezível ou não é de interesse.
Dessa maneira, podemos interpretar a área de determinado objeto como a quantidade de espaço bidimensional, ou a quantidade de espaço plano.
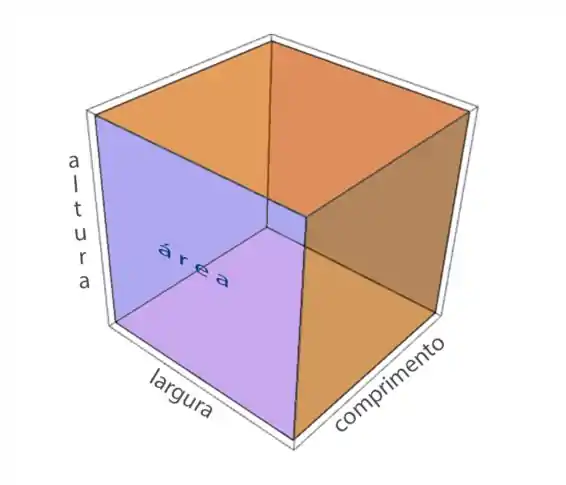
Para mensurar essa “quantidade” de espaço plano chamada área, fazemos como é recorrente: comparamos com outra medida.
Isso significa que medimos a área usando unidades com valores padronizados e muito bem determinados.
É comum encontrar área medida no Sistema Internacional de Unidades, em metro quadrado (m²). Um metro quadrado nada mais é que um quadradão de m de comprimento por metro de largura.
Dizer que um terreno tem m² é o mesmo que afirmar que caberiam quadradões de m² nele. Medir é comparar.
Principais fórmulas de área
Como falamos, a área é a quantidade de espaço plano e existem diversas formas planas com diferentes fórmulas para o cálculo da área a partir de suas dimensões.
Começamos com o clássico, o retângulo. A área de um retângulo é a base, ou comprimento vezes a altura :
\s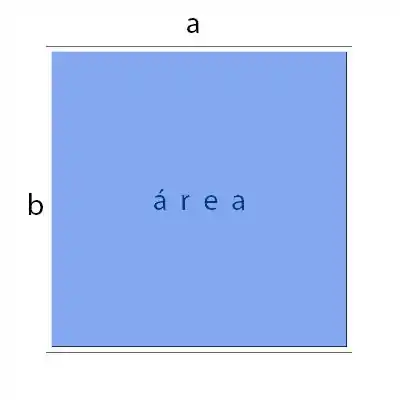
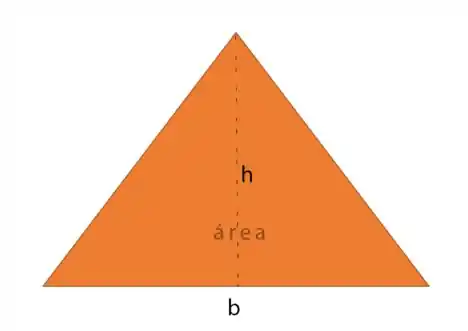
A área do triângulo, tão popular nos tipos de trigonometria, é definida pela base vezes a altura dividida por !
Para o trapézio, a área será a Base maior mais a base menor vezes a altura dividida por dois (ufa!):
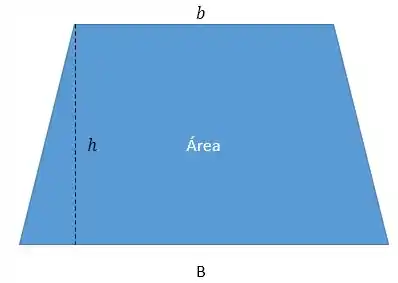
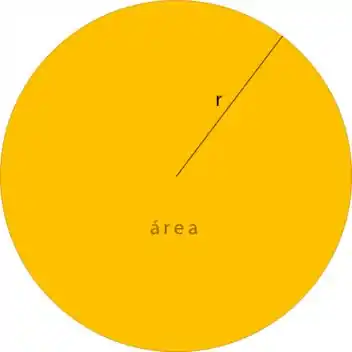
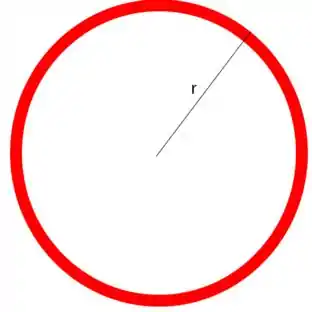
Já o círculo tem área igual a vezes o quadrado de seu raio :
Perímetro
O perímetro é ainda mais simples que a área. Só possui uma dimensão e é justamente o comprimento da linha de contorno do objeto. Em geral, o perímetro é a soma do comprimento dos lados da forma plana. Para o retângulo:
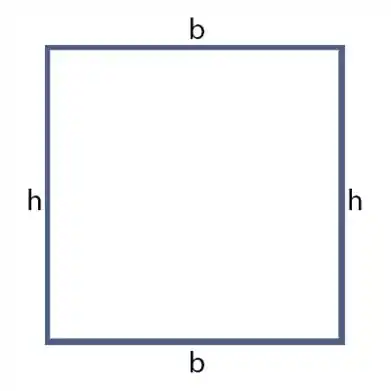
No triângulo:
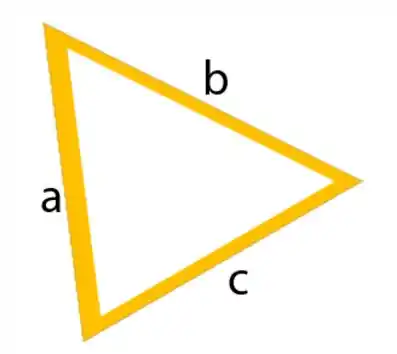
Já no círculo, o perímetro é comprimento da circunferência e igual a duas vezes vezes o raio:
Volume e principais fórmulas
Enquanto a área só trata de duas dimensões, o volume vai em frente e pega as três dimensões logo de uma vez. Para ele, a unidade no sistema internacional de unidades é metro cubico m³, um cubo com um metro de comprimento por um metro de largura, por um metro de altura.
Existem vários sólidos importantes que você precisa saber como calcular o volume, então vamos ver tudo com atenção!
O paralelepípedo tem volume igual ao produto do seu comprimento , largura e altura :
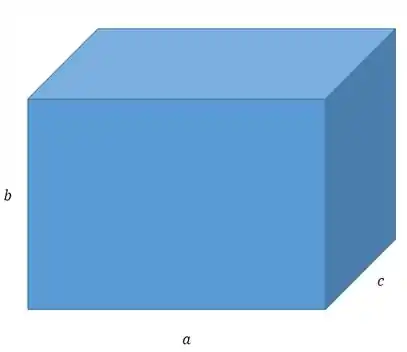
Vale lembrar que o cubo nada mais é que um paralelepípedo de lados iguais.
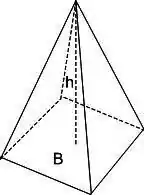
A pirâmide tem volume igual a área da base vezes a altura dividida por :
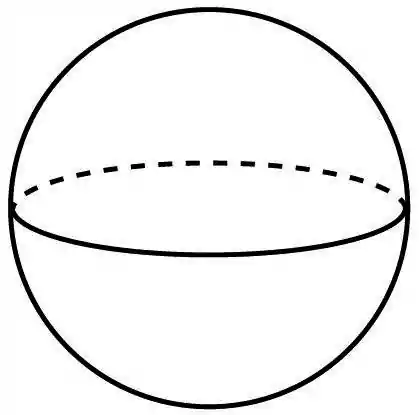
Já a esfera, sendo o seu raio, tem volume:
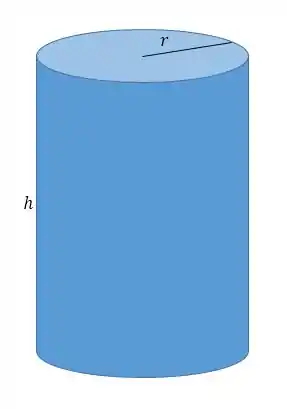
E o cilindro de raio e altura tem volume igual a:
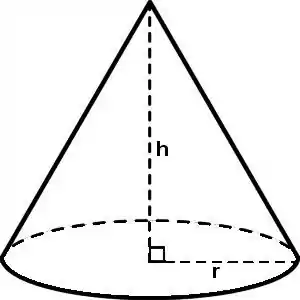
E o cone, que reserva uma vaga de estacionamento que não é sua, com raio e altura , tem volume igual:
Área lateral
A área lateral está associada ao volume é justamente a área da superfície que envolve o sólido, como destacado em azul já na primeira figura desse texto:
Para o paralelepípedo de lados , e , a área lateral é a soma das áreas de quadra retângulo que o compõe
Para a esfera de raio , a área lateral é:
O cilindro de raio e altura tem área da base igual a área da circunferência:
E área a superfície lateral igual ao comprimento da circunferência da base vezes a altura:
Por fim, o cone de raio e altura tem área lateral igual a:
Onde é geratriz:
Isso é tudo! Sabemos que não é pouco e gravar isso tudo é realmente complicado, por isso é importante fazer bastante exercícios para fixar. Vamos lá!
Principais fórmulas de área
Perímetro
Volume e principais fórmulas
Área lateral
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Uma folha de papel retangular com perímetro de foi dobrada no ponto A como na figura abaixo:
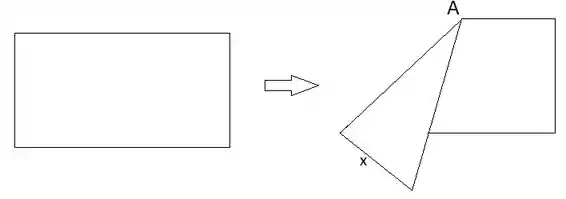
Determine a expressão da área da folha em função de .
Passo 1
A nossa folha é um retângulo. Para fazer a área do retângulo precisamos da sua base e sua altura. Olhando na figura, repara que a altura vai ser aquele que ele desenhou.
Falta achar a base. Para isso vamos usar o perímetro
Passo 2
Como ele disse que o perímetro é , vamos ter
Juntando tudo
Podemos simplificar geral por aqui
Passo 3
Agora que temos a base e a altura, vamos para a área
Abrindo essa conta, teremos
Resposta
Exercício Resolvido #2
Elaboração Própria
Ao redor de um jardim , vai ser construída uma calçada revestida de pedras. A largura dessa calçada é representada por e é medida em metros. Veja a figura.

- Qual a área ocupada pelo jardim?
- Escreva, na forma reduzida, um polinômio que expresse a área ocupada pela calçada?
- Se a largura da calçada for de e o preço do metro quadrado de revestimento de pedras for , quanto será o gasto?
Passo 1
a)
Reparaque o jardim tem um formato de retângulo. Ele tem de base e de altura.
A área vai ser
Passo 2
b)
O macete é notar que a área da calçada vai ser área do retângulo maior, que tem base e altura , menos a área do jardim.
Vamos começar achando a área do retângulo maior
Vamos fazer a distributiva nesse conta
A área da cálçada vai ser
Subsittuindo os valores
Passo 3
c)
E finalmente a última pergunta, basta que você use a equação encontrada e substitua os valores de medida que ele fornece que é .
Assim, vamos achar a área da cálçada, depois é só multiplicar pelo valor do
Vamos primeiro para a área
Chamando de o custo total, vamos ter
Resposta
Exercício Resolvido #3
Elaboração Própria
Considere um cubo cuja aresta vale e uma esfera interna ao cubo, e que tangencia as faces desse cubo.
Determine o volume interno do cubo que é externo à esfera.
Passo 1
Repara que o que ele quer é o volume interno do cubo e externo à esfera. Isso nada mais é que o volume do cubo, menos o volume da esfera. Vai ser a parte entre a esfera e o cubo.
Vamos chamar de esse volume, então:
Passo 2
Vamos começar achando o volume do cubo. Para isso, é só pegar a aresta do cubo e elevá-la a . Então
Passo 3
Agora precisamos do volume da esfera. Para isso, vamos usar a fórmula do volume da esfera.
Opa, mas precisamos do raio da esfera. E agora? Ele deu uma relação entre a esfera e o cubo. A esfera é interna ao cubo, e tangencia as duas faces. Vamos ver uma figura disso.
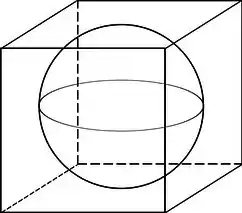
Repara que a altura do cubo, é igual ao diâmetro da esfera. Assim, vamos ter
E agora temos o raio em função daquele que ele deu no início.
Voltando para o volume da esfera, temos
Passo 4
Agora que achamos o volume do cubo e da esfera, podemos achar o volume que ele pediu.
Vamos ter
Aqui não temos muito o que fazer. Vamos deixar assim mesmo, e essa é nossa resposta
Resposta
Exercício Resolvido #4
Elaboração Própria
Se aumentarmos em o raio e a altura de um cone equilátero, em quantos por cento seu volume será aumentado?
Passo 1
Primeiro, vamos tentar entender o que ele quer. Repara que tínhamos um cone equilátero, aumentamos o seu raio e a altura, ele quer saber como vai ficar o volume.
Isso nos diz que temos que achar o volume do cone equilátero antes e depois desse aumento.
Lembrando que, o volume do cone é
Precisamos variar o raio e a altura aqui. Antes, vamos entender o que é um cone equilátero.
Quando olhamos um cone de frente, vemos um triângulo certo? Dá uma olhada nessa figura aqui
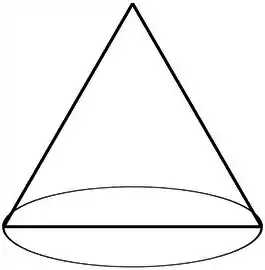
Esse é o nosso cone. O cone equilátero, é o cone que esse triângulo é um triângulo equilátero.
Assim, vamos ter
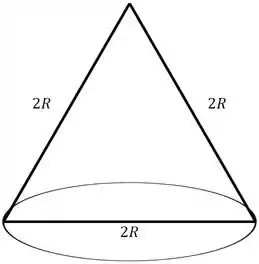
Passo 2
Beleza, agora precisamos achar o novo volume. Repara que vamos ter
E
Vamos passar essa porcentagem para decimal. Vamos ter
E
O novo volume vai ser
Trocando os valores do raio e da altura.
Passo 3
Agora temos que comparar o novo volume com o volume anterior. Repara que temos
Assim, vamos ter
Isso nos diz que
Repara que isso representa um aumento de no volume.
Resposta
aumento de no volume
Exercício Resolvido #5
Elaboração Própria
Considere uma folha de papel cujo perímetro é e um dos lados é o dobro do outro. A partir da união de duas arestas dessa folha se forma um cilindro. Determine o volume do cilindro com a maior área de base.
Passo 1
Temos uma folha de papel, vamos fazer o seu desenho

Não sabemos nem o a base nem a altura desse retângulo, mas ele disse que um dos lados é o dobro do outro. Assim, vamos ter
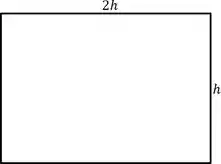
Além disso, conseguimos achar esse tranquilamente. Ele disse que o perímetro é .
Assim
Passo 2
Para fazer o cilindro, temos que “enrolar” essa folha. O detalhe é em qual direção vamos enrolar essa folha. Repara que vamos ter
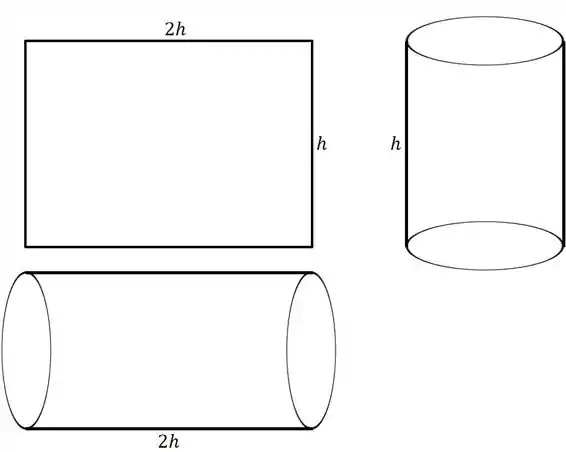
Eu desenhei ali as duas direções que eu posso rodar. Essa direção vai definir quem é a altura.
Ele quer o volume de um desses cilindros, mas qual?
Repara que ele falou o que tem maior área da base, então precisamos ver qual a área de cada uma dessas bases.
Passo 3
As duas bases são círculos. Para saber qual maior área, basta pegar a que tiver maior raio.
Então basta achar o raio da base de cada um desse cilindros.
Vamos começar com o seguinte cilindro
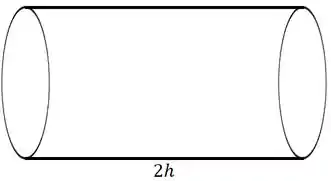
Repara que a altura se manteve como o comprimento da folha, enquanto o comprimento da base do cilindro vai ser igual à altura da folha.
Vamos chamar de o raio da base desse cilindro.
Assim, vamos ter
Trocando o valor de que achamos no passo
Passo 4
Vamos agora para o outro cilindro
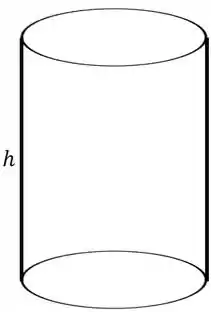
Repara que a altura se manteve como a altura da folha, enquanto o comprimento da base do cilindro vai ser igual ao comprimento da folha.
Vamos chamar de o raio da base desse cilindro.
Assim, vamos ter
Trocando o valor de que achamos no passo
Repara que esse raio, vai ser maior que o outro. Isso porque é maior que
Passo 5
Vamos ao volume desse segundo cilindro então.
Ele vai ser
Trocando o valor do raio e de , vamos ter
Resposta
Exercício Resolvido #6
Elaboração Própria
Dado o retângulo abaixo determine a sua área em função da sua diagonal sabendo que o perímetro do retângulo é

Passo 1
Aqui é mais uma daquelas questões que temos que achar a função de alguma coisa em relação a outra.
Dessa vez temos que achar a área desse retângulo em função da diagonal. Mas isso não é nada claro né? As vezes precisamos de várias equações e um algebrismo meio chato para chegarmos na função que ele pediu. Vamos começar pelo básico, achando a área do retângulo em função dos lados. Vamos chamar esses lados de e , assim vamos ter
Achamos a primeira relação, que deve ser a nossa função final, queremos , e ali temos a área em função de e . Então temos que continuar achando relações
Passo 2
A outra relação que temos que é o do perímetro do retângulo, que vai ser , assim
E
Po, achamos uma relação de novo só com e , e isso não ajuda em absolutamente nada né? Vamos deixar de lado essa por enquanto, pode ser que seja útil depois ou não, não tem como saber, vamos caçar mais uma.
Passo 3
Dessa vez vamos dar uma forçada na mente para achar uma relação que envolva , e .
Repara que temos um triângulo retângulo dentro da nossa figura lá no enunciado. Os catetos vão ser e e a hipotenusa vai ser , assim FINALMENTE temos uma relação entre eles , vamos aplicar Pitágoras
Passo 4
Agora temos vaaarias relações que podem ou não ser úteis, vamos escrevê-las todas aqui
Isso é tipo um sistema muito louco, aqui não tem jeito, precisamos de algumas marotagens para tentar resolver. A primeira coisa que você pode reparar é que temos uma soma de e na segunda equação, se elevarmos essa soma ao quadrado vai aparecer , e que envolvem as duas outras relações, então vamos começar fazendo esse cara ao quadrado esse cara ao quadrado
Podemos trocar a soma de com por por causa do Pitágoras, e o produto pela área pela fórmula da área. Vamos ter
E essa é a nossa função.