Transformada inversa de s^n
Produzido por Carolina SabaTeoria
Depois de ver tanta transformada, será que a gente já tem o que é preciso pra resolver:
Puts, perai, não temos ainda como achar esse cara! Pô, um tão simples, e ainda assim sem solução? Relaxa gafanhoto, aqui a gente vai ver como resolver ele. Pra começar, queremos achar tal que:
Belezita, por onde começar? Que tal modificar esse pra ele ganhar uma cara de algo que a gente conheça? Saca só:
Parece besteira, mas isso ajuda muito! Afinal, sabemos que:
Então na prática, o que temos é:
Opa opa, produto de transformadas? Isso tem cara de integral de convolução! Logo:
Caramba, já tamos chegando em algum lugar em! Daí em diante a gente pode puxar a definição da convolução mesmo, e saca só o que acontece:
Usado nosso querido e amado teorema fundamental do cálculo, podemos derivar os dois lados em relação a e achar:
E ta na mão galera! Achamos a a função cuja transformada da !
Transformada inversa de potências de s
Agora você provavelmente está pensando: se eu sei a transformada inversa de , será que sei a de , , etc.? Se você apostou que sim então é o seu dia de sorte! Vamos manter a mesma ideia, só que dessa vez tentar achar tal que:
Oras, se ainda tivermos em mãos a ideia da convolução:
E galera, dai em diante não muda muita coisa! Repetimos a definição da convolução e o teorema fundamental do cálculo:
E logo:
Bem, deu pra ver que se quiséssemos achar pra os procedimentos seriam os mesmos. Podemos generalizar então para:
Transformada inversa de potências de s
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Calcule
Passo 1
Fala galera, bora começar? Antes de mais nada, vamos lembrar de uma propriedade bacana:
Pois bem, isso parece um pouco com nossa questão, né não? Vamos comparar:
Show, isso significa que:
Ou seja:
Fechando com chave de ouro:
E logo:
Resposta
Exercício Resolvido #2
Elaboração própria.
Prove que:
Passo 1
Essa propriedade do Delta de Dirac é bem tranquila de provar se a gente lembrar da seguinte propriedade também:
Como isso ajuda a gente? Bem, da uma olhada na propriedade:
Tem um solto com expoente e, ao mesmo tempo, temos um sinal de menos. Bem, isso aí é um bom sinal de que podemos usar pr obter:
Passo 2
Bem, agora que temos uma relação que aparece um termo de com expoente , que tal tentarmos fazer resultar em algo cuja transformada inversa conhecemos. Bem, seja
Vamos ter:
Show de bola, achamos . Mas eaí? Pra gente terminar meeesmo, precisamos lembrar que lá no início desse passo definimos:
Logo:
Po, se tem duas definições diferentes e as duas tão certas, basta igualar elas! E ai sim achamos a relação do enunciado:
Resposta
- Ao definirmos , temos que
- Ao definirmos , temos que se usarmos a propriedade das transformadas
- Ao igualarmos as duas definições de encontradas, obtemos a propriedade do enunciado
Exercício Resolvido #3
Elaboração própria.
Calcule
Passo 1
Beleza, olha só. Pra questões desse tipo, com polinômios sobre polinômios, as chances de dar pra simplificar são enormes. Sendo assim, vamos olhar pro denominador que é mais simples. Veja que se , então o denominador assume o valor . O que será que acontece com o numerador usando o mesmo ?
Opa, então é uma raiz do polinômio no numerador.
Passo 2
Você pode estar se perguntando: como isso ajuda a gente? Bem, veja só, se sabemos uma raiz do polinômio, podemos dividir ele usando Briot Ruffini (BR). Montando a matriz BR temos:

Descemos o número e multiplicamos ele pela raiz conhecida, somando ao próximo número. O resultado dessa conta, a gente põe logo a baixo:

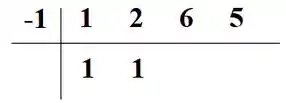
Repetimos o processo pro recém escrito, somando dessa vez com o próximo número na parte de cima, isto é, o número :
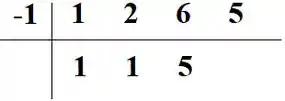
E pra fechar, fazemos uma última vez seguindo a mesma ideia
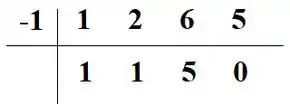
Sendo o último número o resto , a raiz conhecida do polinômio do numerador, a matriz BR nos revela que podemos reescrever o polinômio para:
Passo 3
Na verdade pessoal, a gente feshow essa questão já! Veja só, usando a simplificação que calculamos no passo anterior: