Delta de Dirac e Função Degrau
Produzido por Carolina SabaTeoria
Hoje a gente vai aprender a relação entre o delta de Dirac e a Função degrau! Mas antes de qualquer coisa…O que é delta de Dirac? O que é função degrau? ? 😖
O detlta de Dirac é uma função impulso, ou seja, ela assume valores muito altos em um intervalo de tempo muito curto
Já a função degrau, também chamada de função de Heaviside é literalmente uma função em forma de degrau! 🤣🤣🤣
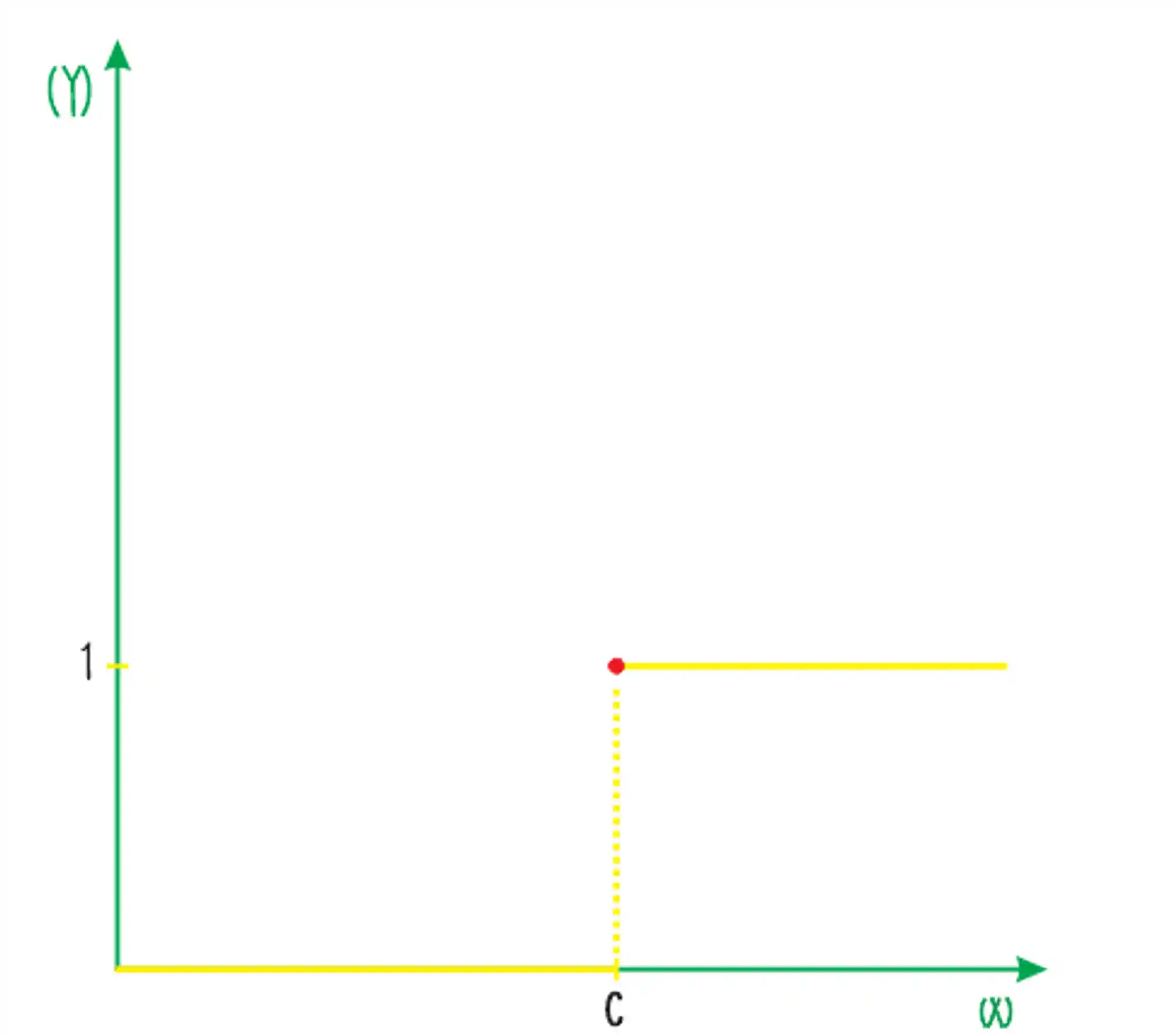
Ela é suuper importante quando precisamos calcular a transformada de funções que possuem degraus. A gente tem um conteúdo interinho só sobre esse tipo de função, você pode conferir clicando aqui!
📢 Clique para saber mais:
- Delta de Dirac e Função Degrau: Exercícios Resolvidos
- Tabela Transformada de Laplace
- Transformada de Laplace da Função Degrau
Delta de Dirac como uma Força
Vamos considerar uma força com tamanho
Onde:
O gráfico fica com essa carinha aqui:
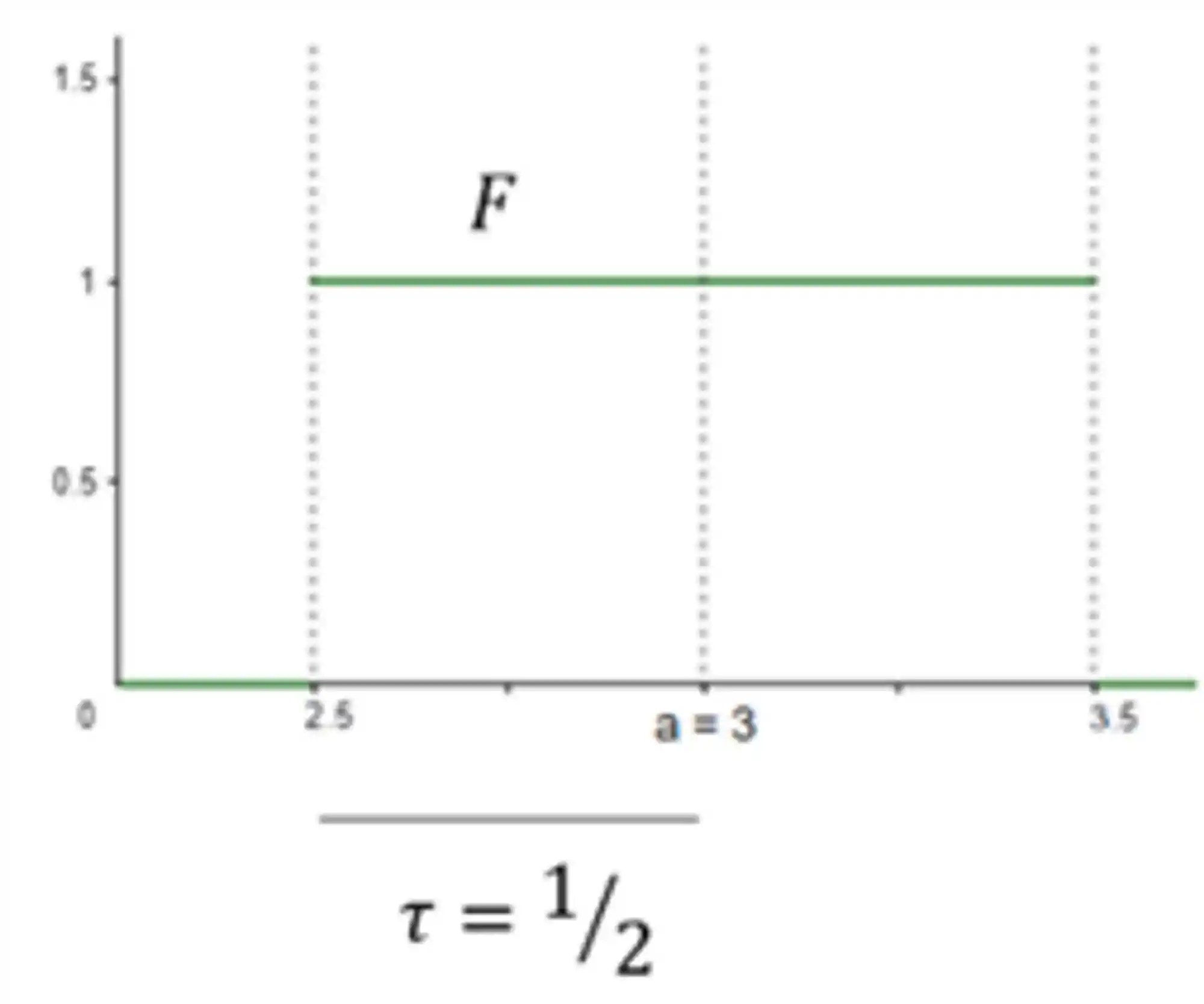
Para mostrar por quanto tempo ela dura, demos um valor qualquer pra τ. Mas quem é essa força, você talvez esteja me perguntando. Alguns fenômenos físicos com forças como essa são:
- Força eletromotriz que um circuito elétrico recebe;
- Força aplicada a um sistema massa-mola
- Qualquer objeto inicialmente em repouso, posto em movimento por causa de uma força.
Imagine agora que essa força seja instantânea. Pra isso, fazemos:
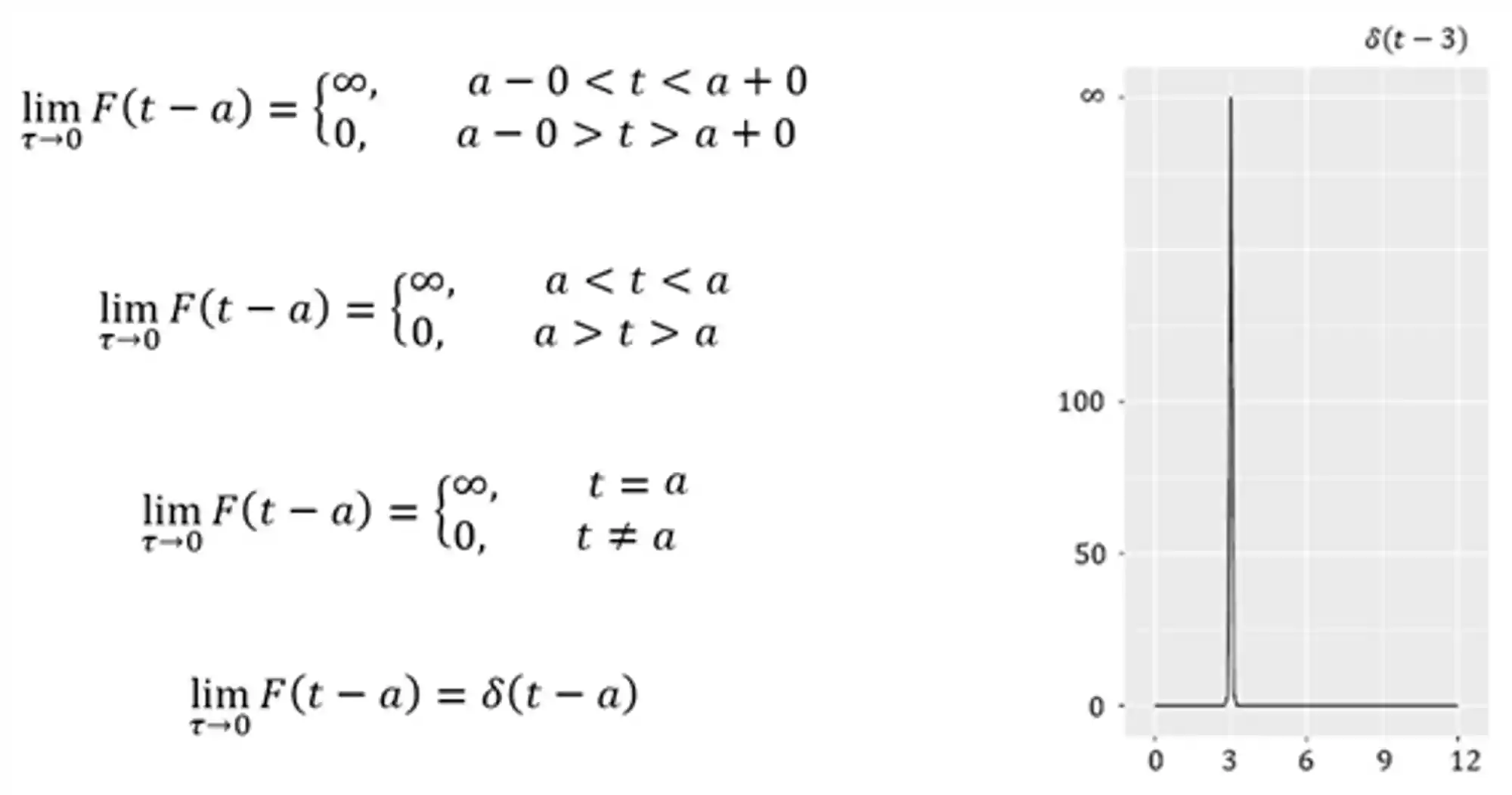
Ou seja,
Mas como a função só tá definida para $ a-τ
Ou seja, se entendermos o Delta de Dirac como uma força, revelamos uma propriedade interessantíssima dele:
E isso ainda vale se a lei de formação da força for diferente da que usamos. Afinal, o Delta de Dirac pode ser definido pelo limite de funções com propriedades análogas a sequência de pulsos como essas:
Mas o que isso tem a ver com a Função Degrau? Vamos ver agora!
Relação entre Função Degrau de Delta de Dirac
Vamos imaginar que queremos achar o valor de:
É bem parecido com a propriedade que achamos acima, né não? Com a diferença que o t agora é variável. Pois bem, já que a definição do Delta de Dirac é:
Vamos poder imaginar duas possibilidades para o valor do limite superior de integração

Onde a primeira integral é a propriedade do Delta de Dirac que achamos anteriormente:
E chegamos na função degrau! Pra fechar com chave de ouro e achar a relação entre ela e o Delta de Dirac basta pedir ajuda pro nosso querido amigo Teorema Fundamental do Cálculo e derivar dos dois lados em relação a t:
Agora vamos praticar com exercícios?
Relação entre Função Degrau de Delta de Dirac
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Prove que, para , temos como verdade:
Passo 1
Bora lá então. Olha só, mesmo tendo um Delta de Dirac dentro dessa integral, podemos resolver esse carinha usando propriedades de integrais. Afinal, temos um produto de funções de tipos diferentes, o que geralmente nos pede pra fazer integração por partes. Seja então:
Nossa integral pode ser entendida como:
E pela integração por partes, vamos ter:
E dai em diante podemos separar em dois pedações e resolver cada um.
Passo 2
Vamos começar com . Lembrando da definição:
Como , vamos ter que:
E logo:
O resultado desse pedaço da integração por partes será:
Passo 3
Agora vamos calcular aquela integral que ficou faltando. Bem, já que ela é:
Podemos transformar ela em duas na verdade, já que , ficando então com:
Mas como:
No final das contas a gente fica com:
Opa, e olha só, temos a integral de uma derivada! Não importa quem for , esse resultado será:
Passo 4
Agora a gente junta tudo. Já que:
Temos então:
Provadíssimo!
Resposta
Por integração por partes:
Conseguimos provar que:
Exercício Resolvido #2
Elaboração própria.
Prove que, para , temos como verdade:
Passo 1
Vamos começar. Apesar de termos Delta de Dirac dentro dessa integral, podemos resolver usando propriedades de integrais. Afinal, como temos um produto de funções de tipos diferentes, uma boa ideia é usar integração por partes. Seja então:
Nossa integral pode ser entendida como:
E pela integração por partes, vamos ter:
A integral que ficou sobrando não vai sair daí facilmente, então vamos dedicar um passo na resolução só pra ela, beleza?
Passo 2
Show, pra resolver:
A gente pode lembrar que ela também é uma integral com produto de funções diferentes. Portanto, seja:
Nossa integral pode ser entendida como:
E pela integração por partes, vamos ter:
E juntando isso no resultado do passo , temos:
E pronto, agora podemos ver cada um dos pedaços isoladamente
Passo 3
Então, o primeiro pedaço vai ser:
O que vai dar:
Mas pela definição do Delta de Dirac:
Acabamos concluindo que esse pedaço todo é igual a :
Passo 4
Vamos pro segundo pedaço então, com . Lembrando da definição:
Como , vamos ter que:
E logo:
O resultado desse pedaço da integração por partes será:
Passo 5
Agora vamos calcular aquela integral que ficou faltando. Bem, já que ela é:
Podemos transformar ela em duas na verdade, já que , ficando então com:
Mas como:
No final das contas a gente fica com:
Opa, e olha só, temos a integral de uma derivada! Não importa quem for , esse resultado será:
Passo 6
Agora a gente junta tudo. Já que:
Temos então:
Provadíssimo!
Resposta
Por integração por partes sendo feita duas vezes, uma primeira usando:
E uma segunda usando:
Conseguimos provar que: