Discordância em hélice
Produzido por Erick PinhoTeoria
E aí galera!!! Tudo bem com vocês?
No texto anterior vimos que discordâncias em linha são defeitos cristalinos que causam a distorção da rede cristalina em torno de uma linha. Além disso, vimos que as discordâncias são imperfeições importantes por tornar o material metálico muito mais dúctil devido à sua presença.
Agora vamos conhecer outro tipo de discordância em linha que também é muito importante, a discordância em hélice.
Mas afinal, o quê é uma discordância em hélice?

Para entendermos o quê é uma discordância em hélice vamos fazer o seguinte exercício: primeiramente vamos imaginar uma rede cristalina perfeita, depois cortamos parte dessa rede, igual à figura abaixo, e torcemos o sólido deslocando em uma distância atômica, e então o sólido formado é um sólido com uma discordância em hélice, conforme figura abaixo.
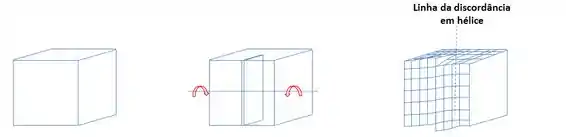
Imaginem agora, que estamos dando uma volta em torno da linha de discordância em hélice saindo do ponto x, no sentido horário, e indo até y. Quando chegamos ao ponto y, ao terminarmos a volta, notamos que estamos afastados do ponto x uma posição atômica abaixo. Assim, um vetor é necessário para completar a voltar e retornarmos à origem (ponto x) e esse vetor é conhecido como vetor de Burgers b. Caso continuássemos a percorrer ao redor desse defeito, iríamos traçar um caminho em espiral ou hélice.
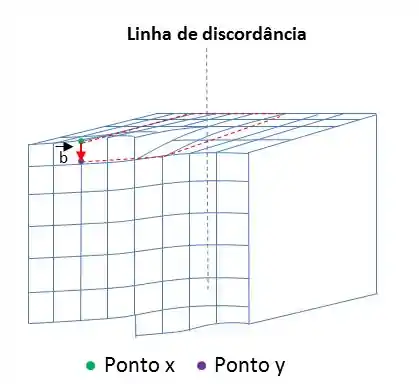
Note que o vetor de Burgers b é paralelo à linha de discordância.
Escorregamento
Para que ocorra a movimentação das discordâncias é necessário impormos uma componente de tensão cisalhante. Tanto para a discordância em aresta quanto para a discordância em hélice essa componente de tensão cisalhante deve agir paralelamente ao vetor de Burgers. Se essa tensão cisalhante for suficientemente grande a discordância se move, a esse movimento dá-se o nome de escorregamento.
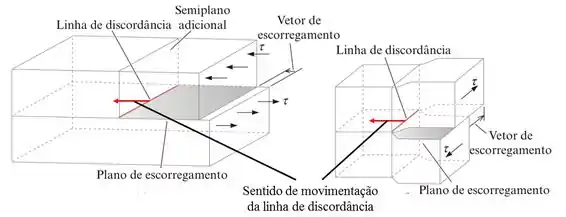
Como podemos notar o sentido de movimentação da linha de discordância em aresta segue um plano de escorregamento que é formado pela linha de discordância e o vetor de Burgers, que são perpendiculares entre si. Neste escorregamento o semiplano adicional é “empurrado” pela tensão de cisalhamento, logo o sentido de movimentação da discordância é o mesmo sentido da tensão de cisalhamento, ou seja, perpendicular ao vetor de Burgers.
Para a movimentação da discordância em hélice não é possível definirmos o plano de escorregamento como sendo a linha de discordância e o vetor de Burgers, uma vez que eles são paralelos.
Logo, durante o escorregamento a discordância move-se de uma região para outra no cristal. A tensão de Peierls-Nabarro é a tensão de cisalhamento necessária para mover de um local de equilíbrio para outro:
Onde e são constantes do material, é modulo do vetor de Burgers e é a distância entre planos de escorregamento adjacentes. A discordância se move em um sistema de escorregamento que requeira o menor gasto de energia.

Da equação de Peierls-Nabarro é possível identificarmos os vários fatores que determinam os sistemas de escorregamento que estarão ativos:
- A tensão necessária para mover uma discordância aumenta exponencialmente com o módulo do vetor de Burgers. Assim, quanto menor for o módulo de vetor de Burgers menor será a tensão, ou elevada densidade linear, menor a tensão necessária para mover a discordância.
- A tensão necessária para mover uma discordância diminui exponencialmente com o aumento da distância entre os planos de escorregamento. Logo, quanto maior for a distância entre os planos de átomos menor será a tensão necessária para mover a discordância.
Vamos fazer um exemplo sobre o cálculo do vetor de Burgers?!
Exemplo: Calcule o módulo do vetor de Burgers no cobre.
Solução: A primeira coisa que devemos saber é qual é a estrutura cristalina do cobre. O possui estrutura cristalina CFC, logo o parâmetro de rede () é de . A direção de escorregamento ou direção do vetor de Burgers é da família . Assim, a distância de repetição ao longo das direções corresponde à metade da diagonal da face, já que os pontos de rede estão localizados nos vértices e centros das faces.
Assim, o módulo do vetor de Burgers (ou a distância de repetição) é:
Importância das discordâncias
A deformação plástica é uma deformação permanente, ou seja, é uma mudança irreversível de forma mesmo após a remoção da tensão que causou a deformação. A tensão aplicada provoca o movimento da discordância, e o efeito cumulativo do escorregamento de diversas discordâncias é a deformação plástica. Por isso, as discordâncias são muito importantes em metais e ligas, pois é através delas que os metais e ligas sofrem a deformação plástica. É preciso diferenciar uma deformação plástica de uma deformação elástica. A deformação elástica é uma mudança temporária da forma, isto é, depois de cessado a tensão que a causou o material retorna ao seu estado inicial. Essa mudança na forma é resultado do estiramento das ligações atômicas, mas sem causar o movimento de discordâncias.

A figura acima é um exemplo de deformação elástica causada por uma determinada força, que depois de cessada a força o estado final do material é igual ao seu estado inicial.
O processo de escorregamento das discordâncias é importante para a compreensão do comportamento mecânico dos metais. Primeiramente o movimento das discordâncias explica por que a resistência dos metais é muito inferior à resistência de suas ligações atômicas. Caso ocorra um escorregamento, apenas uma pequena fração das ligações metálicas precisa ser rompida, e a tensão necessária para deformar o metal é bastante reduzida.
Em segundo lugar, o escorregamento realizado pela movimentação de discordâncias proporciona ductilidade aos metais. Caso não houvesse as discordâncias, por exemplo, os metais não poderiam ser conformados como produtos úteis, conforme figura abaixo.
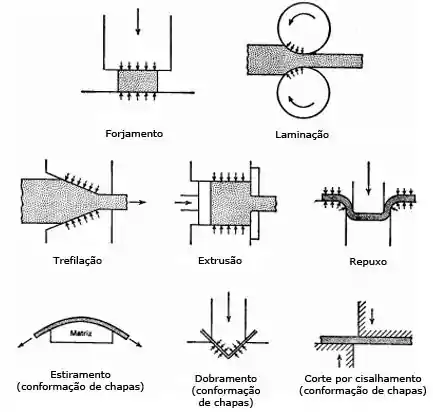
Em terceiro lugar, podemos controlar as propriedades mecânicas de um metal ou liga interferindo no movimento das discordâncias, para aumentar a dureza ou a ductilidade. Por exemplo, podemos inserir no metal obstáculos que dificultam o movimento das discordâncias, a menos que sejam aplicadas tensões mais elevadas, não conseguiremos deforma-los. Assim, a presença de discordâncias contribui para tornar os materiais metálicos mais resistentes mecanicamente.
A densidade de discordâncias é uma medida da quantidade de discordâncias presentes em determinado volume de material. Essa medida é importante, pois há uma quantidade muito grande de discordâncias presentes nos materiais. Densidades de discordâncias de são típicas de metais dúcteis. Porém, é possível obter densidades de até ao se deformar intensamente um material.
Escorregamento
Importância das discordâncias
Exercícios Resolvidos
Exercício Resolvido #1
Lista de exercício UFSC
Quais são os dois tipos fundamentais de discordâncias? Caracterize-as e desenhe esquematicamente cada uma delas.
Passo 1
Os dois principais tipos de discordâncias são: em cunha (aresta) e em hélice (espiral). Discordâncias em aresta são o resultado da adição de um semiplano na rede cristalina. Esse semiplano distorce a rede em sua volta, produzindo duas regiões: uma sobre compressão, do lado do semiplano, e uma sobre tração, do lado oposto. Neste tipo de discordância o vetor de Burgers é perpendicular a linha de discordância e o plano de escorregamento é formado pela linha de discordância e o vetor de Burgers. Já as discordâncias em espiral são resultadode uma torção da rede. Essa torção produz, também, regiões de compressão e de tração em torno de uma linha. O vetor de Burgers dessas discordâncias são paralelos à linha de discordância. Neste tipo de discordância não é possível definir o plano de escorregamento como na discordância em aresta.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Callister W.D. Ciência e Engenharia de Materiais. Sétima edição. Cap.4.
É possível que duas discordâncias esperiais com sinais opostos se aniquilem mutuamente? Explique sua resposta.
Passo 1
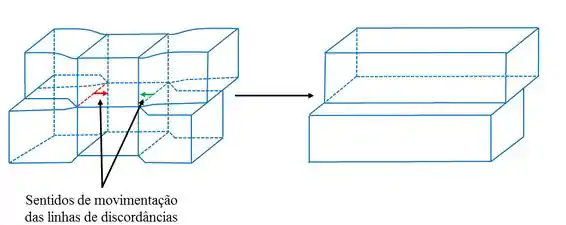
Comforme podemos notar na figura abaixo, se duas discordâncias em espiral estiverem no mesmo plano elas irão aniquilarem-se quando as duas linhas das discordâncias se encontrarem.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Lista de exercício UFSC
Como a direção de movimento de uma linha de discordância em espiral e em cunha relaciona-se com a direção da tensão de cisalhamento aplicada? Faça um esquema.
Passo 1
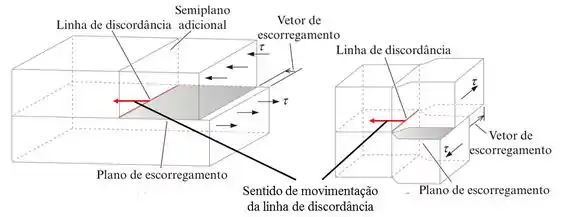
Através do esquema abaixo, nota-se que a tensão de cisalhamento move a discordância em aresta na mesma direção de aplicação da tensão. Já para o discordância em espiral a direção de movimentação da linha de discordância é perpendicular a direção de aplicação da tensão de cisalhamento.

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Lista de exercício UFSC
O que é escorregamento?
Passo 1
É o processo pelo qual as discordâncias movimentam produzindo deformação plástica no material. Essa deformação plástica é simplesmente uma deformação permanente no material causada pela movimentação ou escorregamento da discordância, em resposta a uma tensão cisalhante aplicada ao material.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Lista de exercício UFSC
Defina um sistema de escorregamento. Todos os metais possuem o mesmo sistema de escorregamento? Explique.
Passo 1
A movimentação da discordância se dá através de planos e direções preferenciais, ou seja, o movimento da discordância ocorrerá com maior facilidade em planos com elevada densidade planar e direção de escorregamento com elevada densidade linear. Para esses planos e direções de escorregamento dá-se o nome de sistema de escorregamento. O escorregamento ocorre mais facilmente entre planos de átomos mais afastados entre si, isto é, com uma distância entre os planos relativamente grande e a direção de escorregamento com elevada densidade linear, ou seja, pequena distância de repetição das células unitárias. Logo, o escorregamento ocorrerá em um sistema que requeira o menor gasto de energia. Assim, os metais não possuem o mesmo sistema de escorregamento, uma vez que eles têm estruturas cristalinas diferentes. Por exemplo, metais com estrutura cristalina CFC possuem 12 sistemas de escorregamento, ao passo que os com estrutura HC possuem 3 sistemas, por isso que metais com estrutura CFC são mais dúcteis do que os com estrutura HC.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Lista de exercício UFSC
Qual é o efeito nas propriedades mecânicas de um material metálico quando se dificulta o movimento das discordâncias?
Passo 1
O movimento das discordâncias está relacionado com a capacidade que o metal tem de se deformar plasticamente, isto é, quanto mais fácil for a movimentação das discordâncias no metal maior será,também, sua ductilidade. Assim, quando se dificulta o movimento das discordâncias torna-se o material mais resistente mecanicamente, ou seja, promove-se uma maior rigidez do material, uma vez que há impedimento (dificuldade) da movimentação das discordâncias. Desse modo aumentamos a resistência a tração e o escoamento e diminuímos a tenacidade e a ductilidade do material.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Lista de exercício UFSC
Explique brevemente porque metais HC são mais frágeis do que metais CFC ou CCC? Obs: Utilize os conhecimentos sobre discordâncias.
Passo 1
Metais com estrutura HC possuem 3 sistemas de escorregamento e metais com as estruturas CFC ou CCC possuem 12 sistemas de escorregamento. Quanto mais sistemas de escorregamento maior é a probabilidade (possibilidade) das discordâncias movimentarem-se e, consequentemente, mais dúcteis serão. Assim, metais HC possuem menos números de sistemas de escorregamento, o que torna-os mais frágeis (menor ductilidade) do que os metais CFC e CCC, que possuem um número mais de sistemas de escorregamento, o que os tornam mais dúcteis.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
Elaboração própria
Por que as soluções sólidas em ligas metálicas fazem que estejam mais duras e resistentes que o metal base?
Passo 1
Em soluções sólidas, os átomos de soluto ocupam os interstícios ou substituem os átomos do metal base, com isso os átomos de soluto tornam-se barreiras à movimentação das discordâncias. Dificultando a movimentação das discordâncias torna-se o metal em soluções sólidas mais duros e resistentes, ou seja, a restrição ao movimento das discordâncias confere maior dureza e resistência ao material. Por exemplo, ao adicionarmos estanho em um matriz de cobre puro produzimos uma solução sólida com maior dureza do que a do cobre puro.
Resposta
Ei, a resposta está no passo a passo :)