Faça um esboço do cilindro de equação dada.
Passo 1
a)Tudo que precisamos saber para esboçar o gráfico de um cilindro é saber qual a curva diretriz do cilindro e qual o eixo do cilindro.
Passo 2
A primeira coisa é entender que curva diretriz é essa.
Isso lembra muito uma circunferência, até porque ele é uma circunferência!
A forma geral da circunferência é
Não precisa ser e , pode qualquer dois entre , e . Lembrando que é o centro da circunferência e é o raio da circunferência. Esse zero é porque a circunferência “está” no plano com , que é a outra variável.
Podemos ver então que o centro vai ser
E o raio vai ser
Portanto, nossa curva diretriz é , que é uma cincunferência de raio e centro . Logo, o eixo do cilindro será o eixo que contém a variável livre, nesse caso o eixo .
Passo 3
Agora que já sabemos qual a curva diretriz e qual o eixo do cilindro, podemos começar seu esboço.
Vamos plotar a curva diretriz no plano .
O gráfico vai ficar:

Passo 4
Como fazemos o cilindro agora? Repita a curva diretriz um pouco mais acima, representando os valores positivos e um pouco mais abaixo, representando so valores negativos. Fica assim:
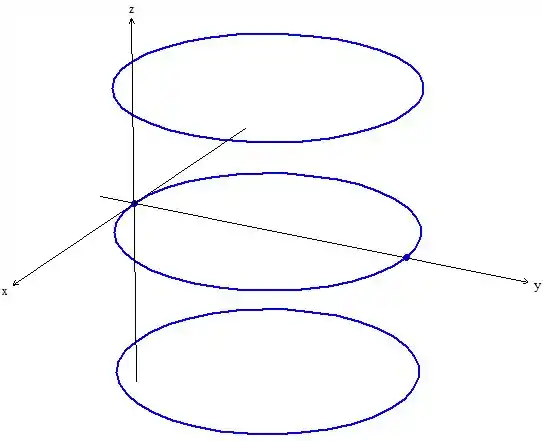
Passo 5
Vamos colocar retas paralelas(geratrizes) ao outro eixo (eixo do cilindro). Veja essa figura de como fica:
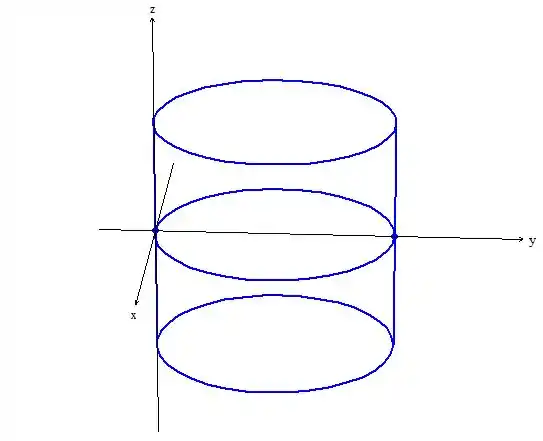
Passo 6
Agora é só hachurar a superfície delimitada pelas figuras. Fica assim:
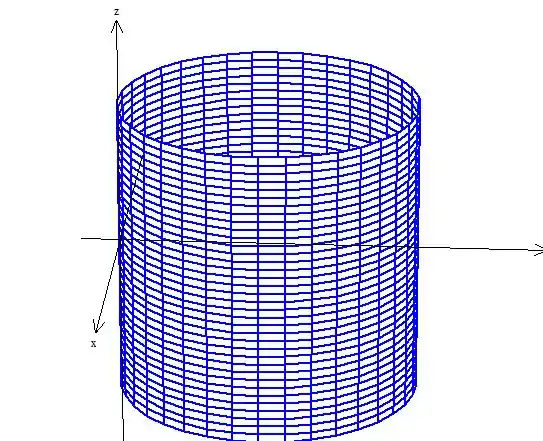
Passo 7
b)
A primeira coisa é entender que curva é essa.
De novo temos uma circunferência, dessa vez o plano que vamos pegar como base que é diferente. Vai ser o plano .
O centro vai ser
O raio vai ser
Portanto, nossa curva diretriz , que é uma cincunferência de raio e centro . Logo, o eixo do cilindro será o eixo que contém a variável livre, nesse caso o eixo .
Passo 8
Agora que já sabemos qual a curva diretriz e qual o eixo do cilindro, podemos começar seu esboço.
Vamos plotar a curva diretriz no plano .
O gráfico vai ficar:
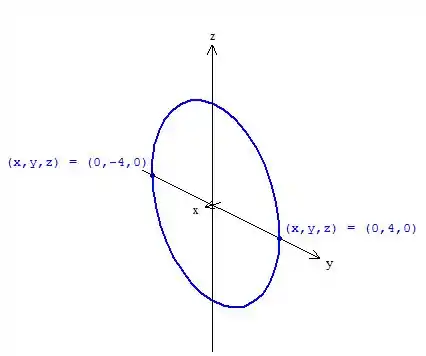
Passo 9
Agora, vamos repetir a figura, uma mais para trás, representando a parte negativa e uma outra mais para frente, representando a parte positiva. Fica assim:
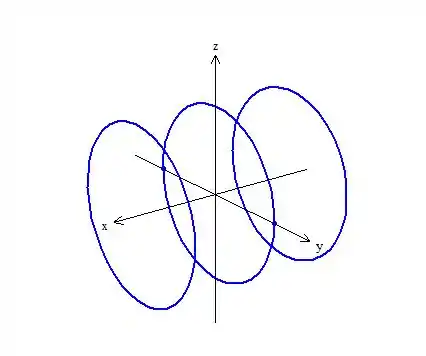
Passo 10
Como fazemos o cilindro agora? Simples, vamos colocar retas paralelas(geratriz) ao outro eixo(eixo do cilindro). Olha essa figura de como fica:
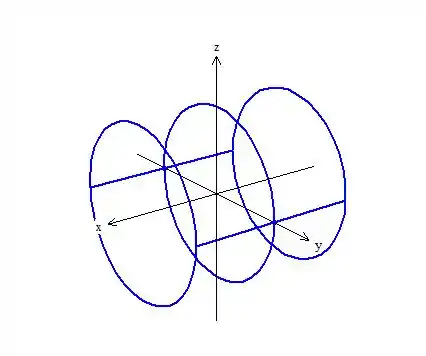
Passo 11
Hachurando a área delimitada pela figura temos:
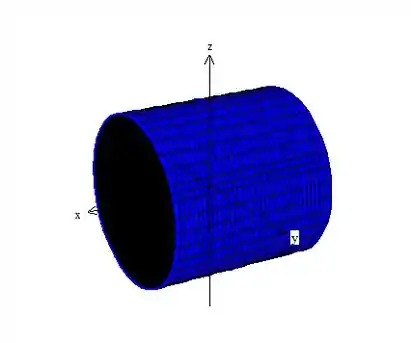
Resposta
Ei, a resposta está no passo a passo :)