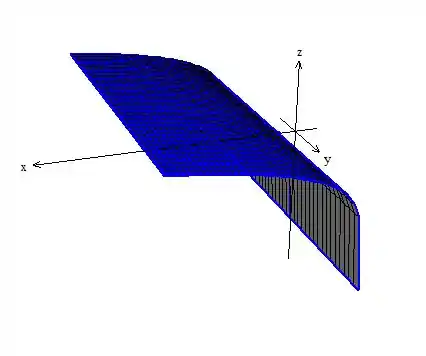
Faça um esboço do cilindro de equação dada.
Passo 1
A variável irrestrita é e consequentemente o eixo do cilindro é o eixo .
A curva diretriz é
Logo já identificamos os principais elementos para esboçar o gráfico do cilindro.
Passo 2
Vamos esboçar a curva diretriz no plano . A curva diretriz é . Portanto temos:
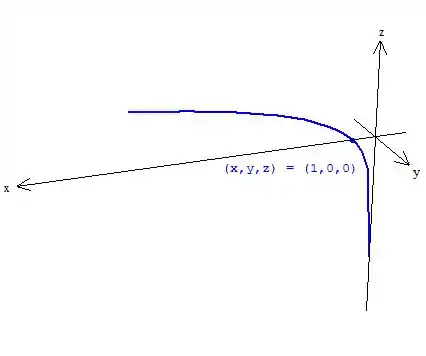
Passo 3
Depois disso, vamos repetir a curva diretriz, um pouco mais a frente, representando os valores positivos e um pouco mais atrás, representandoos valores negativos. Fica assim:
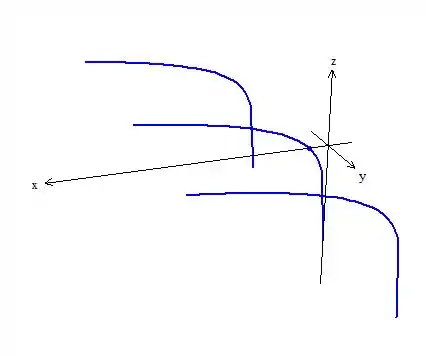
Passo 4
Agora, vamos colocar retas paralelas(geratrizes) ao outro eixo(eixo do cilindro)
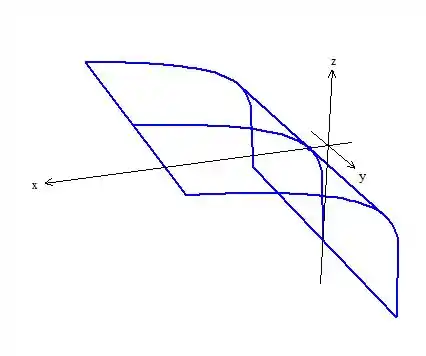
Passo 5
Hachurando a superfície, eis aí o nosso cilindro!
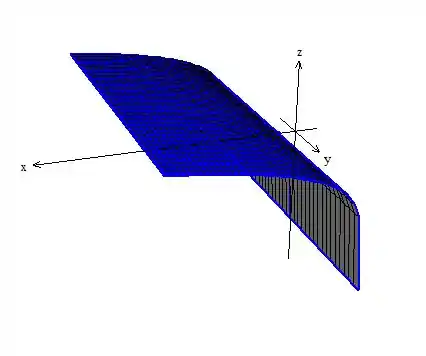
Resposta