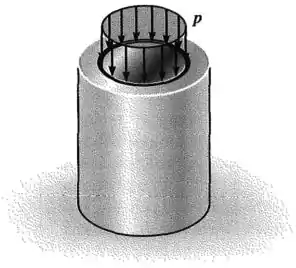
O tampão tem diâmetro de e ajusta-se ao interior de uma luva rígida com diâmetro interno de . Ambos, tampão e luva, têm de comprimento.
Determine a pressão axial que deve ser aplicada à parte superior do tampão para que ele entre em contato com as laterais da luva. Determine também a que distância o tampão deve ser comprimido para baixo para que isso aconteça.
O material do tampão tem e .
Passo 1
O que está acontecendo?
O tampão tem um diâmetro inicial e um comprimento inicial .
O seu material tem um módulo de elasticidade e um Coeficiente de Poisson .
E ele está submetido a uma pressão axial de compressão.
Agora vamos pensar...
Pressão é força sobre área, então essa pressão pode ser trocada por uma força equivalente , onde é a área da seção transversal do tampão.
Essa força de compressão vai gerar no tampão uma força interna normal e uma tensão normal média:
Substituindo , temos:
Ou seja, para o equilíbrio interno do tampão, a tensão tem que ser o oposto da pressão .
E o que é que o exercício quer?
Ele quer saber qual é a pressão que faz com que o tampão encoste nas laterais da luva.
Ou seja, ele quer saber qual é a pressão que faz com que o diâmetro final do tampão seja igual ao diâmetro interno de na luva.
Agora, Para que o tampão tenha esse diâmetro final , ele tem que ter sofrido:
- Uma certa deformação lateral ;
- Uma certa deformação longitudinal , de acordo com seu coeficiente de Poisson ;
- E uma certa tensão normal média , de acordo com a Lei de Hooke .
Então combinando a Lei de Hooke, as definições do coeficiente de Poisson e da deformação lateral e a relação , vamos poder relacionar a pressão com o diâmetro final e encontrar o valor de que garante que .
Depois, o exercício ainda quer que a gente encontre a variação de comprimento que o tampão sofreu.
Para tanto, vamos ter que usar a definição , a Lei de Hooke (para encontrar a deformação correspondente a uma certa tensão normal ) e a relação .
Passo 2
Queremos relacionar então a pressão axial no tampão com o seu diâmetro final .
Para tanto, vamos começar usando a Lei de Hooke:
Aplicando a relação , temos:
Agora, vamos pensar...
Precisamos relacionar não com a deformação longitudinal , mas sim com a deformação lateral no tampão, já que é a deformação lateral que causa a variação no diâmetro do tampão.
Para encontrar em função de , usamos a definição do Coeficiente de Poisson :
Isolando , temos:
Substituindo essa expressão na equação que tínhamos encontrado anteriormente, temos:
Agora, só falta descrever essa deformação lateral em função do diâmetro final que vamos obter uma expressão para a pressão em função de .
A deformação lateral é definida como a variação de uma medida no sentido lateral (como o diâmetro, por exemplo) sobre o valor original da medida, ou seja:
Substituindo isso na última expressão que tínhamos encontrado para , temos que:
Passo 3
Agora que já encontramos uma expressão que relaciona a pressão axial no tampão com o seu diâmetro final :
podemos substituir os valores , , e nessa expressão para descobrir qual é a pressão axial que faz com que o tampão encoste nas laterais da luva:
Calculando tudo, isso dá:
Esse é um número pequeno, então fica melhor reescrevê-lo em :
Passo 4
Já resolvemos a primeira parte do exercício, que foi encontrar a pressão que faz com que o tampão tenha um diâmetro final .
Agora, queremos resolver a segunda parte: descobrir a distância que o tampão teve que ser comprimido para baixo para que isso aconteça.
Essa distância é a variação de comprimento do tampão, que é descrita pela sua deformação longitudinal :
Onde e é o seu comprimento original de do tampão.
Isolando nessa definição de , temos:
A gente não conhece o valor de , mas a gente sabe que essa deformação é proporcional à tensão normal média no tampão de acordo com a Lei de Hooke:
Mas como vimos no primeiro passo, , então:
Substituindo isso na expressão que tínhamos encontrado para a variação de comprimento , ela fica assim:
Então substituindo nessa equação , vamos descobrir qual é a variação de comprimento que corresponde a essa situação.
Fazendo essa substituição e ainda substituindo os valores de e , temos:
Para que o resultado saia em milímetros (), reescrevemos o módulo de elasticidade de como :
Calculando, encontramos:
Ou seja, o tampão teve que ser comprimido para baixo para que ele encostasse nas laterais da luva.