Sejam e , respectivamente, os trechos das parábolas e , com ponto inicial (-1,0) e final (1,0). Seja um campo de vetores de classe em tal que , para todo .
Se então a integral é igual a:
Passo 1
Bom, pra começar vamos ver as curvas que estamos trabalhando.
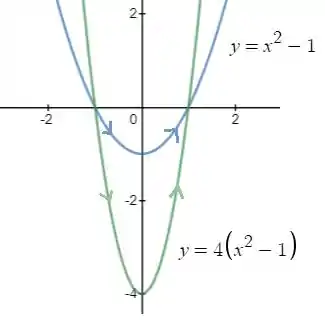
Pelo teorema de green, temos que
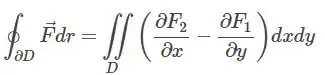
Onde nesse caso, o vai ser
Precisamos ainda de manter a orientação positiva. Observa que esse não é o caso. Para mantermos tudo rodando no sentido anti-horario, precisamos mudar o sentido de giro da curva azul, no caso a .
Então nosso teorema ficará:
Passo 2
Ele nos passou o valor de
Então ficamos com:
Passo 3
Calculando então nossa integral dupla:
Do enunciado temos que essa diferença vale ;
Descrevendo a região vemos que
E também percebe-se que y varia entre a função verde debaixo e a azul de cima.
Passo 4
Escrevendo e resolvendo a integral dupla ficamos com:
Passo 5
Voltando ao teorema ficamos com: