Uma partícula de massa e energia constante move-se sobre o eixo na presença de um degrau de potencial.
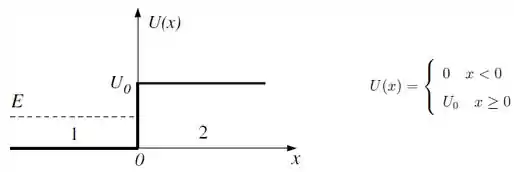
- Escreva as soluções gerais e da equação de Schrödinger nas regiões () e ().
- Escreva as condições de contorno que e devem satisfazer.
- Determine e a menos de uma única constante multiplicativa.
Passo 1
Letra a)
A equação de Schrödinger é dada por:
Na região , , e temos:
Chamando , temos:
A função que derivada duas vezes resulta nela própria multiplicada por um sinal negativo é o seno e o coseno. Logo:
Na região , , e temos:
Onde . Assim, definindo , temos:
Neste caso, como não temos um sinal negativo, ficamos com:
Contudo, como essa função é para , vamos ter que cortar a parte , porque ela tende ao infinito quando . Isso faria com que não pudéssemos usar a condição de normalização na função de onda (ela não seria normalizável!).
Uma última observação: Nota que ele dá o valor da energia total.
Assim, temos:
Logo:
E as soluções gerais ficam:
Passo 2
Letra b)
A função de onda deve ser contínua e suave em todo o espaço.
Ela ser contínua significa dizer que em , onde o potencial muda repentinamente, a função de onda pela esquerda e pela direita se juntam no mesmo ponto.
Ela ser suave significa que a mesma coisa vale pra sua derivada.
Passo 3
Letra c)
Substituindo as condições de contorno do passo anterior, ficamos com:
Uma observação: A solução mais geral de fato para a região seriam exponenciais complexas. Porém, exponenciais complexas podem ser relacionadas com senos e cosenos, bastando usar constantes complexas.
Como tem muito “complexo” na frase de cima, decidimos fazer “simples” e ir direto pra seno e coseno. O resultado final é equivalente.
Resposta
Letra
Letra
Letra