Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Deslocamento em estruturas isostáticas- Temperatura e Recalque.

Ver Teoria
Exercício 21345678

Enunciado

Uma treliça possui as fibras da parte superior com uma temperatura de 80°C e da parte inferior com 10°c. sabendo disso determine o deslocamento vertical o ponto E. use:

E J = 50   .   10 5

s e ç ã o   d a   v i g a = 30   c m   d e   a l m a   p o r   90   c m   d e   a l t u r a   ( v i g a   r e t a n g u l a r )

α = 1.10 - 3 ° C - 1

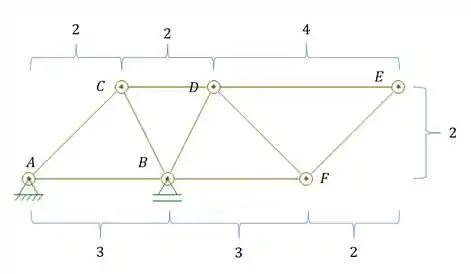
Passo 1

sabemos que para calculo da temperatura usamos a seguinte equação:

P ¯ δ = ∫ N ¯ α t g d s + ∫ M ¯ α ∆ t h d s

Que podemos simplificar de acordo como o tipo de estrutura, no nosso caso como se trata de uma treliça, podemos descartar a contribuição de momentos, e ficar apenas com a contribuição de normais. Dessa maneira teremos que a nossa fórmula será.

P ¯ δ = ∫ N ¯ α t g d s

Sabemos que a temperatura no centro de gravidade da peça e o coeficiente de dilatação térmico são constantes na nossa fórmula, logo podemos escrever a mesma da seguinte maneira.

P ¯ δ = α t g ∫ N ¯ d s

E sabemos que a integral do normal devido a carga unitária, integrado no comprimento S de cada uma das barras de treliça, nada mais é que a área do diagrama, ou seja, nossa fórmula passa a ser.

P ¯ δ = α t g ∑ A N i

Em que:

∑ A N i = s o m a t ó r i o   d a s   á r e a s   d o   d i a g r a m a   d e   n o r m a i s   d e   c a d a   u m a   d a s   b a r r a s

Passo 2

como podemos ver o que falta é exatamente o diagrama de momentos devido a carga unitária posicionada no ponto em que queremos saber o deslocamento, na direção em que queremos saber o deslocamento. Dessa maneira teremos que:

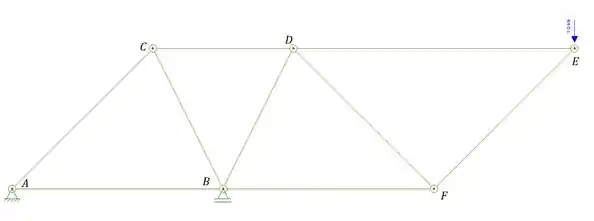
Desenhando o diagrama de cada uma das barras teremos que:

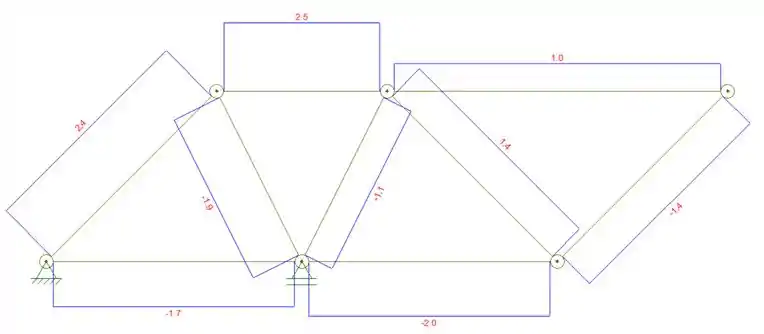
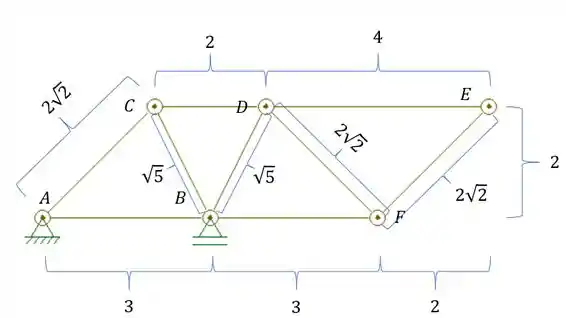
Para o cálculo da área precisamos do comprimento de cada uma das barras, que podemos calcular por Pitágoras e com isso teremos que:

Agora calculamos o somatório das áreas (tome cuidado de manter os sinais):

∑ A N i = 2,4   .   2 2 - 1,7   .   3 - 1,9   .   5 - 1,1 . 5 + 2,5   .   2 - 2   .   3 + 1,4   .   2 2 + 1   .   4 - 1,4   .   2 2 = - 2 , 0

Passo 3

Precisamos por fim determinar a temperatura no centro de gravidade da seção retangular. Sabemos que o centro de gravidade da seção retangular é no meio da seção, sendo assim a temperatura será dada por:

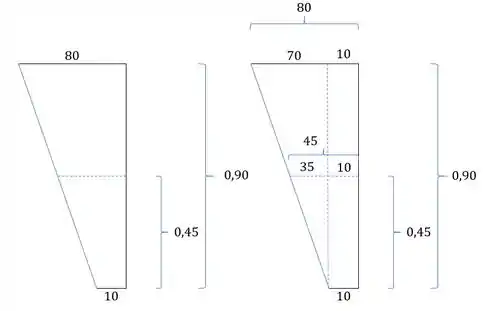
Logo a temperatura no centro de gravidade da seção é de 45°C

Passo 4

Agora é substituir os termos na nossa fórmula

P ¯ δ = α t g ∑ A N i

P ¯ = 1   k N

α = 1.10 - 3 ° C - 1

t g = 45 ° C

∑ A N i = - 2,02   m

Substituindo teremos que:

1 . δ = 1.10 - 3 . 45 . - 2,0 = - 0,09   m

δ = - 90   m m

Vale lembrar que colocamos nossa carga unitária para baixo contando da estrutura deformar para baixo, porém podemos ver que a deformação deu negativa, logo, a estrutura deforma na outra direção, ou seja, pra cima.

Resposta

δ = - 90   m m