Exercícios de Fluxo Concatenado e Indutância - Lista de Exercícios Resolvida

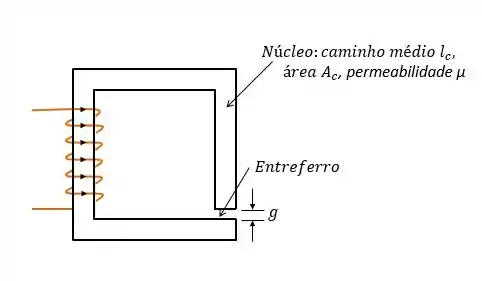
O indutor abaixo tem as seguintes dimensões:

Desprezando os campos de espraiamento no entreferro e de dispersão e supondo , calcule a indutância.

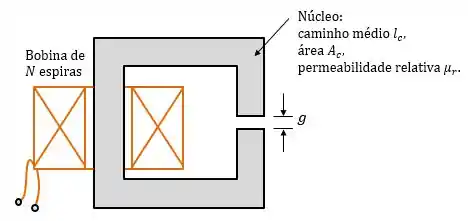
O circuito magnético abaixo tem dois enrolamentos e dois entreferros. Pode-se supor que o núcleo tenha permeabilidade infinita. As dimensões do núcleo são indicadas na figura.

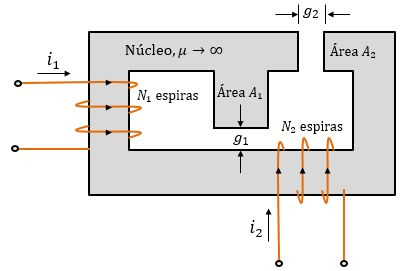
Suponha que a bobina esteja conduzindo uma corrente e a corrente na bobina seja zero, calcule a densidade de fluxo magnético em cada um dos entreferros, o fluxo concatenado do enrolamento e o fluxo concatenado do enrolamento .

Repita a parte , supondo uma corrente zero no enrolamento e uma corrente no enrolamento .

Repita a parte , supondo que a corrente do enrolamento seja e a corrente do enrolamento seja .

Encontre as indutâncias próprias dos enrolamentos e , e a indutância mútua entre os enrolamentos.

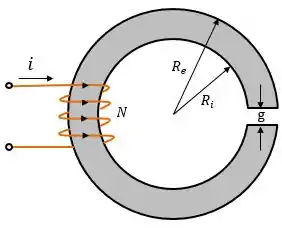
O circuito magnético abaixo consiste em anéis de material magnético dispostos em uma pilha de altura . Os anéis têm raio interno e externo . Suponha que o ferro tenha permeabilidade infinita , e despreze os efeitos de dispersão e de espraiamento magnéticos. Para:

Calcule:

O comprimento médio do núcleo e a área da seção reta

A relutância do núcleo e a do entreferro .

Para espiras, calcule:

a indutância .

A corrente requerida para que se opere com uma densidade de fluxo no entreferro de .

O fluxo concatenado correspondente a da bobina.

Um indutor deve ser projetado usando um núcleo magnético com a forma dada pela figura abaixo:

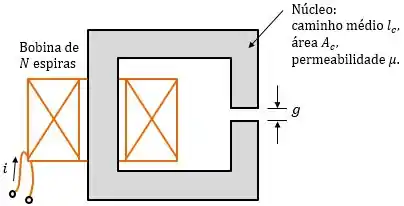
O núcleo tem seção reta uniforme de área e comprimento médio . Calcule o comprimento do entreferro e o número de espiras tais que a indutância seja e de modo que o indutor possa operar com corrente de pico de sem saturação. Suponha que a saturação ocorra quando a densidade de fluxo de pico do núcleo exceda a e que, abaixo da saturação, o núcleo tenha permeabilidade .

Um circuito magnético com um único entreferro está mostrado na figura abaixo. As dimensões do núcleo são:

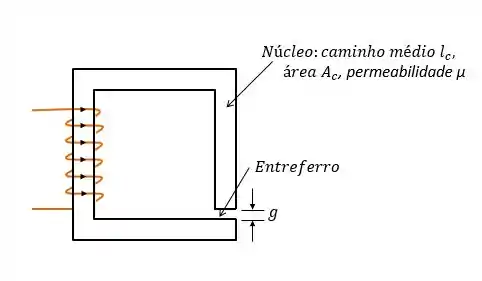
Área da seção reta

Comprimento médio do núcleo

Comprimento do entreferro

espiras

Suponha que o núcleo tenha permeabilidade infinita e despreze os efeitos dos campos de fluxo disperso e os de espraiamento no entreferro.

Calcule a relutância do núcleo e a do entreferro .

Para uma corrente de , calcule:

O fluxo total ;

O fluxo concatenado da bobina;

a indutância da bobina.

Um circuito magnético com um único entreferro está mostrado na figura abaixo. As dimensões do núcleo são:

Área da seção reta

Comprimento médio do núcleo

Comprimento do entreferro

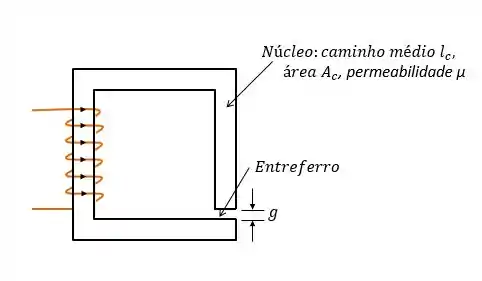
Supondo uma permeabilidade de núcleo infinita , calcule:

O número necessário de espiras para obter uma indutância de .

A corrente no indutor que resultará em uma densidade de fluxo de .

Um indutor com a forma da figura abaixo tem as dimensões:

Área da seção reta

Comprimento médio do núcleo

espiras

Supondo uma permeabilidade de núcleo de e desprezando os efeitos do fluxo disperso e dos campos de espraiamento, calcule o comprimento de entreferro necessário para se obter uma indutância de .