O circuito magnético abaixo tem dois enrolamentos e dois entreferros. Pode-se supor que o núcleo tenha permeabilidade infinita. As dimensões do núcleo são indicadas na figura.
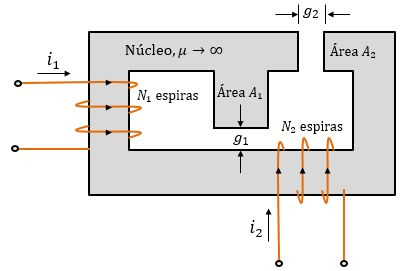
Suponha que a bobina esteja conduzindo uma corrente e a corrente na bobina seja zero, calcule a densidade de fluxo magnético em cada um dos entreferros, o fluxo concatenado do enrolamento e o fluxo concatenado do enrolamento .
Repita a parte , supondo uma corrente zero no enrolamento e uma corrente no enrolamento .
Repita a parte , supondo que a corrente do enrolamento seja e a corrente do enrolamento seja .
Encontre as indutâncias próprias dos enrolamentos e , e a indutância mútua entre os enrolamentos.
Passo 1
Esse circuito magnético é um pouco complicado de se analisar diretamente. Então, vamos utilizar a analogia entre circuitos magnéticos e elétricos e desenhar o circuito associado a esse problema.
Como a permeabilidade do núcleo é infinita, sua relutância é zero. Então, vamos considerar apenas as relutâncias do entreferro. Além disso, devido aos dois enrolamentos teremos duas . Portanto, desenhando o circuito temos:
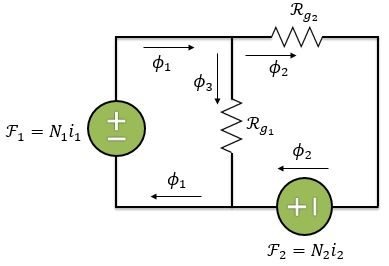
Onde as relutâncias dos entreferros são:
Passo 2
Na letra a bobina tem uma corrente e . Logo, , o que significa que podemos substituí-la por um curto-circuito.
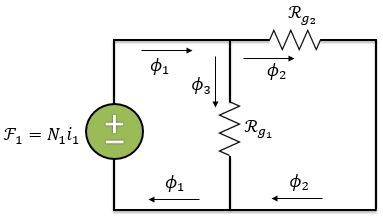
Primeiro, temos que determinar a densidade de fluxo em cada entreferro. A densidade de fluxo do primeiro entreferro pode ser calculada pela divisão entre o fluxo que passa por ele e a área da sua seção reta :
Pela analogia entre circuitos elétricos e magnéticos, sabemos que:
Logo, o fluxo que passa pelo primeiro entreferro pode ser determinado assim:
Como
Substituindo:
Passo 3
Então, substituindo o valor encontrado para o fluxo, a densidade no primeiro entreferro será:
Passo 4
Da mesma forma, no segundo entreferro teremos:
A segunda relutância está em paralelo com a primeira. Logo, nela também está sendo aplicada a mesma .
Então, substituindo o valor encontrado para o fluxo, a densidade no segundo entreferro será:
Passo 5
No item , temos que determinar o fluxo concatenado do enrolamento . Pela definição, o fluxo concatenado é o produto entre o número de espiras da bonina e o fluxo que passa por essa bobina. Então, para a bobina , temos:
Analisando o nó do nosso circuito, temos que
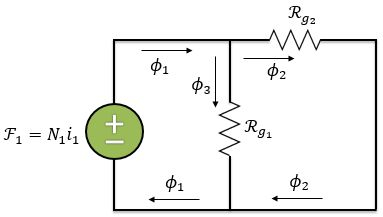
Logo, o fluxo concatenado da primeira bobina será:
Substituindo os fluxos pelos seus valores que determinamos anteriormente:
Passo 6
Da mesma forma, no item , o fluxo concatenado da bobina é
Como
Temos:
Passo 7
Agora, vamos fazer a mesma análise para a letra . Para essa letra, e na bobina circula uma corrente . Logo, podemos substituir por um curto-circuito a fonte e analisar o circuito abaixo:
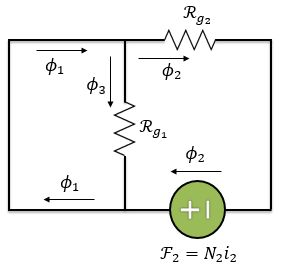
Nesse caso o fluxo que passa pelo primeiro entreferro é zero, já que todo o fluxo produzido pela passará pelo curto-circuito. Logo:
Como , a densidade de fluxo no primeiro entreferro é zero.
Passo 8
No segundo entreferro teremos:
Como analisamos, podemos desconsiderar , já que não passa fluxo algum por ela. Então, podemos reduzir nosso circuito:
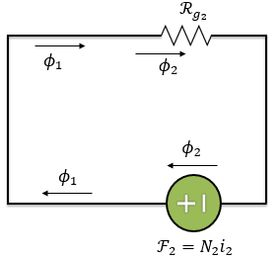
Então, temos o circuito mais simples possível, com uma fonte em série com uma relutância, e o fluxo que passa pelo segundo entreferro é
Então, substituindo o valor encontrado para o fluxo, a densidade no segundo entreferro será:
Passo 9
Agora, vamos fazer o item . O fluxo concatenado do enrolamento é definido como:
Como , temos:
Passo 10
Já no item temos que determinar o fluxo concatenado da segunda bobina.
Substituindo:
Passo 11
Agora, na letra , ambos os enrolamentos possuem corrente. Logo, temos que considerar as duas .
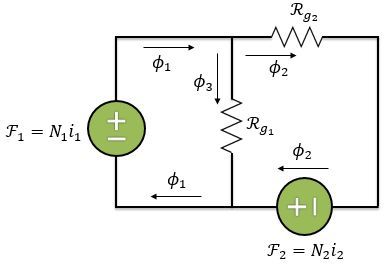
Como a relutância do primeiro entreferro está ligada em paralelo com , temos:
Então, substituindo o valor encontrado para o fluxo, a densidade de fluxo no primeiro entreferro será:
Passo 12
Da mesma forma, no segundo entreferro teremos:
Agora temos que ter cuidado ao calcular , já que não está ligada diretamente a relutância. Então, vamos usar um método de análise que já conhecemos de circuitos elétricos: o método da superposição.
Vamos considerar a contribuição de cada fonte para gerar o e depois soma-las. Então:
Onde é a contribuição da fonte e é a contribuição da fonte .
Pelo método da superposição, quando queremos determinar a contribuição de uma das fontes temos que desligar a outra. Logo, como as fontes são análogas às fontes de tensão, desliga-las é o mesmo que substituí-las por um curto-circuito.
Considerando apenas a primeira fonte temos o circuito abaixo:
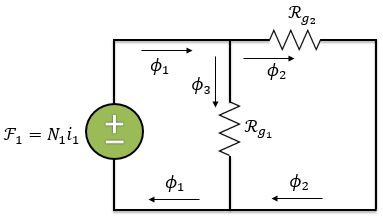
Esse é o mesmo circuito que analisamos na letra , está lembrado?
Para esse circuito:
Passo 13
Agora vamos considerar apenas a segunda fonte:
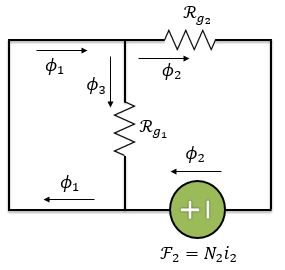
Esse é o mesmo circuito que utilizamos na letra . Como tínhamos analisado, podemos desconsiderar , já que não passa fluxo algum por ela, e reduzir nosso circuito:
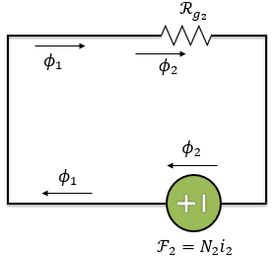
Então, o fluxo que passa pelo segundo entreferro é
Portanto, o fluxo total que passa pelo segundo entreferro será:
Passo 14
Então, substituindo o valor encontrado para o fluxo, a densidade no segundo entreferro será:
Passo 15
Agora, vamos fazer o item . O fluxo concatenado do enrolamento é definido como:
Analisando o nó do nosso circuito, temos que
Logo:
Passo 16
Já no item temos que determinar o fluxo concatenado da segunda bobina.
Substituindo:
Passo 17
Estamos quase terminando! Na letra temos que determinar as indutâncias próprias dos enrolamentos e , e a indutância mútua entre os enrolamentos. Vamos começar pelo primeiro enrolamento.
A fórmula que relaciona fluxo concatenado e indutância é essa:
Onde é a indutância própria do enrolamento e é a indutância mútua entre os enrolamentos.
Na letra , tínhamos calculado o fluxo concatenado da primeira bobina:
Comparando com
Vemos que a indutância própria do enrolamento é toda expressão que está multiplicando a corrente e a mútua é a expressão que está multiplicando a corrente da outra bobina.
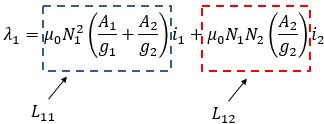
Logo,
E
Passo 18
Agora vamos fazer a mesma análise para a bobina .
Onde é a indutância mútua e é a indutância própria do segundo enrolamento.
Na letra , tínhamos calculado o fluxo concatenado da segunda bobina:
Comparando com
Vemos que a indutância própria do enrolamento é toda expressão que está multiplicando a corrente e a mútua é a expressão que está multiplicando a corrente da outra bobina.
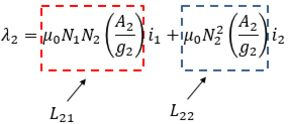
Logo,
E