Associação de resistores
Produzido por Alexandre NunesTeoria
Fala, galera!
Já viu um circuito com vários resistores assim:
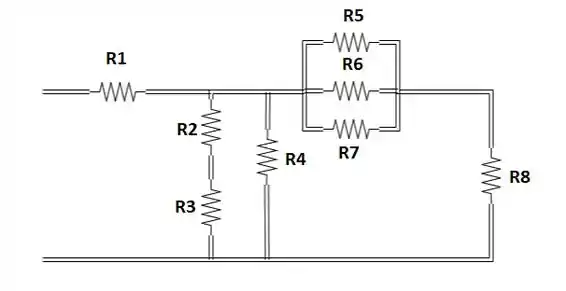
Relaxa, ele parece grande, mas vamos ver como reduzir ele em até um resistor.
Série
A primeira associação é a série. Dois resistores estão em série, quando eles possuem apenas um nó em comum:
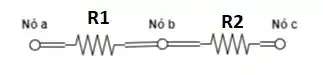
Nesse caso, o nó em comum para os resistores e é o nó b.
Olhando a figura abaixo, os resistores e estão em série, portanto a mesma corrente flui pelos dois resistores.
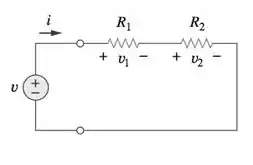
Portanto, as quedas de tensão em cada resistor são:
Utilizando a LKT, temos o laço:
Com isso podemos concluir que a Resistência equivalente é:
Podemos assim simplificar o circuito da seguinte forma:
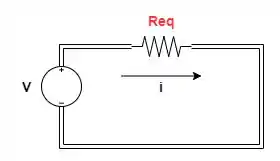
A associação em série é igual ao somatório de todos os resistores em série:
Esse processo de associação pode ser simplificado associando de dois em dois resistores de cada vez.
Paralelo
A outra associação de resistores possível, é a paralelo.
Dois ou mais resistores estão em paralelo quando possuem seus dois nós em comum:
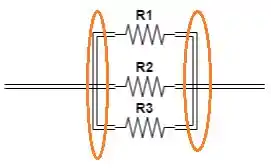
Nesse caso, os resistores , e são conectados entre os mesmos dois pontos (nós), logo estão em paralelo.
Olhando para o circuito abaixo e percebemos que e estão associados em paralelo.
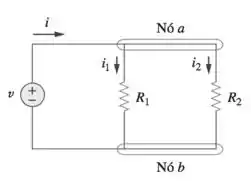
Percebemos que na configuração de associação em paralelo, as correntes são diferentes que entram em cada resistor e a queda de tensão é a mesma em cima dos resistores.
Como não temos nenhuma queda de tensão antes dos resistores e , a tensão aplicada pela fonte é igual a queda de tensão nos resistores:
E pela LKC no nó a, sabemos que a soma das correntes que entram é igual a soma das correntes que saem do nó:
Concluindo então que a Resistência equivalente do circuito é:
Um outro jeito de mostrar a equivalente, caso você sempre associe de dois em dois é,
Após isso, podemos substituir esse circuito por esse circuito mais simples:
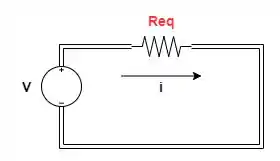
Uma dica muuuuito importante é: sempre faça as associações vindo da parte mais distante da fonte em direção a mais próxima da fonte de tensão.
Bom, agora que vimos esses dois tipos de associação, é bem provável que em algum circuito que pegue para resolver exista as duas associações juntas, para que não se perca na resolução do exercício, sempre lembre de associar de dois em dois resistores.
Para fica bom mesmo, agora só praticando, então: Borá lá exercitar.