Fontes de Tensão e de Corrente e Instrumentos de Medição
Produzido por Alexandre NunesTeoria
Opaa, seja bem vindo ao Responde Aí! Bora bater um papo sobre Fontes de Tensão e de Corrente?!
Fontes de Tensão
A tensão nada mais é do que a diferença de potencial entre dos pontos. Em um circuito uma fonte de tensão pode ser uma pilha, uma bateria, ou até um regulador de tensão por exemplo. Elas são representadas assim:
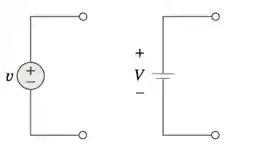
Esse componente é responsável por manter constante ou alterar a diferença de potencial entre dois pontos do circuito. Ou seja, as fontes de tensão podem ser independentes ou dependentes. As fontes independentes liberam a corrente necessária para que a tensão permaneça a mesma com o passar do tempo.
Nas fontes de tensão independentes não tem mistério, se o seu exercício diz que a tensão do circuito é igual a
As fontes dependentes podem variar a tensão em função de um outro elemento do circuito, como corrente e resistência. Se liga nesse exemplo aqui:
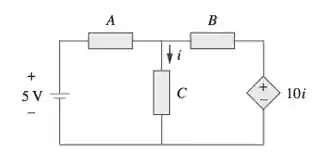
Nesse caso a tensão da fonte é igual a
Ahh…reparou que o em volta da fonte tem um losango?! Sempre que a fonte for representada dessa forma, estamos falando de uma fonte dependente! 😉
📢 Clique para saber mais:
- Fontes de Tensão e Corrente: Exercícios Resolvidos
- Fonte Reguladora de Tensão
- Fórmulas das Leis de Ohm
Fontes de Corrente
Também existem dois tipos de fontes de corrente, as dependentes e as independentes! As fontes independentes para corrente liberam a tensão necessária no circuito para conseguir manter a corrente constante.
Podemos reconhecer uma fonte de corrente independente pelo seu símbolo no circuito:
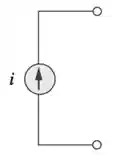
Já nas fontes de corrente dependentes, o valor da corrente da fonte depende de outra variável do circuito, como uma corrente ou uma tensão em um elemento. Como por exemplo:
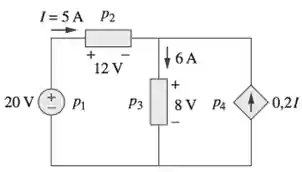
Como nesse circuito sabemos que a corrente
Você pode perceber que o símbolo da fonte de corrente dependente é diferente que o símbolo da fonte independente:
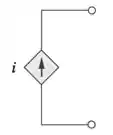
Instrumentos de Medição
No dia a dia são usados instrumentos de medição para saber a tensão, a corrente e a resistência de um circuito! Agora vamos conhecer esses circuitos melhor!
Voltímetro
O voltímetro é um instrumento utilizado para medir a tensão entre dois pontos de um circuito. Para que a resistência do voltímetro não influencie no circuito, fazendo com que mude a corrente e com isso a tensão nos pontos medidos, a resistência interna de um voltímetro é considerada infinita. Para medir uma queda de tensão, em uma resistência de um circuito, é preciso conectar um voltímetro em paralelo à resistência.
Amperímetro
O amperímetro é o instrumento responsável por medir corrente de um circuito. Ao contrário do voltímetro, a resistência do amperímetro é nula. Portanto, o amperímetro é conectado em série com o restante do circuito que está medindo a corrente.
Ohmímetro
O ohmímetro é o instrumento que mede qual o valor da resistência em Ohms (Ω). Ele é adicionado em paralelo com a resistência, igual ao voltímetro, porém para medir o valor dela, é necessário que retire do circuito, pois se não irá medir a resistência do circuito inteiro.
Multímetro
Agora que já vimos os principais instrumentos de medição, vou mostrar para vocês um que contém todos eles em um só equipamento, o multímetro! O multímetro tem internamente um circuito com voltímetro, amperímetro, ohmímetro, e mais umas funções adicionais que depende do multímetro que você tem.
Instrumentos de Medição
Exercícios Resolvidos
Exercício Resolvido #1
Fundamentos de Circuitos Elétricos – 5ª Edição – Charles K. Alexander, Mathew N.O. Sadiku – Exercício 2.9
Qual dos circuitos da figura fornecerá .
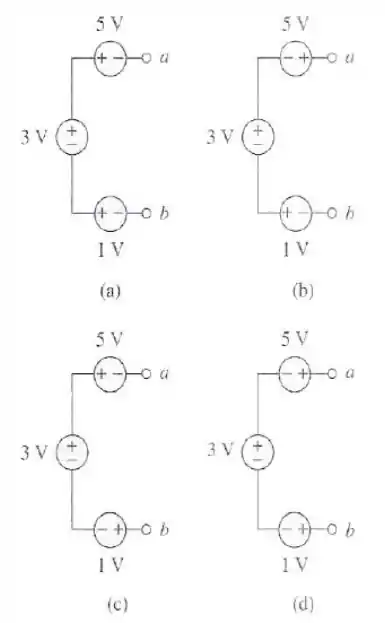
Passo 1
O enunciado está interessado no valor de , portanto, iremos percorrer um caminho que vai do ponto ao ponto , certo?
Lembrando que quando nos depararmos com o terminal negativo da fonte, temos uma tensão negativa, e se nos depararmos com o terminal positivo, a tensão é positiva.
Vamos então um por um.
Passo 2
Na letra (a), temos que:
Já na letra (b), temos:
Na (c):
E na letra (d):
Portanto, temos que a reposta que nos dá é a configuração da letra (d).
Resposta
(d)
Exercício Resolvido #2
Fundamentos de Circuitos Elétricos – 5ª Edição – Charles K. Alexander, Mathew N.O. Sadiku – Problema 2.16
Determine no circuito da figura.
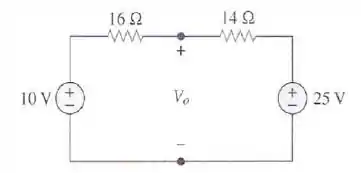
Passo 1
Esta questão é um pouco tricky, mas vamos lá. Primeiro vamos percorrer o caminho do pro e encontrar os dois valores de em função da corrente que passa pelo circuito, que é a mesma para os dois lados do circuito, certo?
Antes disso, precisamos definir o sentido da corrente que passa por esse circuito, vamos escolher arbitrariamente o sentido horário, e os terminais dos resistores ficarão assim:
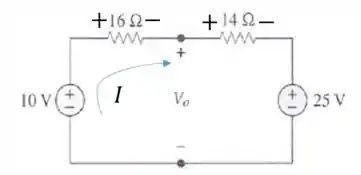
Passo 2
Percorrendo o caminho no braço esquerdo:
Já no braço direito:
Se igualarmos as duas expressões para , temos:
E então:
Passo 3
Agora basta substituir esse valor de em uma das equações para encontrar o valor de :
Resposta
Exercício Resolvido #3
Circuitos RC
O amperímetro marca . Determine os valores de e .
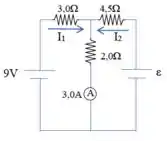
Passo 1
Para resolver esse circuito, vamos usar a lei das malhas. Vamos considerar a primeira malha, a malha da esquerda e a segunda malha, a da direita.
Pela lei dos nós, já sabemos que , pois essa é a corrente no ramo em que as correntes se somam.
Na primeira malha, adotando o sentido da corrente temos:
Portanto, temos que:
Agora que já temos os valores das correntes, basta analisar a segunda malha para determinar .
Passo 2
Analisando a segunda malha, no sentido da corrente, temos:
Resposta
Exercício Resolvido #4
Fundamentos de Circuitos Elétricos – 5ª Edição – Charles K. Alexander, Mathew N.O. Sadiku – Problema 2.15
Determine e , no circuito da figura.
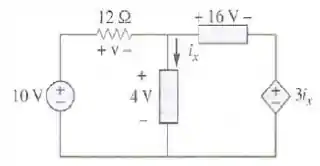
Passo 1
Vamos primeiramente encontrar o valor de , para isso vamos usar o fato de os dois ramos da esquerda do circuito tem a mesma diferença de tensão.
Portanto, usando a primeira lei de Ohm e percorrendo os dois caminhos, o do ramo central e o do ramo da esquerda:
Portanto:
Passo 2
Podemos fazer a mesma coisa pro ramo da direita:
Resposta
Exercício Resolvido #5
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2006, pp 193-49.
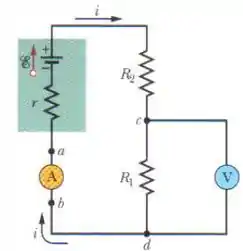
Na figura abaixo suponha que . Se a resistência do voltímetro é que erro percentual o voltímetro introduz na medida da diferença de potencial entre os terminais de ? Ignore a presença do amperímetro.
, 
Passo 1
Aqui temos mais um circuito com mais de uma malha. Logo, de cara já sabemos que teremos que usar as Leis de Kirchhoff, tanto nos nós quanto nas malhas.
O erro percentual no potencial pode ser calculado pela divisão entre a ddp gasta pelo resistor se ele tivesse com ou sem voltímetro ligado em paralelo, e pra poder calcular isso temos que achar o valor da corrente nos dois casos. Vamos procurá-la
Passo 2
Aplicando a Lei de Kirchhoff na malha da esquerda utilizando a direção de corrente dada, teremos:
Já aplicando na malha da direita, teremos:
Passo 3
Mas ah, pela Lei dos nós no nó C, teremos:
Substituindo na ultima equação do passo anterior, vai ficar:
Agora substituindo na primeira equação, vamos ter:
Passo 4
Achando o potencial entre os terminais do resistor , vamos ter:
Passo 5
Se não houvesse o voltímetro, teríamos uma malha única e a corrente seria apenas , calculada, usando a Lei das Malhas, por:
E o potencial seria calculado por:
Logo, o erro percentual vai ser calculado pela diferença percentual entre esses dois valores, dado por:
Resposta
Exercício Resolvido #6
Fundamentos de Circuitos Elétricos – 5ª Edição – Charles K. Alexander, Mathew N.O. Sadiku – Problema 2.20
Determine no circuito da figura.
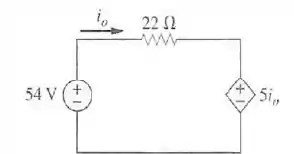
Passo 1
Vamos pegar os dois terminais da fonte dependente, sabemos que a diferença de tensão entre estes terminais é a mesma tanto se usarmos o ramo da própria fonte dependente como se usarmos o ramo que vai pra esquerda, certo?
Portanto:
Resolvendo:
Resposta
Exercício Resolvido #7
Fundamentos de Circuitos Elétricos – 5ª Edição – Charles K. Alexander, Mathew N.O. Sadiku – Problema 2.21
Determine no circuito da figura.
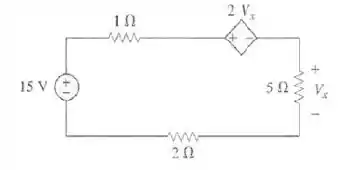
Passo 1
Para encontrar o valor de , podemos percorrer o circuito pelo ramo da esquerda e igualar a , mas para isso temos que definir um sentido para corrente, vamos arbitrar o sentido horário e então fica assim:
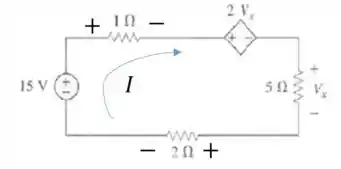
Vamos andar do terminal negativo de , e então acharemos o valor de :
Simplificando:
Já no ramo da resistência de :
Passo 2
Juntando as duas equações:
Resposta
Exercício Resolvido #8
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2006, pp 194-51. Modificada
Na figura abaixo, determine a leitura do amperímetro para (fonte ideal) , .
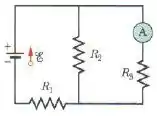
Passo 1
Se ele está nos pedindo a medição do amperímetro, ele está pedindo a corrente que passa ali, certo?
Então o que temos que fazer é calcular a corrente que passa naquele ramo! #VamoQueVamo!
Passo 2
A corrente sempre vai do menor para o maior potencial, logo o sentido da corrente será esse aqui, oh!
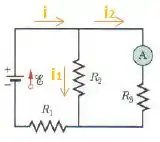
Passo 3
Aplicando a Lei dos Nós no nó em cima de , teremos:
Tranquilo até aí, né?
Agora aplicando a Lei das Malhas, teremos:
Na da esquerda:
Na da direita:
Passo 4
Beleza, 3 equações, 3 incógnitas, agora é só resolver o sisteminha!
Aplicando agora na equação da malha da esquerda, vamos ter:
Passo 5
A gente descobriu lá na Lei das Malhas na direita, que:
Logo
Resposta
A leitura do amperímetro é dada por .
Exercício Resolvido #9
Boylestad – 12 ed. – Capítulo 6 - Exercício 8
Converta a fonte de tensão em fonte de corrente do circuito:
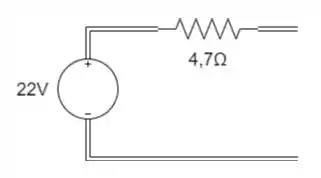
Passo 1
Podemos substituir uma fonte de corrente em paralelo com um resistor por uma fonte de tensão em série com o mesmo resistor. Para isso devemos calcular o valor da fonte de corrente:
Passo 2
Assim podemos redesenhar o circuito equivalente:
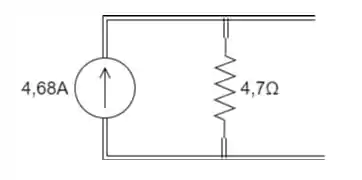
Resposta
Exercício Resolvido #10
Boylestad – 12 ed. – Capítulo 6 - Exercício 8
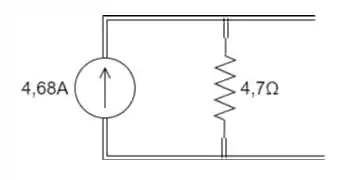
Converta a fonte de corrente em fonte de tensão do circuito:
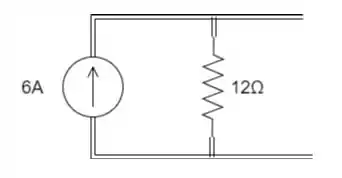
Passo 1
Podemos substituir uma fonte de corrente em paralelo com um resistor por uma fonte de tensão em série com o mesmo resistor. Para isso devemos calcular o valor da fonte de tensão:
Passo 2
Assim podemos redesenhar o circuito equivalente:
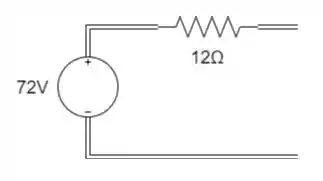
Resposta