Lei de Kirchhoff
Produzido por Alexandre NunesTeoria
Existem duas leis de Kirchhoff, a Lei dos Nós e Lei das Malhas e elas são usadas para encontrar a intensidade da corrente elétrica em circuitos elétricos que não podem ser reduzidos a circuitos simples.
Se liga esse vídeozinho com tudo o que você precisa saber sobre as Leis de Kirchhoff para arrasar na prova 👇
Ou continua comigo no textinho! 👇
1° Lei de Kirchhoff: Lei dos Nós
Antes de qualquer coisa, o que são nós?
Os nós são pontos do circuito nos quais a corrente se divide. Se liga nessa imagem:
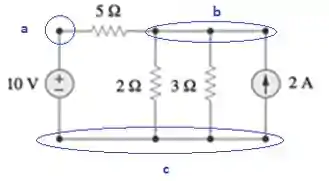
Na figura acima nó
Beleza, agora que já sabemos o que são os nós, podemos ir pra primeira lei de Kirchhoff!
A lei dos nós diz que a soma de todas as correntes que entram em um nó deve ser igual a soma de todas correntes que saem desse mesmo nó.
Olha esse exemplo na imagem abaixo:
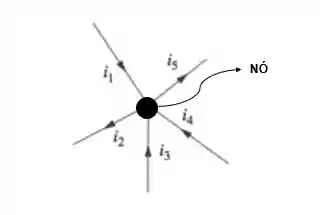
A gente consegue ver que as correntes
Lei dos Nós - Exemplo
Imagina que sabemos 3 das correntes que passam pelo nó "b" (
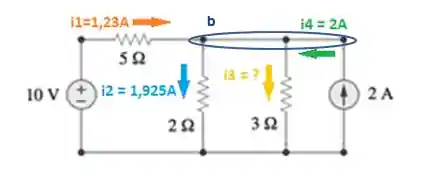
Para sabermos o valor da corrente
Primeiro precisamos identificar correntes que estão saindo e as correntes que estão entrando no nó "b".
Aplicando a lei de Kirchhoff temos:
Protinho, achamos o valor da corrente
2° Lei de Kirchhoff: Lei das Malhas
As malhas são caminhos fechados em um circuito, em que iniciamos em um nó, percorremos um caminho sem passar pelo mesmo nó mais de uma vez, e voltamos ao mesmo nó inicial.
Se liga nessa imagem:
A lei das malhas diz que para a soma dos potenciais elétricos ao longo de uma malha fechada é igual a zero. Matematicamente podemos escrever assim:
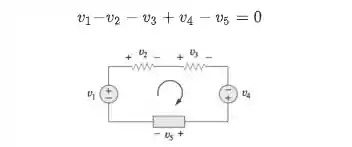
Lei das Malhas - Exemplo
Para a malha destacada na figura abaixo, sabemos o potencial elétrico de dois dos elementos que a compõe. Calcule o valor de
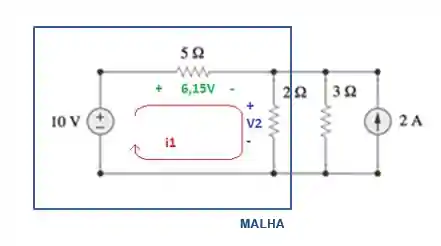
Primeiramente, vamos adotar como sentido da nossa análise o sentido da corrente.
Com o sentido adotado, podemos aplicar a lei:
-Como eu sei qual potencial é negativo e qual é positivo?
É simples: Quando a corrente entra pelo polo negativo e sai pelo polo positivo, temos uma tensão positiva. Por outro lado, quando a corrente entra pelo polo positivo e sai pelo negativo temos uma tensão negativa.
Agora é só partir pros exercícios 😉
2° Lei de Kirchhoff: Lei das Malhas
Exercícios Resolvidos
Exercício Resolvido #1
A corrente na figura é:
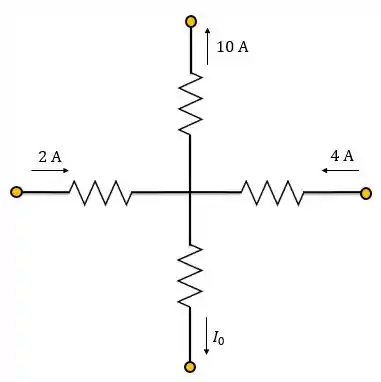
Passo 1
Vamos aplicar a lei das correntes de Kirchhoff. Lembrando que a soma das correntes que entram no nó é igual a soma das correntes que saem do nó, temos:
A corrente negativa significa que o sentido da corrente real é o contrário do que tínhamos pensado inicialmente, logo a corrente deveria estar no sentido real de acordo com o seguinte desenho para ser positiva:
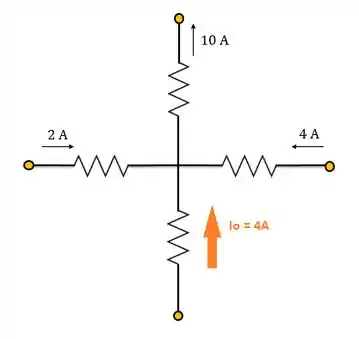
Faz sentido né? Agora conseguimos igualar a soma das correntes que entram com a soma das correntes que saem.
Resposta
Exercício Resolvido #2
A corrente no circuito da figura é:
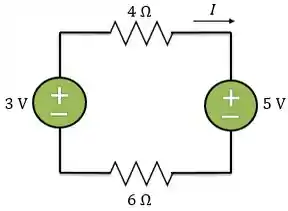
Passo 1
Pela lei de Ohm, sabemos que quando uma corrente passa pelo resistor ela gera uma queda de tensão nesse resistor. Então, temos as seguintes quedas de tensão nos resistores:
Passo 2
Agora, vamos aplicar a lei Kirchhoff das tensões na malha abaixo:
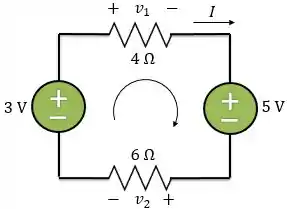
Adotando o sentido horário e lembrando que quando a corrente entra pelo polo positivo contamos como uma queda de tensão negativa e quando entra pelo polo negativo consideramos como uma tensão positiva, temos:
Passo 3
Substituindo os valores das tensões:
Resposta
Exercício Resolvido #3
Determine , e no circuito da figura.
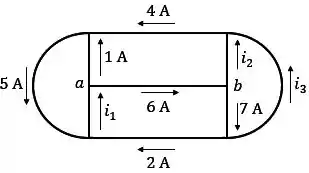
Passo 1
Vamos determinar as correntes utilizando a lei de Kirchhoff das correntes (LKC). Basicamente, temos que lembrar que a soma das correntes que entram em um nó é igual à soma das correntes que saem do nó.
Passo 2
Aplicando a LKC ao nó , temos:
Agora ao nó :
Passo 3
Falta encontrarmos . Para isso, vamos aplicar a LKC ao nó amarelo do circuito abaixo:
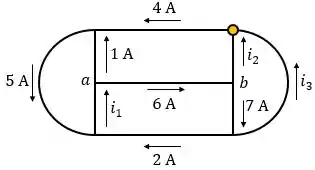
Como ,
Resposta
Exercício Resolvido #4
Determine e no circuito da figura abaixo:
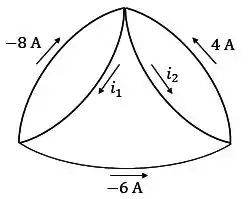
Passo 1
Vamos determinar as correntes utilizando a lei de Kirchhoff das correntes (LKC). Basicamente, temos que lembrar que a soma das correntes que entram em um nó é igual à soma das correntes que saem do nó.
Passo 2
Nomeando os dois nós inferiores como no circuito abaixo:
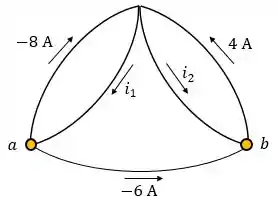
Aplicando a LKC ao nó , temos:
Agora, aplicando ao nó :
Resposta
Exercício Resolvido #5
No circuito abaixo, determine e .
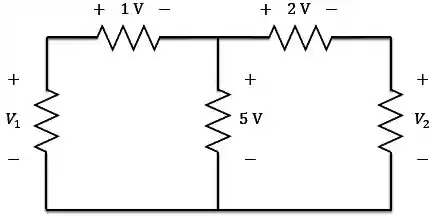
Passo 1
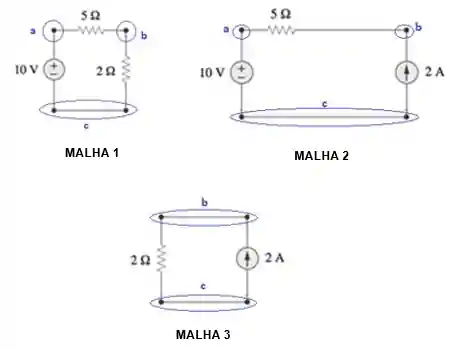
Esse circuito possui duas malhas fechadas:
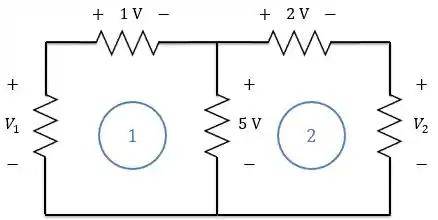
Para encontrarmos as tensões e , vamos utilizar a lei Kirchhoff das tensões.
Passo 2
Agora, vamos aplicar a lei Kirchhoff das tensões nas malhas do circuito abaixo:
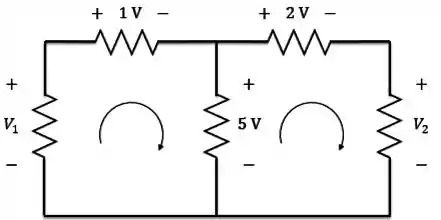
Adotando o sentido horário e lembrando que o sinal de tensão em cada elemento do circuito é dado pelo primeiro sinal que encontramos à medida que percorremos o circuito, temos:
Da malha 1:
Da malha 2:
Resposta
Exercício Resolvido #6
No circuito abaixo, calcule , e .
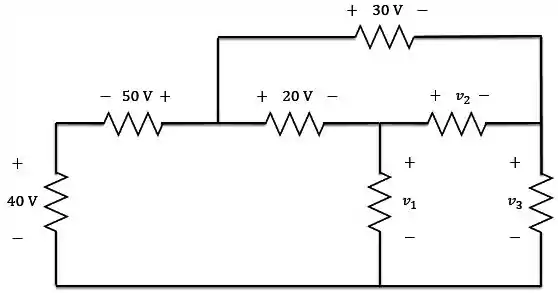
Passo 1
Vamos começar! Esse circuito possui três malhas fechadas:
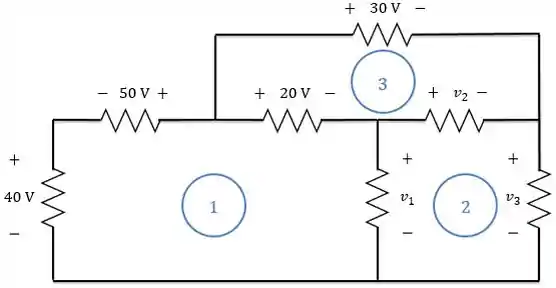
Para encontrarmos as tensões , e , vamos utilizar a lei Kirchhoff das tensões.
Passo 2
Agora, vamos aplicar a lei Kirchhoff das tensões nas malhas do circuito abaixo:
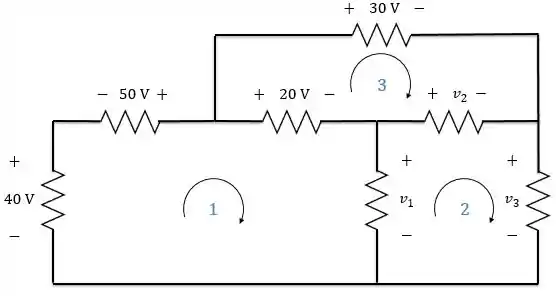
Adotando o sentido horário e lembrando que o sinal de tensão em cada elemento do circuito é dado pelo primeiro sinal que encontramos à medida que percorremos o circuito, temos:
Da malha 1:
Da malha 2:
Da malha 3:
Passo 3
Substituindo os valores encontrados para e na expressão da malha 2, temos:
Resposta
Exercício Resolvido #7
Para o circuito da figura, use a LKC para encontrar as correntes nos ramos a .
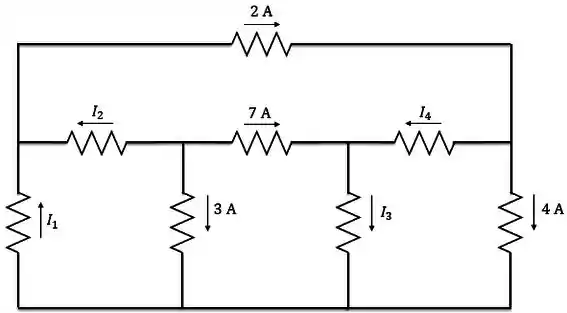
Passo 1
Nesse circuito temos quatro nós:
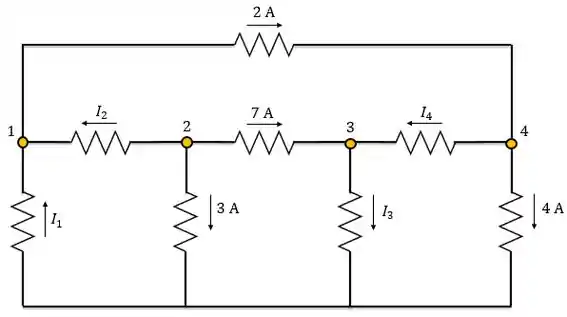
Para encontrarmos as correntes de cada ramo vamos aplicar a lei das correntes de Kirchhoff. Lembrando que essa lei diz que a soma das correntes que entram no nó é igual à soma das correntes que saem do nó.
Passo 2
Agora vamos começar a aplicar a LKC. Aplicando ao nó 1, temos:
Agora ao nó 2:
Nó 3:
Nó 4:
Passo 3
Substituindo os valores de e nas outras equações encontramos os valores de e .
Resposta
Exercício Resolvido #8
Boylestad – 12 ed. – Capítulo 6 - Exercício 24
Usando a Lei de Kirchhoff para corrente, determine as correntes desconhecidas para o circuito em paralelo na figura:
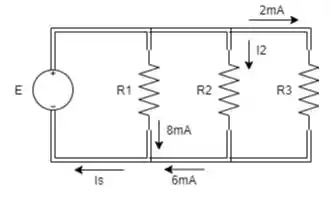
Passo 1
Primeiro nó que conhecemos 2 das 3 correntes que passam por ele é:
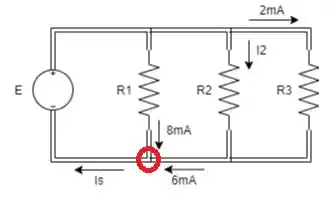
Pela LKC, a soma das correntes que entram no nó é igual a soma das correntes que saem do nó:
Passo 2
A corrente que entra na fonte de tensão é a mesma que sai da fonte de tensão, logo sabemos 2 das 3 correntes do seguinte nó:
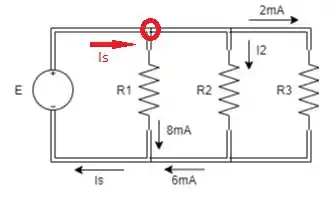
Percebemos que a corrente que desconhecemos deve estar saindo do nó:
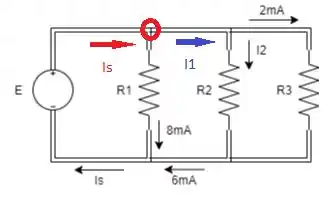
Passo 3
Pela LKC:
Passo 4
Para o nó:
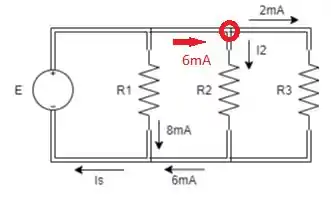
Aplicamos a LKC:
Resposta
Exercício Resolvido #9
Boylestad – 12 ed. – Capítulo 6 - Exercício 25
Usando a Lei de Kirchhoff para corrente, determine as correntes desconhecidas para as configurações complexas na figura:
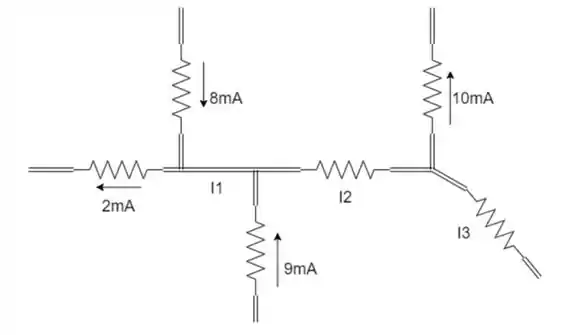
Passo 1
Através do nó:
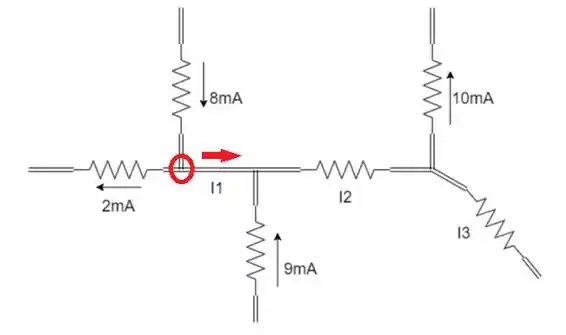
Utilizamos a LKC, ou seja, a soma das correntes que entram no nó é igual a soma das correntes que saem do nó:
Passo 2
Após conhecer , sabemos 2 das 3 correntes do seguinte nó:
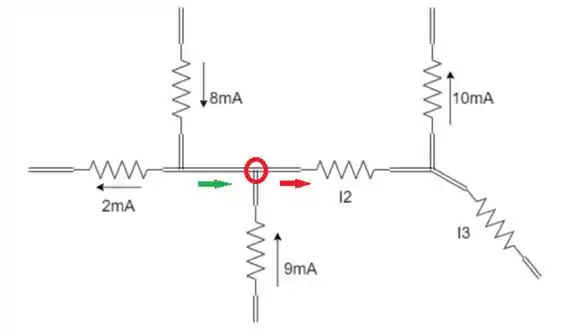
Pela LKC:
Passo 3
Após conhecer o valor de , sabemos 2 das 3 correntes do seguinte nó:
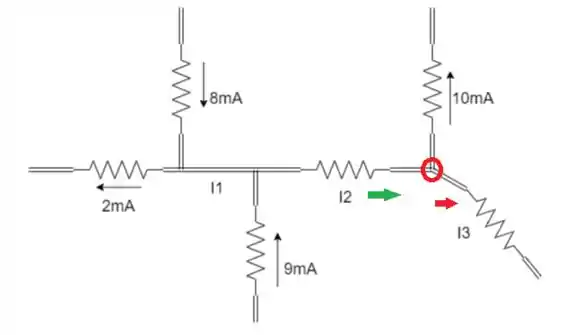
Pela LKC:
Resposta
Exercício Resolvido #10
Boylestad – 12 ed. – Capítulo 5 - Exercício 21 - Adaptada
Usando a Lei de Kirchhoff para tensões, descubra as tensões desconhecidas para o circuito:
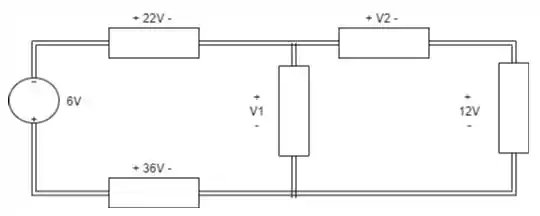
Passo 1
Analisando a primeira malha, podemos através da Lei de Kirchhoff para tensões descobrir o :
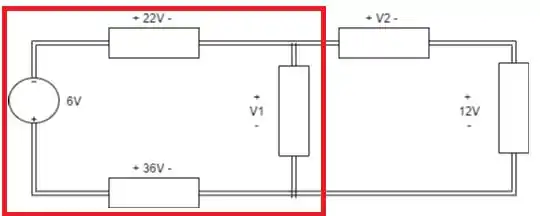
Assim, pela LKT, a soma das tensões em uma malha deve ser igual a zero. Devemos observar a polaridade das tensões!
Passo 2
Podemos analisar a segunda malha agora:
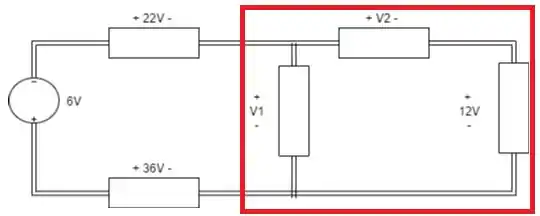
Já sabemos o valor de , assim pela LKT: