Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 73
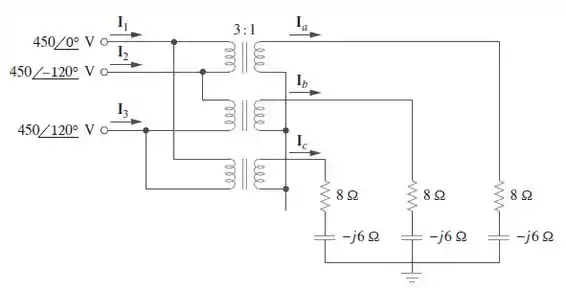
A figura ilustra um transformador trifásico que alimenta uma carga ligada em estrela.
- Identifique a conexão do transformador.
- Calcule as correntes e
- Determine a potência média absorvida média absorvida pela carga.
Passo 1
Galera, vamos lá pra letra (a). Observando o transformador que nos foi dado, podemos observar que o primário está ligado em delta, enquanto o secundário está ligado em estrela.
Passo 2
Para o lado primário, a tensão de linha do primário é igual a:
A tensão de linha secundária é igual a:
Como um sistema Y-Y, podemos usar um circuito equivalente por fase. Assim, no lado secundário:
E:
Desse modo, a corrente será igual a:
Nós podemos obter através da seguinte equação:
E por:
Dessa forma:
Passo 3
A potência média é aquela absorvida pela parte real da carga, ou seja, pelo resistor. Assim, a equação da potência é igual a:
Resposta
- A conexão é delta-estrela
- e
Exercícios de Livros Relacionados
42. Considere o circuito da figura 13.107 e determine a potência absorvida pelo resistor de 2Ω . Suponha que 80V seja um valor R M S .
41. Determine I 1 e I 2 no circuito abaixo.
43. Obtenha V 1 e V 2 no circuito do transformador ideal da Figura 13.108.
Um transformador ideal de 440 / 110V pode ser conectado para se tornar um autotransformador ideal de 550 / 440V . Existem quatro ligações possíveis, duas das quais estão erradas. Determine a tensão de
Na Fig. 16.2(a), N 2 = 500 espiras e ϕ 21 = 200 μ W b , quando i 1 = 2A . Determine v 2 se i 1 = 10 c o s 100 tA .