Encontre a solução da Equação de Laplace no retângulo , , que satisfaz as condições de contorno:
Passo 1
Vamos desenhar esse retângulo só para a gente entender melhor:
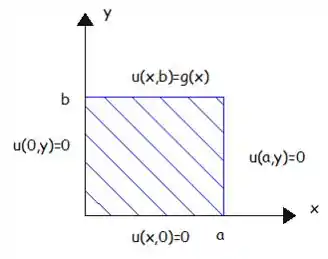
Essas são as condições que o problema dá.
Passo 2
Beleza, agora vamos fazer, como sempre, a separação de variáveis.
Procuramos uma solução do tipo . Como essa solução deve satisfazer a Equação de Laplace, temos:
Agora nós passamos tudo que tem para um lado e o que tem para o outro:
Como essa igualdade vale para todo e para todo , essas razões devem ser iguais a uma constante. Separando em duas equações, temos:
Aplicando a separação de variáveis para as condições homogêneas do problema (a função nós deixamos por último):
Então, temos o seguinte:
Passo 3
Resolver o problema que tem duas condições (de contorno)
Como a função é a que possui duas condições de contorno, vamos resolver primeiro o problema em , temos:
Temos a seguinte equação característica:
Vamos ver as soluções caso a caso agora.
Caso 1: . Ou seja, o que está dentro da raiz é positivo. Nesse caso, . As soluções são do tipo:
Agora vamos usar as condições de contorno:
Isso nos dá
Substituindo esses valores na nossa solução geral, temos
Mas isso não nos ajuda em nada! Essa é a solução trivial, que não nos interessa. Portanto, esse caso, , não nos dá soluções para a EDO.
Caso 2: . Nesse caso, . As soluções são do tipo:
Agora vamos usar as condições de contorno:
Isso nos dá
Substituindo esses valores na nossa solução geral, temos
Novamente, a solução trivial, que não nos ajuda em nada. Beleza, vamos ver o 3º caso agora!
Caso 3: . Ou seja, o que está dentro da raiz é negativo. Nesse caso, . As soluções são do tipo:
Substituindo
Agora vamos usar as condições de contorno:
Isso nos dá
Agora vamos com calma! Se tivermos , a solução é a trivial , que não nos interessa. Então, para essa igualdade ai em cima ser verdadeira, precisamos que o seno seja zero.
O seno se anula em , , ... , múltiplos inteiros de . Logo, podemos dizer que:
As soluções do 3º caso são então do tipo:
Passo 4
Tendo os valores de , resolver a outra EDO
Beleza, agora temos que resolver o problema em , temos:
A equação característica dessa EDO é a seguinte:
Já vimos que , não é? Quando encontramos seu valor no passo anterior. Então, as soluções dessa EDO são do tipo:
Não está errado escrever assim, mas é usual representar a solução dessa EDO (que é a combinação de exponenciais) dessa forma:
Então, as soluções da EDO em são:
Aplicando a condição :
Chegamos então a:
Então, podemos escrever o seguinte:
Passo 5
Escrever como série e achar os coeficientes da série
Como as combinações lineares de também são soluções do problema, temos que:
Agora vamos usar a condição que faltou:.
Repare que o coeficiente dos termos dessa série é tudo o que está no colchete! O que depende apenas de (não de ). Como essa é uma Série de Fourier de senos, fazendo uma extensão ímpar de , podemos dizer que:
Repare que o período da extensão é , não . Por isso apareceram esses ’s na integral, tome cuidado. O veio do denominador do seno.
Dessa forma, encontramos os coeficientes da série e substituímos em
Resposta
Onde