Série de Fourier

Fala aí galera bonita, sejam muito bem vindos ao Responde Aí, a plataforma de exatas criada para ajudar você a mandar super bem na sua prova!

Nossa missão aqui hoje é intriduzir a série de fourier. Partiu entender com o Responde Aí?

Série de Fourier

A série de fourier nada mais é que uma forma de representarmos funções como uma soma de senos e cossenos. Essa transformação de uma função em somas de senos e cossenos é muito útil quando temos aquelas funções super complexas, que dá até vontade de chorar hahahha. É muito melhor lidar com somas de senos e cossenos, que são funções que conhecemos, do que com uma função bizarra.

Beleza, mas aí você me pergunta: Como escrevo uma função na forma de série de fourier, ou seja, como transformo uma função em somas de senos e cossenos?

E eu te respondo. Não é um bicho de sete cabeças. A expressão da série de fourier é a seguinte:

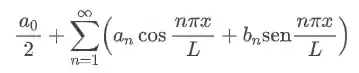
Agora vamos entender o que significa cada coisa que aparece aí na expressão.

Primeiro precisamos entender que nós temos o somatório de termos, e esse varia de até o , para que a série represente exatamente a função que queremos.

A variável aparece dentro do somatório, pois queremos representar uma função em forma de série, então a nossa variável independente tem que aparecer ali, beleza?

O é o período da função que queremos representar por série, ou seja, é o intervalo no qual a função se repete.

E , e são coeficientes da série de fourier, calculados da seguinte maneira:

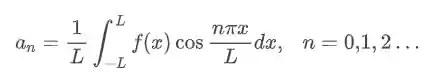
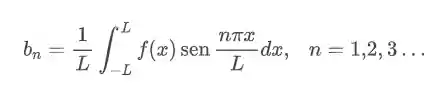
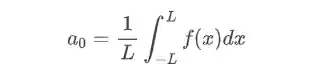
Só fica bem atento que na fórmula da série de fourier o aparece dividido por 2, beleza?

Eu sei que só esse bando de fórmula não diz muita coisa, não é? O bom mesmo é pegar um exercício e ver como que a gente aplica essas fórmulas para representarmos uma função por série de fourier. Para isso eu aconselho você a ver esse exercício aqui que mostra muito bem como fazemos isso passo a passo: Exercício - Série de Fourier.

Além de termos vários exercícios para você fixar o conteúdo em textos, nós temos também exercícios resolvidos passo a passo em vídeo. Para você conhecer um pouco como são os nossos vídeos e como solucionamos o problema passo a passo, eu vou deixar aqui embaixo um exercício resolvido em vídeo. Confere aí 👇🏽

Vídeo - Exercício

Confere esse exercício resolvido passo a passo em vídeo. Você vai adorar, pode confiar 😉

Curtiu essa introdução? Curtiu como o Responde Aí aborda o conteúdo de forma mais descontraída?

Se sim, você não sabe o que está perdendo. Nós temos todo o conteúdo que você precisa saber sobre série de fourier todo organizado e separado em capítulos e tópicos para que seu estudo seja bem focado e em uma ordem lógica. E o melhor de tudo, o conteúdo é passado para você de forma descontraída e muito didática. Está esperando o que para conferir o nosso Raio-X aqui embaixo e conhecer mais do Responde Ai e do nosso conteúdo? 👇🏽