]
(b)
integral arccos theta d thetaSolução: Fazemos a seguinte escolha:
u=arccos theta Rightarrow d u=-1raiz1-theta^2 d theta ; d v=d theta Rightarrow v=theta
Assim, utilizando
integral u d v=u v-integral v d u, escrevemos
integral arccos theta d theta=theta arccos theta+integral thetaraiz1-theta^2 d theta
Agora, para calcularmos esta última integral, fazemos a seguinte substituição:
t=raiz1-theta^2 Rightarrow d t=-thetaraiz1-theta^2 d theta
Então,
integral thetaraiz1-theta^2 d theta=-integral d t=-t+C=-raiz1-theta^2+C
Logo, subsituindo este resultado em (12), segue que
integral arccos theta d theta=theta arccos theta-raiz1-theta^2+C
©
integral x cossec^2 x d xSolução: Fazemos a seguinte escolha:
u=x Rightarrow d u=d x ; d v=cossec^2 x d x Rightarrow v=-cotg x
Assim, utilizando
integral u d v=u v-integral v d u, obtemos
integral x cossec^2 x d x=-x cotg x+integral cotg x d x
Note que a integral do segundo membro pode ser escrita como
integral cotg x d x=integral cos x d xsen x
Assim, fazendo
u=sen x Rightarrow d u=cos x d x, temos que
integral cotg x d x=integral cos x d xsen x=integral d uu=ln u+C=ln |sen x|+C
Logo, substituindo este resultado em (13), segue que
integral x cossec^2 x d x=-x cotg x+ln |sen x|+C
4.10 Determine o valor médio das seguintes funções ao longo do intervalo dado:
(a)
f(x)=-x^22 em
[0,2]Solução: Temos que
f med & =1b-a integrala^b f(x) d x & =12-0 integral0^2-x^22 d x & =(-x^312)|0 ^2 & =-2^312+0 & =-23
Logo,
f med =-23 é o valor médio de
f no intervalo dado.
(b)
g(t)=t^2-t em
[-1,2]Solução: Temos que
g med & =1b-a integrala^b g(t) d t & =12-(-1) integral-1^2(t^2-t) d t & =13(t^33-t^22)|-1 ^2 & =13[(2^33-2^22)-((-1)^33-(-1)^22)] & =12
Logo,
g med =12 é o valor médio de
g no intervalo dado.
4. 11 Com
t meses de experiência um funcionário do correio é capaz de separar
Q(t)=
700-400 e^-0,5 t cartas por hora. Qual a velocidade média com que o funcionário consegue separar a correspondência durante os 5 primeiros meses de trabalho?
Dica: Use o TVM para integrais.
Solução: Utilizando o TVM para integrais e considerando a função
Q(t) no intervalo
[0,5], temos que a velocidade média será dada por
Q(t)med & =15-0 integral0^5(700-400 e^-0,5 t) d t & =15[(700 t)|0 ^5-400 integral0^5 e^-0,5 t d t] & =15[700 cdot 5-400 integral0^5 e^-0,5 t d t] & =700-80 integral0^5 e^-0,5 t d t
Podemos calcular esta última integral fazendo a substituição
u=-0,5 t Rightarrow d u=-0,5 d t, x=0 Rightarrow u=0, x=5 Rightarrow u=-2,5
Então,
Q(t) med & =700-80 integral0^-2,5 e^u d u-0,5 & =700+160 integral0^-2,5 e^u d u & =700+160(e^u)|0 ^-2,5 & =700+160(e^-2,5-1) & approx 553,13
Logo, a velocidade média é aproximadamente 553,13 cartas por hora.
4. 12 Calcule as seguintes integrais:
(a)
integral ln ^3 x d xSolução: Podemos utilizar integração por partes
u=ln ^3 x, d u=3 ln ^2 xx, d v=d x, v=x escolhendo
integral ln ^3 x d x & =x ln ^3 x-3 integral x ln ^2 xx d x & =x ln ^3 x-3 integral ln ^2 x d x
Então,
u=ln ^2 x, d u=2 ln xx, d v=d x, v=x
Esta última integral também pode ser resolvida por partes. Para isso, escolhemos
integral ln ^2 x d x & =x ln ^2 x-2 integral x ln xx d x & =x ln ^2 x-2 integral ln x d x
Então,
u=ln x, d u=1x, d v=d x, v=x
Finalmente, para esta última integral, escolhemos
integral ln x d x & =x ln x-integral x 1x d x & =x ln x-x+C
Então,
integral ln ^3 x d x & =x ln ^3 x-3 integral ln ^2 x d x & =x ln ^3 x-3(x ln ^2 x-2 integral ln x d x) & =x ln ^3 x-3(x ln ^2 x-2(x ln x-x))+C
Logo, substituindo (16) e (15) em (14), segue que
Solução: Podemos utilizar a regra da substituição. Assim, escolhendo
d u=3 d x
integral x(2+3 x)^13 d x & =integral(u-23) u^13 d u3 & =19 integral(u^43-2 u^13) d u & =19(3 u^737-2 cdot 3 u^434)+C , temos que
integral x(2+3 x)^13 d x=19(3(2+3 x)^737-3(2+3 x)^432)+C
Logo, voltando para a variável original, segue que
©
sen^2 x=1-cos (2 x)2 e cos ^2 x=1+cos (2 x)2 Solução: Utilizando as identidades
integral sen^4 x d x & =integral(sen^2 x)^2 d x & =integral (1-cos (2 x))^24 d x & =14 integral(1-2 cos (2 x)+cos ^2(2 x)) d x & =14 integral d x-12 integral cos (2 x) d x+14 integral cos ^2(2 x) d x & =x4-12 integral cos (2 x) d x+14 integral 1+cos (4 x)2 d x & =x4-12 integral cos (2 x) d x+18 integral d x+18 integral cos (4 x) d x & =3 x8-12 integral cos (2 x) d x+18 integral cos (4 x) d x
podemos escrever
integral cos (2 x) d x=sen(2 x)2+C1 e integral cos (4 x) d x=sen(4 x)4+C2
Note que, utilizando uma substituição simples, podemos calcular facilmente estas duas últimas integrais e obter
integral sen^4 x d x & =3 x8-12(sen(2 x)2)+18(sen(4 x)4)+C & =3 x8-sen(2 x)4+sen(4 x)32+C
Logo,
onde
u=u(x).
4. 13 Verdadeiro ou Falso. Se for verdadeiro, explique. Se for falso, explique ou dê um contraexemplo.
(a) A fórmula da integração por partes é obtida pela regra do produto para derivadas.
Solução: Verdadeiro! Da regra de derivação de um produto de duas funções
v=v(x) e
(u v)^prime=u^prime v+u v^prime ,
u(x) v(x)=integral u^prime(x) v(x) d x+integral u(x) v(x) d x
segue por integração,
integral u v^prime d x=u v-integral u^prime v d x
ou ainda,
integral u d v=u v-integral v d u
que pode ser escrita na forma
(b) Toda função integrável é contínua.
Solução: Falso! Como contra-exemplo, considere a função
x=0 que é integrável de 0 a 1 , mas não é definida em
c in[a, b].
© O Teorema do Valor Médio para integrais garante que existe um único ponto
f(c)(b-a)=integrala^b f(x) d x tal que
Solução: Verdadeiro! O TVM garante que existe um
f(c)=fmed=1b-a integrala^b f(x) d x tal que
Geometricamente, indica que existe um ponto no qual ao traçarmos uma reta horizontal na imagem de
f, a área acima da reta e limitada por
x é igual a área abaixo da reta até o eixo
integral-3^3 raiz9-x^2 d x.
4. 14 Esboce o gráfico dos integrandos e use áreas para calcular as integrais.
(a)
f(x)=raiz9-x^2Solução: Note que o gráfico da função
Área =pi r^22=pi cdot 3^22=9 pi2 ua corresponde ao semicírculo de raio igual a 3 , conforme indica a figura abaixo:
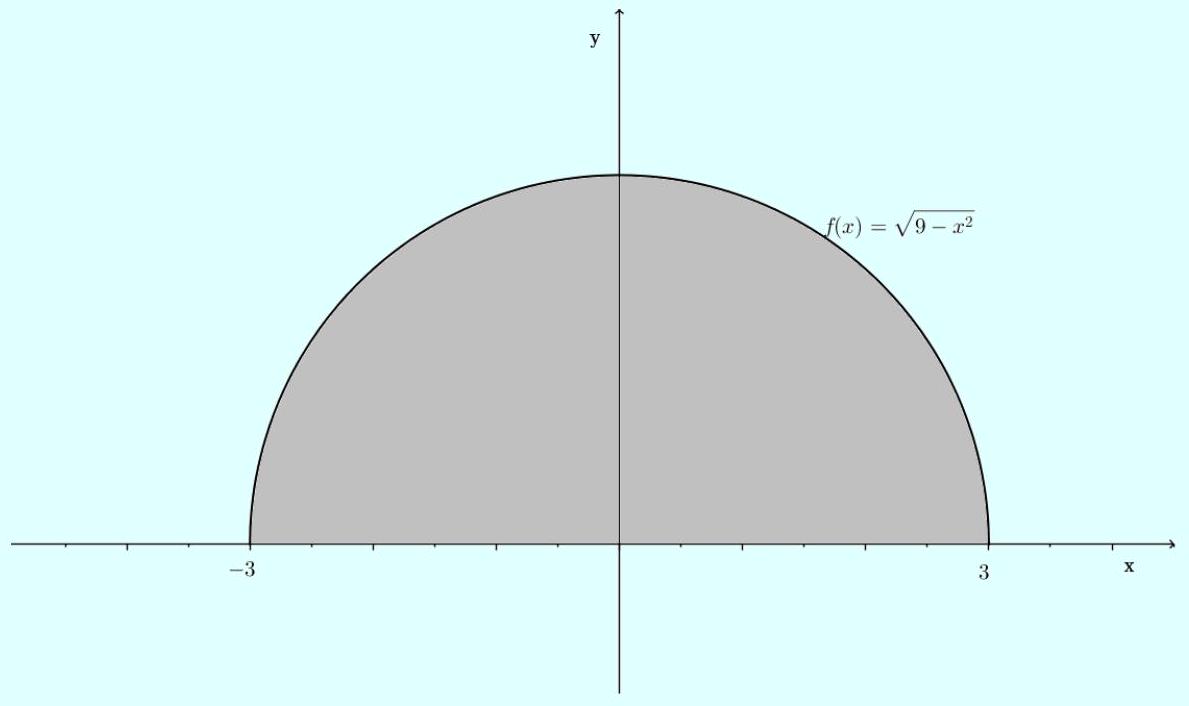
Logo, a área descrita pela integral é dada por
Solução: Observe que a região limitada pelo gráfico da função
x=-1, x=2, pelas retas
y=0 e
Área =A1+A2=(2+1) cdot 12+2 cdot 22=72 ua é da seguinte forma
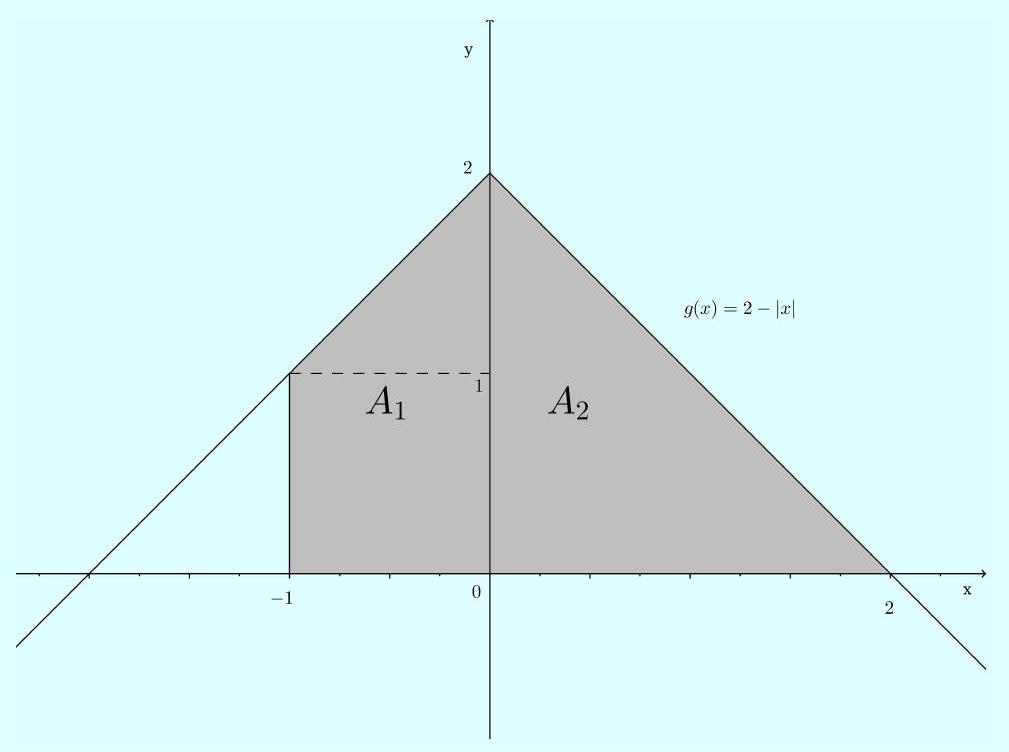
Logo, a área descrita pela integral é dada por
Solução: Observe que a região limitada pelo gráfico da função
y=0, pelas retas
Área =A1+A2=pi cdot 2^22+4 cdot 1=2 pi+4 approx 10,283 ua e
integral0^2 pi sen x d x é da seguinte forma
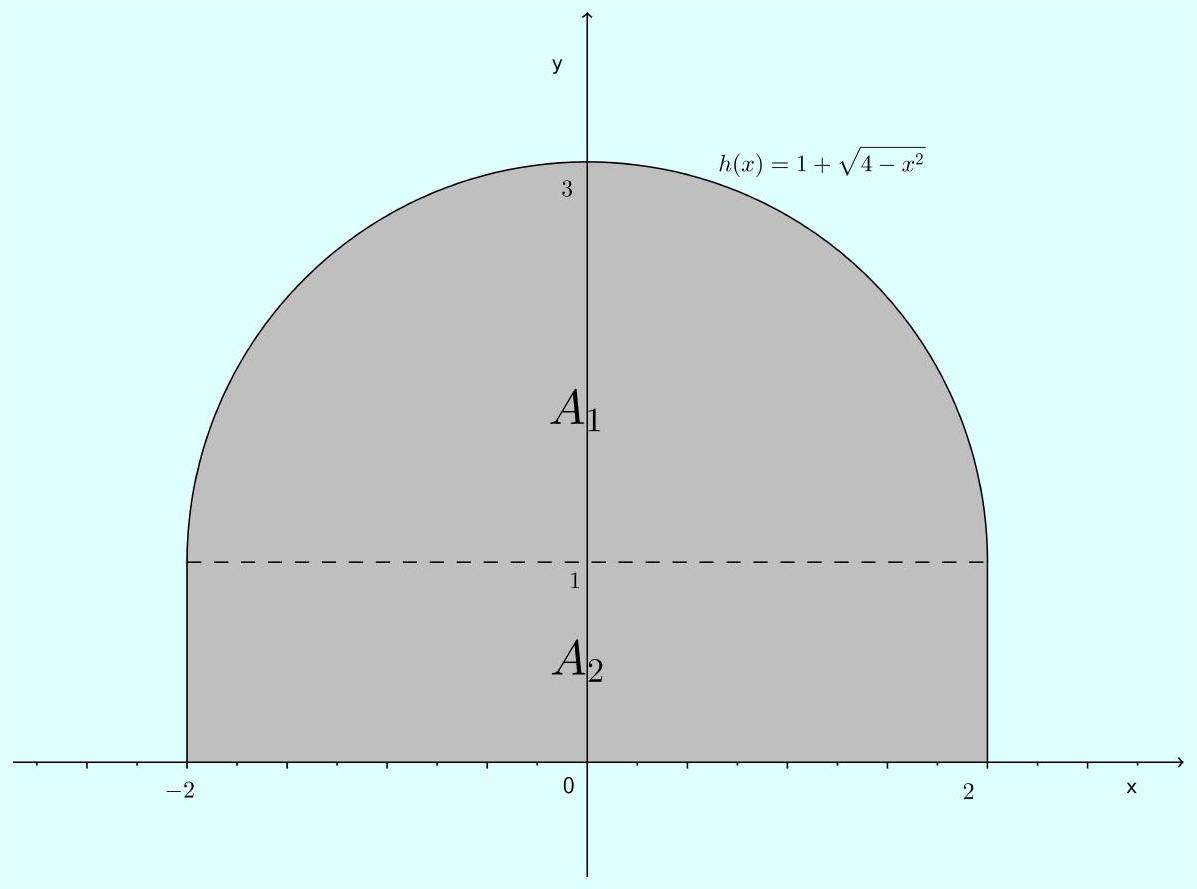
Logo, a área descrita pela integral é dada por
integral0^2 pi sen x d x=(-cos x)|0 ^2 pi=-1+1=0 Á
(a) Qual o valor da integral
f(x)=sen x ?
Solução: Temos que
(b) Sabendo do resultado do item (a), é verdade que podemos entender a integral acima como sendo a área compreendida entre o gráfico da função
x=0, o eixo
x=2 pi e as retas
A1 e
A2 ? Explique.
Solução: Não é verdade, pois a região possui área, como podemos ver no gráfico abaixo:
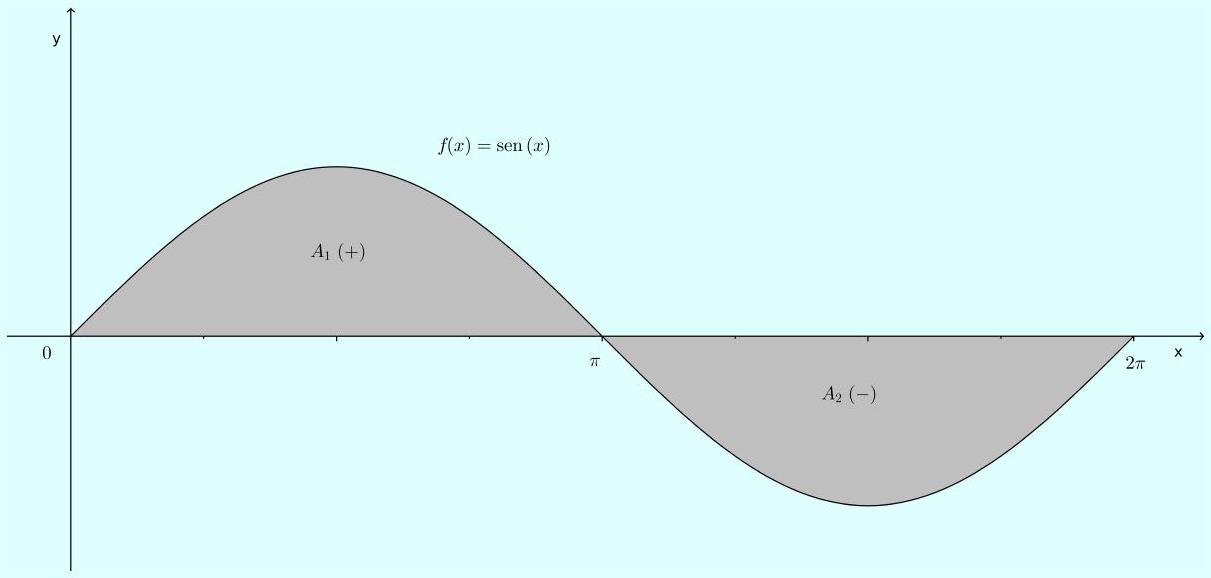
Note que as áreas
A1=integral0^pi sen x d x=2 e
A2=integralpi^2 pi sen x d x=-2 podem ser calculadas da seguinte forma:
e
Assim,
integral0^2 pi sen x d x & =integral0^pi sen x d x-integralpi^2 pi sen x d x & =(-cos x)|0 ^pi+(cos x)|pi ^2 pi & =(-1(-1)-(-1))+(1-(-1)) & =4
© Elabore uma maneira para calcular a área da região descrita no item (b).
Solução: Para calcularmos a área da região descrita no ítem (b), separamos a integral em duas partes considerando o sinal de
9 % em cada intervalo. Assim,
Logo, 4 u.a. é a área da região dada.
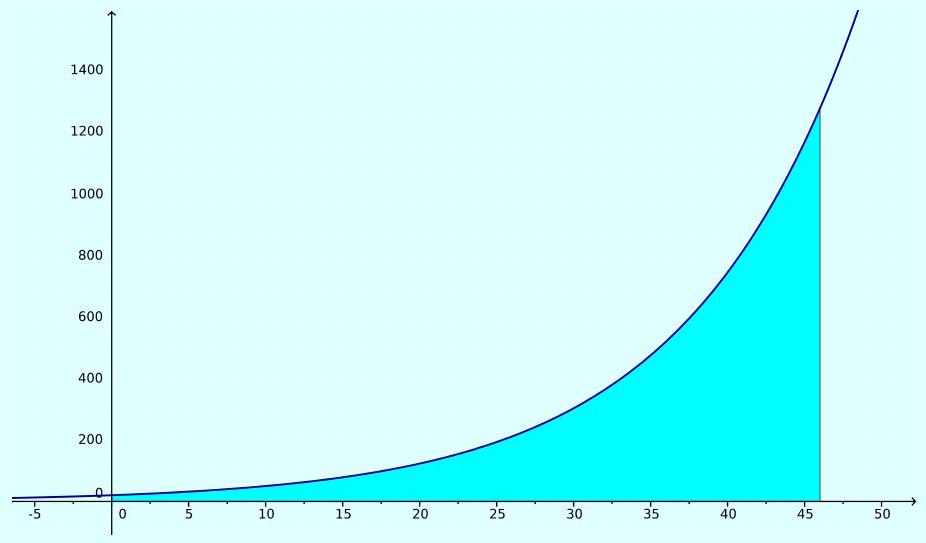
4. 16 Se em 1970, foram utilizados 20,3 bilhões de barris de petróleo no mundo todo e se a demanda mundial de petróleo cresce exponencialmente a uma taxa de
t ao ano, então a demanda
A(t)=20,3 e^0,09 t(t=0 em 1970) anual de petróleo no tempo
9 % é
2016 ?. Se a demanda continua crescendo a uma taxa de
t=0 ao ano, qual será a quantidade de petróleo
consumida entre os anos de 1970 e
t=46
Solução: A quantidade de petróleo utilizada nesse período de tempo é a área sob a curva de demanda entre
20,3 integral0^46 e^0,09 t d t=225,56 e^0,09 t|0 ^46 approx 13940 e
y=-2 x3, y=x-5.
Então,
Logo, foram consumidos aproximadamente 13940 barris de petróleo.
4. 17 Calcule as áreas das figuras determinadas pelas curvas dadas:
(a)
-2 x3=x-5 e
x=3.
Solução: Temos que:
Note que as retas se interceptam quando
A=integral0^3[-2 x3-(x-5)] d x=[-x^23-x^22+5 x]0^3=-93-92+15=7,5 ua
isto é, quando
y=x^2. Logo, a área procurada é
(b)
x^2=raizx Rightarrow x=0 e
x=1.
Solução: Temos que:
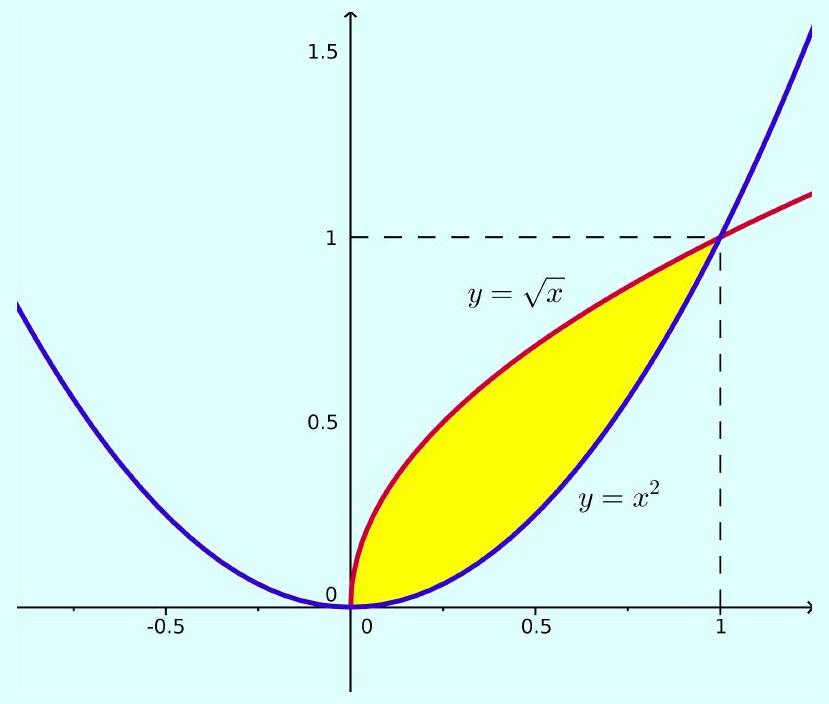
Note que as curvas se interceptam quando
A=integral0^1(raizx-x^2) d x=(2 x^32-x^33)|0 ^1=13 ua e
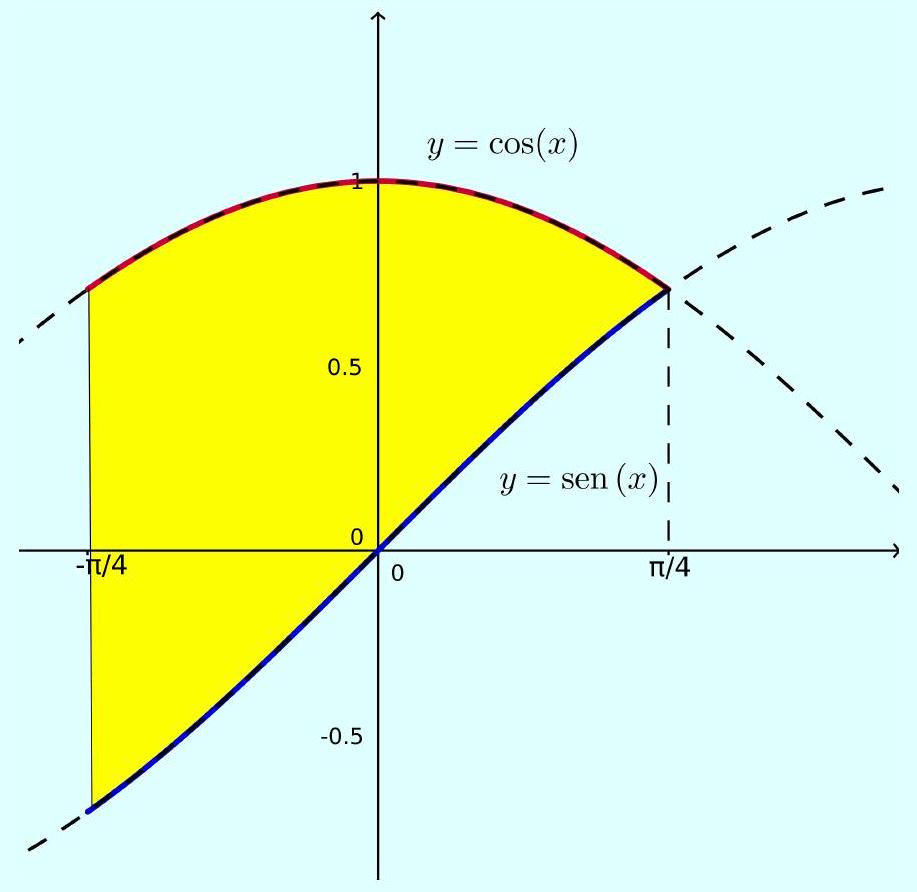
y=cos x, y=sen x, x=-pi4.
Logo,
©
A=integral-pi / 4^pi / 4(cos x-sen x) d x=raiz2 ua e
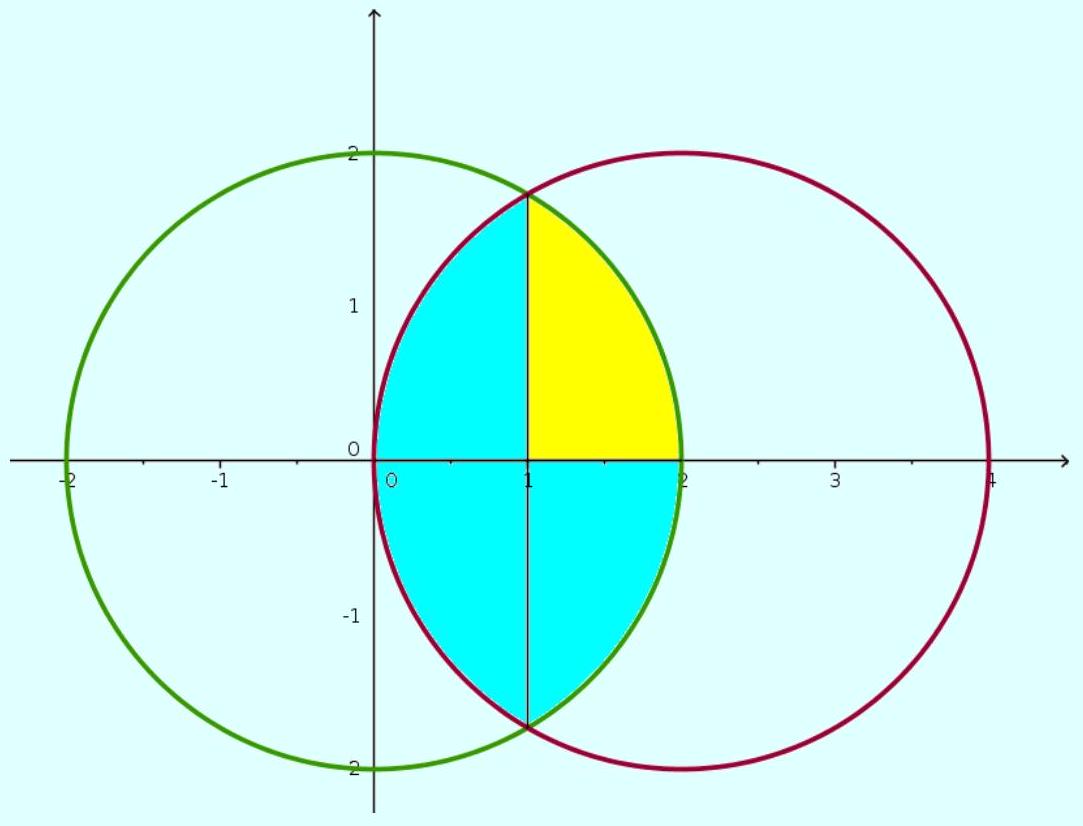
x^2+y^2 <= 4 x.
Solução: Temos que:
Logo, a área será
(d) A área comum a
x^2+y^2=4 x Rightarrow(x-2)^2+y^2=4 e
(2,0).
Solução: Note que, completando quadrados, temos que a equação:
corresponde a um círculo de raio 2 com centro em
l x^2+y^2=4 x^2+y^2=4 x . E que
x=1 corresponde a um círculo com raio 2 e centrado na origem.
Determinamos o intervalo de integração, resolvendo o sistema:
Então,
(x, y) mid 0 <= y <= raiz3, 1 <= x <= raiz4-x^2 e
y. Pela simetria da região, calculamos somente a área da região:
A & =4 integral0^raiz3(raiz4-y^2-1) d y & =4(integral0^raiz3 raiz4-y^2 d y-integral0^raiz3 d y) & =4(integral0^raiz3 raiz4-y^2 d y-raiz3)
no primeiro quadrante (em amarelo) e multiplicamos por quatro. Integrando em relação a
integral0^raiz3 raiz4-y^2 d y :
y=2 sen theta Rightarrow d u=2 cos theta d theta
Agora, calculemos
y=0 Rightarrow theta=0 fazendo
y=raiz3 Rightarrow theta=pi3. Observe que
integral0^raiz3 raiz4-y^2 d y & =4 integral0^pi / 3 cos ^2 theta d theta & =2 pi3+raiz32 e
A=4(integral0^raiz3 raiz4-y^2 d y-raiz3)=8 pi3-2 raiz3 ua . Então,
Substituindo este resultado em (17), segue que:
t=x^2 Rightarrow d t=2 x d x ou d t2=x d x
- 18 Calcule as seguintes integrais:
(a)
integral x^3 e^x^2 d x=12 integral t e^t d t .
Solução: Primeiramente, fazemos
u=t Rightarrow d u=d t, d v=d t Rightarrow v=e^t
Então,
integral x^3 e^x^2 d x=12 integral t e^t d t=12(t e^t-integral e^t d t)=12(t e^t-e^t)+C
Integrando por partes, fazemos
integral x^3 e^x^2 d x=12(x^2 e^x^2-e^x^2)+C
Então,
Logo, voltando para a variável original, segue que