Analogia entre a transferência de massa e de movimento

Esse enunciado tá pedindo pra gente a analogia padrão entre os fenômenos de transferência de massa e de quantidade de movimento, ok?

Vamos nessa então! Analisando as magnitudes dos fluxos na fronteira e sendo a espessura da camada limite turbulenta dinâmica e , a espessura da camada limite turbulenta mássica, vamos ter:

e

Dividindo essas equações, uma pela outra vamos ficar com:

Sendo o número de Schmidt turbulento dado por:

E considerando que:

e

A equação ficará:

Arrumando ela ficaremos com:

E lembrando que o coeficiente de atrito, pode ser dado por:

E correlacionando o com o coeficiente de atrito, podemos considerar que:

Substituindo isso na equação que temos:

E recordando que o número de Stanton mássico é definido por:

A equação ficará com essa cara aqui:

Comparando isso com o número de Stanton mássico, é como se a gente tivesse:

Isso mostra pra gente que:

O coeficiente de transferência de massa é proporcional ao coeficiente de atrito, mostrando assim a analogia entre a transferência de massa e a quantidade de movimento.

Fala aí!! Tudo ok? O enunciado tá pedindo pra gente o objetivo de ter as analogias de Reynolds, Prandtl, Von Kármán e Chilton-Colburn e quais as condições que elas devem ser aplicadas.

Bom, o objetivo dessas analogias é simplificar a obtenção do fator ,que será diferente para cada situação que será abordada, ou seja essas analogias se fazem necessárias para identificar qual será a contribuição de nas diferentes zonas de escoamento… Dá uma olhadinha nessa figura abaixo, que representa o escoamento em uma placa plana:

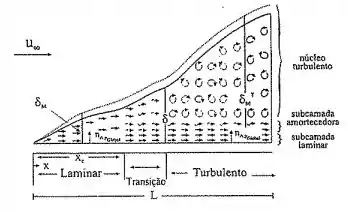
Vamos ter zonas de escoamento diferentes, mesmo analisando só a parte da turbulência…

Olha só, a analogia de Reynolds vai considerar que todo o escoamento é uma coisa só, e vai funcionar como uma única camada turbulenta, já a analogia de Prandtl considera uma parte laminar e a outra turbulenta, a analogia de Von Kármán vai considerar a parte laminar, a turbulenta e a zona de amortecedora, que será a transição entre elas, e a analogia de Chilton-Colburn, considera a existência apenas de um núcleo turbulento.

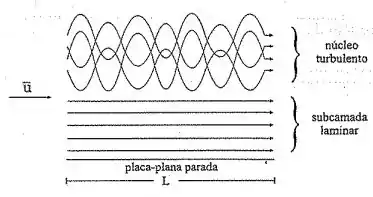
Bom, a analogia desses dois caras é bem semelhante, principalmente porque o Von Kármán se baseou no desenvolvimento de Prandtl. A principal diferença é que Prandtl dividiu seu escoamento em duas zonas, uma subcamada laminar e um núcleo turbulento, desse jeitinho da imagem:

Já o Von Kármán, buscando aperfeiçoar esse modelo incluiu uma subcamada de transição entre essas duas zonas, que chamou de subcamada amortecedora, dá só uma olhadinha:

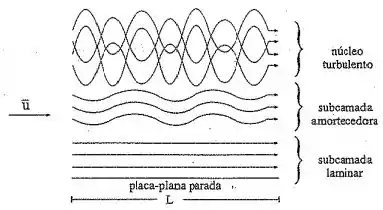
A presença dessa subcamada torna o modelo mais próximo da realidade e é por conta dela que temos o aparecimento do logaritmo na equação do fator , deixando a equação dele desse jeito:

Se a gente tira essa parte do logaritmo, temos exatamente o fator , para a analogia de Prandtl, olha só:

Show de bolinhas!

Olha que continha linda pra gente fazer!! O enunciado quer que a gente use a analogia de Chilton-Colburn… Ela é aquela que se baseia em Reynolds, mas considera um núcleo turbulento, beleza? Vamos lá!

Estamos trabalhando com um tubo de naftaleno, logo um tubo liso, podemos encontrar o coeficiente médio de atrito com a seguinte relação:

Opa! Então precisamos do número de Reynolds antes:

Substituindo os dados, temos:

Olha que legal! Isso confirma que estamos em regime turbulento e podemos usar essa analogia mesmo haha

Voltando lá no coeficiente de atrito, ficaremos com:

E lembrando á da teoria quando dizemos que:

Vamos ter:

E se:

Nós podemos dizer que:

Rearranjando, vamos ficar com:

E sendo:

Teremos então que o nosso coeficiente convectivo de massa, nessa situação, ficará:

Substituindo o que foi dado no enunciado:

Prontinho!!!

Fala aí! Esse enunciado quer algo bem parecido com o anterior, né? A diferença é que agora estamos em uma tubulação retangular, certo? Então vamos nessa!

Estamos trabalhando com um tubo retangular, então precisamos encontrar o diâmetro hidráulico dele:

Como ele deu pra gente o e o , vamos ficar com:

Beleza! A parte nova pra gente já foi! Agora é o que já tínhamos visto antes!

Precisamos do número de Reynolds:

Que será:

Estamos em regime turbulento! Só pra confirmar haha

Achando o coeficiente de atrito:

Logo, o fator de Chilton-Colburn, é:

Podemos encontrar o coeficiente convectivo de massa, usando a relação:

Substituindo o que foi dado no enunciado:

Arrasamos!

Vamos para mais uma questãozinha! Precisamos encontrar o número de Stanton mássico através da analogia de Prandtl, sendo dado pra gente o número de Schmidt e o coeficiente de atrito… humm… Bom, precisamos lembrar dessa relação aqui:

E segundo Prandtl, temos que:

Como estamos trabalhando com uma placa plana nossa constante será:

Teremos então:

Opa! Mais ainda falta esse cara aqui , podemos encontrar ele com a relação:

Voltando para a analogia de Prandtl:

Por fim, vamos encontrar o número de Stanton:

É isso aí!

Vamos nessa! Precisamos encontrar o coeficiente convectivo usando a analogia de Von Kármán, precisamos lembrar dessa relação aqui:

E segundo Von Kármán, temos que:

Como estamos trabalhando com um tubo liso nossa constante será:

Opa! Agora só falta o , podemos usar a relação:

Voltando para a analogia de Von Kármán:

Agora sim podemos encontrar nosso coeficiente convectivo:

Pronto! Conseguimos!

Estamos trabalhando com um reservatório retangular e vamos considerar que estamos com um tubo liso… Isso é para que a gente possa usar a analogia de Chilton-Colburn!

Vamos começar encontrando o coeficiente médio de atrito:

Precisamos do número de Reynolds, mas antes disso vamos encontrar o diâmetro hidráulico do reservatório:

Como temos e , vamos encontrar o diâmetro como sendo:

Agora voltando ao Reynolds, vamos ter:

Voltando lá no coeficiente de atrito, ficaremos com:

Então temos que:

E sendo:

Nós podemos dizer que:

Ficaremos então:

Opa! Tá faltando encontrar o número de Schmidt:

Teremos então que o nosso coeficiente convectivo de massa, será:

Show de bola!