Método da Média Logarítmica
Teoria
Introdução
Tá... talvez o nome não seja dos mais bonitos, mas esse é um cara realmente importante pra nós, porque ele vai nos ajudar a calcular a taxa de transferência de calor em um trocador de maneira mais adequada.
Até então, quando tínhamos que calcular a taxa de transferência de calor, podíamos utilizar essas equações:
Onde os índices e são referentes aos fluidos quente e frio, respectivamente.
Essas equações partem do princípio que os fluidos trocam calor somente entre si, e que qualquer influência das vizinhanças pode ser desconsiderada.
Agora, para calcular a taxa de transferência de calor a partir do coeficiente global de transferência de calor , temos que usar uma diferença de temperatura adequada .
Onde é a diferença de temperatura média logarítmica, dado por:
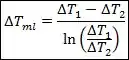
Os índices “1” e “2” correspondem às extremidades do trocador. Na hora de calcular esse cara, não faz diferença qual extremidade você escolhe como “1” e qual você escolhe como “2”, isso não altera o valor de .
“Não podemos fazer simplesmente uma média das diferenças de temperatura?!”
Não, não podemos fazer isso porque a diferença de temperatura entre os fluidos quente e frio varia ao longo do trocador de calor. Assim, usar a diferença de temperatura média logarítmica é a forma mais adequada pra calcularmos a taxa de transferência de calor.
Vamos pensar na seguinte situação:
Temos um trocador de calor de escoamento paralelo, com de diâmetro e de comprimento, onde água entra a e sai a com vazão mássica de , enquanto gases quentes em escoamento anular entram no trocador a e o deixam a .
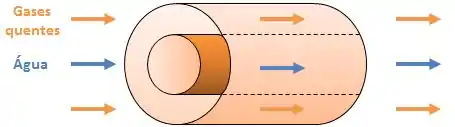
O que queremos saber aqui é: qual é o coeficiente global de transferência de calor do trocador?
Pra isso, precisamos saber como tratar da diferença de temperatura média logarítmica para diferentes trocadores, começando justamente pelo caso que estamos trabalhando.
Trocador de Calor de Escoamento Paralelo
Nesse tipo de trocador, como temos os fluidos quente e frio entrando no trocador no mesmo ponto.
Assim que eles entram (fluido quente a temperatura máxima e fluido frio a temperatura mínima), a diferença entre as suas temperaturas é máxima, e vai decaindo ao longo do trocador.
Graficamente, a temperatura dos fluidos varia dessa forma:
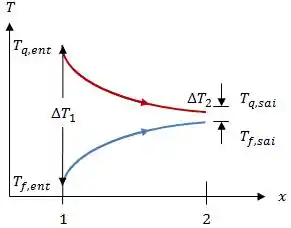
Assim, para trocadores de calor de escoamento paralelo, as diferenças de temperatura serão:
Logo, para o nosso problema:
Daqui, já podemos até resolver o nosso problema, uma vez que a taxa de transferência de calor pode ser dada por:
Finalmente, o coeficiente global de transferência de calor será dado por>
Substituindo os valores:
Show de bola! Resolvemos o nosso problema, agora temos que saber como proceder se o trocador de calor for diferente.
Trocador de Calor de Escoamento Contracorrente
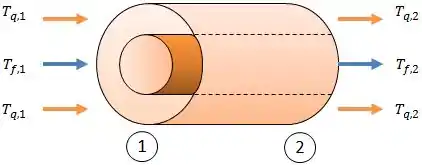
Diferente do trocador de calor de escoamento paralelo, neste caso os fluidos quente e frio entram por extremidades opostas, como mostra a figura.
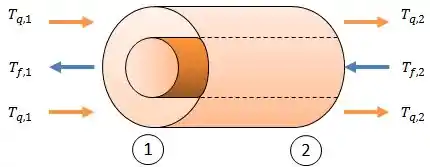
Dessa forma, esse trocador proporciona a transferência de calor entre as porções mais quentes dos dois fluidos em uma extremidade, bem como entre as porções mais frias dos dois fluidos na outra extremidade.
Graficamente, a temperatura nos dois fluidos varia da seguinte forma:
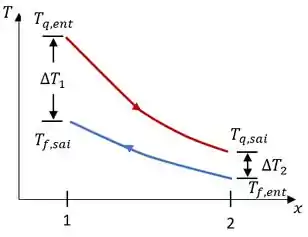
Na prática, a diferença é que as diferenças de temperaturas e serão dadas por:
E se tivermos outros tipos de Trocadores de Calor?!
Nesse caso, a gente pode simplesmente multiplicar a diferença de temperatura média logarítmica por um fator de correção, também chamado de fator de forma , da seguinte forma:
Onde é a diferença de temperatura média logarítmica para o caso de um trocador de calor contracorrente, então vamos ter que calcular esse cara considerando as diferenças de temperatura que acabamos de ver, ou seja:
O fator de correção é basicamente utilizado para o trocador de calor casco e tubo e o trocador de calor de escoamento cruzado.
“Show de bola! Mas como eu calculo esse cara?!”
Bem, a gente vai pegar o seu valor através de gráficos, se liga:
- Trocador de casco e tubo:
- Trocador de calor de escoamento cruzado:
Para o caso de 2, 4, 6, ... (qualquer múltiplo de 2) passes nos tubos:
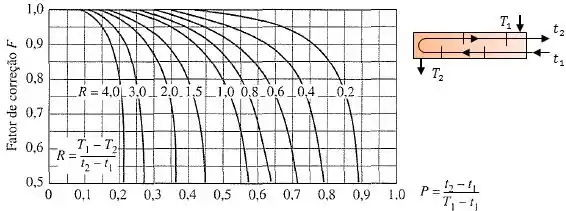
Para o caso de 4, 8, 12, ... (qualquer múltiplo de 4) passes no tubos:
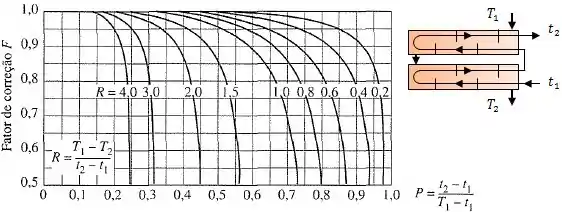
Para o caso de um único passe e com os dois fluidos sem mistura.
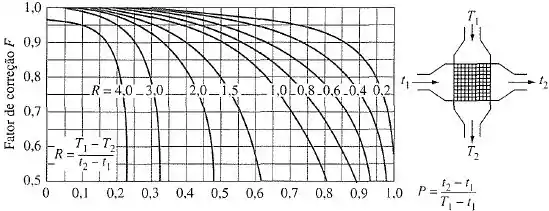
No caso de um único passe, com um fluido com mistura e outro fluido sem mistura:
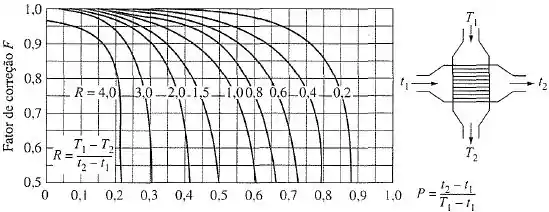
Para encontrar o valor correspondente nos gráficos, temos que calcular as seguintes grandezas:
Só fique esperto que no trocador de calor de casco e tubo, representa a temperatura no casco e representa a temperatura no tubo.
Obs.: Nos casos em que há mudança de estado físico no trocador, como não há variação de temperatura , o termo será nulo e o fator de correção será .
Vamos colocar isso tudo em prática? Responde Aí!
Trocador de Calor de Escoamento Paralelo
Trocador de Calor de Escoamento Contracorrente
E se tivermos outros tipos de Trocadores de Calor?!
Exercícios Resolvidos
Exercício Resolvido #1
ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.
Um trocador de calor de tubo duplo de escoamento paralelo é utilizado para aquecer água fria com água quente. A água quente entra no tubo a com uma taxa de e deixa-o a .
O trocador de calor não é bem isolado e estima-se que do calor fornecido pelo fluido quente é perdido no trocador de calor.
Se o coeficiente global de transferência de calor e a superfície do trocador de calor são e , respectivamente, determinar a taxa de transferência de calor para a água fria e a diferença de temperatura média logarítmica para este trocador de calor.
Passo 1
Vamos começar pela taxa de transferência de calor para a água fria.
A taxa de transferência de calor que sai da água quente é dada por:
Como já temos os dados da água quente, basta substituir os valores, onde:
Logo:
No entanto, 3% do calor fornecido pelo fluido quente é perdido no trocador de calor, de forma que somente 97% é transferido para a água fria. Logo:
Passo 2
Agora que temos a taxa de transferência de calor que é efetivamente trocada entre os fluidos, podemos encontrar a diferença de temperatura média logarítmica através da seguinte expressão:
Onde:
Logo:
Resposta
Exercício Resolvido #2
ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.
Um trocador de calor de tubo duplo em contracorrente resfria etileno glicol escoando com uma taxa de de a com água que entra a e deixa-o a .
O coeficiente global de transferência de calor com base na superfície interna do tubo é de .
Determinar a taxa de transferência de calor, a vazão mássica da água e a superfície de transferência de calor na face interna do tubo.
Passo 1
Determinar a taxa de transferência de calor.
Podemos calcular a taxa de transferência de calor utilizando tanto os dados do fluido frio, quanto os do fluido quente:
Como temos a vazão mássica do etileno glicol, vamos usar a equação para o fluido quente, onde:
Logo:
Passo 2
Determinar a vazão mássica da água.
Agora que já temos a taxa de transferência de calor, podemos calcular a vazão mássica da água através da seguinte equação:
Onde:
Logo:
Passo 3
Determinar a superfície de transferência de calor na face interna do tubo.
Ok, como queremos determinar a área de transferência de calor, a fórmula mais adequada é essa:
Como já temos o coeficiente global de transferência de calor , vamos precisar da diferença de temperatura média logarítmica, dada por:
Já que estamos trabalhando com um trocador de calor de escoamento contra corrente, as diferenças de temperaturas e serão:
Logo:
Dessa forma, a área superficial será:
Resposta
Exercício Resolvido #3
ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.
O vapor no condensador de vapor de uma central elétrica deve ser condensado a uma temperatura de com água de refrigeração de um lago nas proximidades, que entra nos tubos do condensador a e deixa-os a .
A superfície dos tubos é de e o coeficiente global de transferência de calor é de .
Determinar a vazão mássica necessária para água de resfriamento e a taxa de condensação do vapor no condensador.
Passo 1
Vamos nessa! A vazão mássica da água de resfriamento (fluido frio) pode ser calculada da seguinte forma:
Já a taxa de condensação do vapor no condensador (fluido quente) é dada por:
De qualquer forma, vamos precisar da taxa de transferência de calor.
Passo 2
Para isso, podemos usar a seguinte equação:
O problema nos deu o coeficiente global de transferência de calor e a área de troca térmica .
A diferença de temperatura média logarítmica é calculada considerando o caso de escoamento contracorrente, logo:
Logo:
Obs.: Como há mudança defase em um dos fluidos, o fator de correção será . Então não precisamos nos preocupar com ele nesses casos.
Dessa forma, a taxa de transferência de calor será:
Passo 3
Voltando aos caras que precisamos calcular, a vazão mássica da água de resfriamento será:
Passo 4
Por fim, a taxa de condensação do vapor no condensador será:
Onde , logo:
Resposta
Exercício Resolvido #4
ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.
Um trocador de calor casco e tubo com 2 passes no casco e 8 passes no tubo é utilizado para aquecer álcool etílico nos tubos de a com uma taxa de .
O aquecimento deve ser feito pela água que entra no lado do casco a e deixa-o a .
Se o coeficiente global de transferência de calor é de , determine a superfície de transferência de calor do trocador de calor.
Passo 1
Podemos calcular a área superficial de transferência de calor através da seguinte equação:
Daqui, não temos nem a taxa de transferência de calor , e nem a diferença de temperatura média logarítmica .
Então vamos atrás deles.
Passo 2
Como temos a vazão mássica de álcool etílico (fluido frio), a taxa de transferência de calor pode ser calculada através da seguinte equação:
Substituindo os valores, teremos:
Passo 3
Como temos um trocador de calor casco e tubo, a diferença de temperatura média logarítmica será dada por:
Onde:
Logo:
Para o fator de correção, teremos:
Levando em consideração que temos 2 passes de casco e 8 passes nos tubos, de acordo com o gráfico abaixo:
Finalmente:
Passo 4
Finalmente, a área superficial será:
Onde . Logo:
Resposta
Exercício Resolvido #5
ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.
Em uma central geotérmica binária, o fluido de trabalho isobutano deve ser condensado pelo ar em um condensador a com uma taxa de . O ar entra no condensador a e deixa-o a .
A transferência de calor com base na superfície do lado do isobutano é de . Determine a vazão mássica do ar e o coeficiente global de transferência de calor.
Passo 1
A vazão mássica de ar (fluido frio) pode ser calculada da seguinte forma:
Enquanto o coeficiente global de transferência de calor pode ser calculado por:
De qualquer forma, precisaremos da taxa de transferência de calor e da diferença de temperatura média logarítmica.
Passo 2
A taxa de transferência de calor pode ser calculada da seguinte forma:
Substituindo os valores, teremos:
Passo 3
Para a diferença de temperatura média logarítmica, teremos:
Logo:
Obs.: Como há mudança defase em um dos fluidos, o fator de correção será . Então não precisamos nos preocupar com ele nesses casos.
Passo 4
A vazão mássica de ar (fluido frio) será:
Substituindo os valores:
Passo 5
O coeficiente global de transferência de calor será:
Substituindo os valores, onde :
Resposta
Exercício Resolvido #6
ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.
A água entra nos tubos de de diâmetro interno de um trocador de calor de tubo duplo em contracorrente a com uma taxa de . Ela é aquecida pela condensação de vapor a no casco.
Se o coeficiente global de transferência de calor é de , determine o comprimento do tubo necessário a fim de aquecer a água a .
Passo 1
Para calcular o comprimento do tubo, teremos que usar essa expressão:
Onde , logo:
Vamos precisar calcular a taxa de transferência de calor, a média logarítmica das temperaturas e o fator de correção.
Passo 2
Como o problema já nos deu a vazão mássica e as temperaturas de entrada e saída da água, a taxa de transferência de calor será dada por:
Substituindo os valores:
Passo 3
A média logarítmica das diferenças de temperatura é dada por:
Logo:
Como já estamos tratando de um trocador contracorrente, .
Passo 4
Finalmente, o comprimento necessário será:
Resposta
Exercício Resolvido #7
ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.
(Adaptado) O ar deve ser preaquecido por gases em um trocador de calor de escoamento cruzado antes de entrar em um forno. O ar entra no trocador de calor a , com na taxa de , e sai a .
Gases de combustão entram a com uma taxa de e saem a . O coeficiente global de transferência de calor baseado nos tubos é de .
Considerando ambos os fluidos sem mistura, determine a taxa de transferência de calor e a área de troca térmica.
Passo 1
Como o problema já nos deu a vazão mássica de gás de combustão e as temperaturas de entrada e saída, a taxa de transferência de calor será dada por:
Substituindo os valores:
Passo 2
Para calcular a superfície de transferência de calor, teremos que usar essa expressão:
Agora vamos precisar calcular a média logarítmica das temperaturas!
Passo 3
Começando pela média logarítmica, temos que:
Logo:
Passo 4
Dessa forma, a área de troca térmica será:
Resposta
Exercício Resolvido #8
ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.
Um trocador de calor casco e tubo com 2 passes no casco e 12 passes no tubo é utilizado para aquecer a água com etileno glicol .
A água entra no tubo a com uma taxa de e deixa-o a . O etileno glicol entra no casco a e deixa-o a .
Se o coeficiente global de transferência de calor baseado no lado do tubo é de , determine a taxa de transferência de calor e a superfície de transferência de calor no lado do tubo.
Passo 1
Já que o problema nos deu a vazão mássica da água, bem como as suas temperaturas de entrada e saída, a taxa de transferência de calor pode ser calculada da seguinte forma:
Substituindo os valores:
Passo 2
Para calcular a superfície de transferência de calor, teremos que usar essa expressão:
Vamos precisar calcular a média logarítmica das temperaturas e o fator de correção.
Passo 3
Começando pela média logarítmica, temos que:
Logo:
Passo 4
Para o fator de correção, teremos:
Levando em consideração que temos 2 passes de casco e 12 passes nos tubos, de acordo com o gráfico abaixo:
Passo 5
Dessa forma, a área de troca térmica será:
Resposta
Exercício Resolvido #9
Questão 2, PUC, P3-2003
Considere um trocador de calor em escoamento cruzado, que consiste no escoamento externo de ar (fluido misturado) sobre um conjunto de 30 tubos de diâmetros iguais a . Ar atmosférico entra no trocador a com vazão mássica igual a (considere para o ar, e ).
Água quente entra pelos tubos a temperatura de e velocidade igual a , e sai a temperatura de (considere para a água, e ). Considere que o coeficiente global de troca de calor é igual a .
Determine:
O fluxo de calor trocado entre os fluidos.
A temperatura de saída do ar.
A área do trocador de calor.
Passo 1
A taxa de transferência de calor trocado entre os fluidos.
Como temos as temperaturas de entrada e saída do fluido quente, podemos determinar a taxa de transferência de calor da seguinte forma:
Substituindo os valores:
Passo 2
A temperatura de saída do ar.
A temperatura de saída do ar pode ser calculada por:
Passo 3
A área do trocador de calor.
Nesse caso, vamos utilizar a seguinte equação:
Onde a diferença de temperatura média logarítmica é dada por:
Sendo:
Assim:
Para um trocador de escoamento cruzado, . Logo:
Resposta
Exercício Resolvido #10
Questão 1, PUC, P3-2006
Um trocador de calor em escoamento cruzado não aletado é utilizado para resfriar óleo de a . O óleo entra pelos tubos a uma velocidade média igual a . São utilizados no trocador 5 tubos, com diâmetro igual a .
Ar é utilizado como fluido de resfriamento, entrando no trocador a e escoando a uma vazão de . Calcule:
O coeficiente global de troca de calor, desprezando a espessura da parede dos tubos, e considerando que o coeficiente de troca de calor externo vale .
A temperatura de saída do ar e a diferença média logarítmica de temperatura.
O comprimento dos tubos, utilizando o método da diferença média logaritmica.
Passo 1
O coeficiente global de troca de calor, desprezando a espessura da parede dos tubos, e considerando que o coeficiente de troca de calor externo vale .
Desprezando a espessura da parede dos tubos, o coeficiente global de troca de calor será calculado a partir dos coeficientes convectivos interno e externo, da seguinte forma:
Novamente, como estamos desconsiderando a espessura do tubo, . Dessa forma:
Dessa equação, temos tudo, exceto o coeficiente convectivo interno.
Passo 2
Para a convecção interna, o número de Reynolds será dado por:
Assim, como o óleo está sendo resfriado o número de Nusselt será dada por:
Dessa forma, o coeficiente convectivo interno será:
Assim, o coeficiente global de transferência de calor será:
Passo 3
A temperatura de saída do ar e a diferença média logarítmica de temperatura.
A temperatura de saída do ar pode ser calculada por:
Onde a taxa de transferência de calor é dada por:
Substituindo os valores:
Dessa forma, a temperatura de saíta do ar será:
Passo 4
A diferença média logarítmica de temperatura é dada por:
Sendo:
Assim:
Passo 5
O comprimento dos tubos, utilizando o método da diferença média logaritmica.
A taxa de transferência de calor pode ser calculada da seguinte forma:
Onde o fator de forma é calculado a partir do gráfico considerando um fluido misturado e o outro não misturado, onde:
Assim:
Dessa forma, o comprimento dos tubos será:
Resposta
,