Método da Eficiência e NUT
Produzido por Giovanna RonzéTeoria
Introdução
Quando temos um trocador de calor onde conhecemos o coeficiente global de transferência de calor e suas temperaturas de entrada e saída, podemos determinar a taxa de transferência de calor através das seguintes equações:
Ou pelo Método da Diferença Logarítmica, dado por:
Onde é a diferença de temperatura média logarítmica, dada por:
Repare que nas três equações para a taxa de transferência de calor, nós precisamos saber as temperaturas de entrada e saída.
Agora, e se não tivermos as temperaturas de saída dos fluidos frio e quente?!
Vamos pensar na seguinte situação: óleo quente deve ser resfriado com água em um trocador de calor casco e tubo com 2 passes no casco e 12 passes nos tubos.
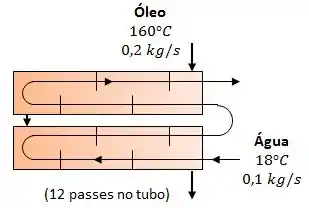
Os tubos são de paredes finas e são feitos de cobre com um diâmetro de . O comprimento de cada passe de tubo do trocador é de e o coeficiente global de transferência de calor é de .
O que queremos aqui é determinar a taxa de transferência de calor.
Nesse caso, como o método da média logarítmica não vai resolver a nossa vida, o método mais adequado é o Método da Eficiência e NUT.
Qual é a ideia desse método?!
Bom, ele basicamente se baseia em um parâmetro adimensional chamado efetividade da transferência do calor , definidor por:
![]()
Onde corresponde à taxa de transferência de calor real (que é quem queremos calcular), dada por:
Em que e são as taxas de capacidade térmica dos fluidos quente e frio, respectivamente.
Enquanto corresponde à taxa de transferência de calor máxima possível, dada por:
![]()
Onde é o menor valor entre e .
Olhando pro nosso problema, vamos calcular as taxas de capacidade térmica, ver quem é menor, e calcular a taxa de transferência de calor máxima possível.
Como a taxa de capacidade térmica do fluido frio é menor:
Dessa forma, a taxa de transferência de calor máxima possível será:
![]()
Até aqui, está tudo muito lindo.
Mas como calculamos a efetividade da transferência de calor?!
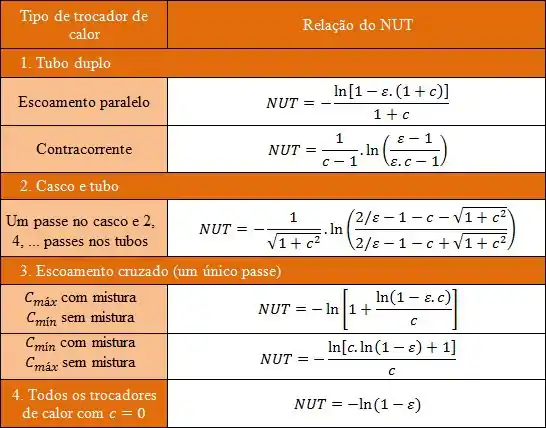
A efetividade da transferência de calor é calculada a partir de uma série de relações, que dependem basicamente das condições do trocador de calor, se liga:

Obs.: O caso (4) é utilizado quando há mudança de fase em um dos fluidos! #ficadica
Opa! Aparecem duas grandezas que precisamos saber pra calcular a efetividade.
A primeira delas é o Número de Unidades de Transferência, ou NUT (Tcharaaam!!!), que é dado por:
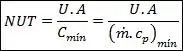
A segunda grandeza que vamos precisar pra calcular a efetividade é a razão das capacidades , dada por:
![]()
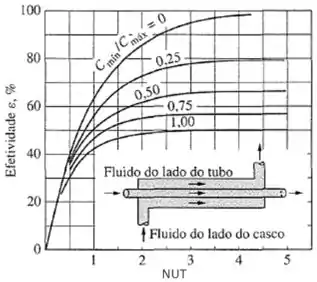
A efetividade também pode ser encontrada por meio de gráficos. Então prometo coloca-los nos final desse capítulo, caso você prefira. Ok?
Agora, caso nós tenhamos a efetividade e quisermos calcular o NUT, podemos usar a tabela abaixo:
Voltando ao nosso problema...
Bom, como já fomos devidamente apresentados ao NUT, sabemos que ele é dado por:
No nosso caso, temos o coeficiente global de transferência de calor e a taxa de capacidade térmica mínima . A área total de transferência de calor será:
Onde corresponde ao número de passes no tubo. Logo, o NUT será:
![]()
Já a razão das capacidades será dada por:
![]()
Como estamos trabalhando com um trocador de casco e tubo, com 12 passes no tubo, de acordo com a nossa tabela, a relação mais adequada para a efetividade será:
Substituindo os valores de e , teremos:
Finalmente, a taxa de transferência de calor real será:
![]()
Agora já estamos prontos pra cair nos exercícios. Mas antes...
Promessa é dívida!
Como eu prometi quando falamos da efetividade, vou colocar aqui pra você os gráficos que podem ser utilizados pra calcular a efetividade.
Para trocador de calor de escoamento paralelo:
Para trocador de calor de escoamento contracorrente:
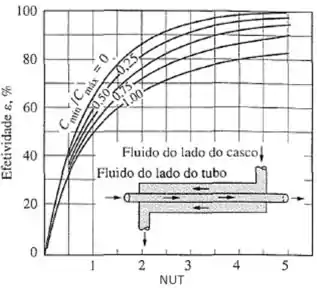
Para trocador de calor de calor casco e tubo, com um passe no casco e 2, 4, 6, ... passes nos tubos:
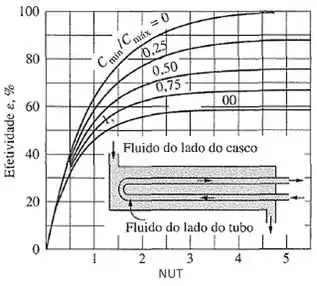
Para trocador de calor de calor casco e tubo, com um passe no casco e 4, 8, 12, ... passes nos tubos:
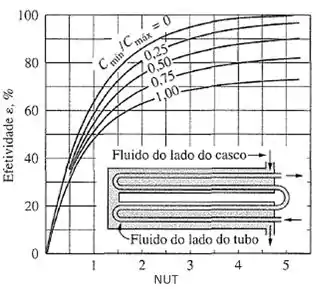
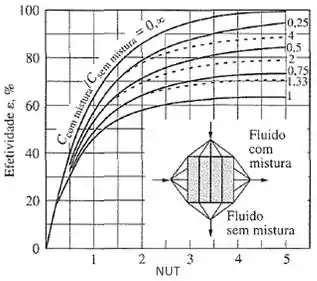
Para trocador de calor de escoamento cruzado com dois fluidos sem mistura:
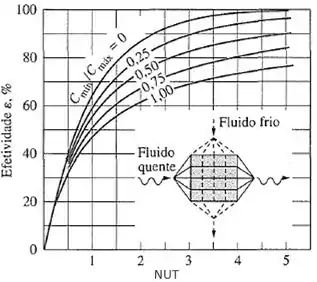
Para trocador de calor de escoamento cruzado com um fluido com mistura e o outro sem mistura:
Qual é a ideia desse método?!
Mas como calculamos a efetividade da transferência de calor?!
Voltando ao nosso problema...
Promessa é dívida!
Exercícios Resolvidos
Exercício Resolvido #1
ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.
Um trocador de calor de tubo duplo com parede fina e escoamento paralelo é utilizado para aquecer um produto químico, cujo calor específico é , com água quente .
O produto químico entra a com uma taxa de , enquanto a água entra a com uma taxa de . A superfície de transferência de calor do trocador de calor é de e o coeficiente global de transferência de calor é .
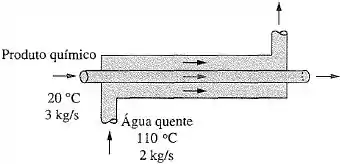
Determinar as temperaturas de saída do produto químico e da água.
Passo 1
As temperaturas de saída podem ser calculadas pelas seguintes equações:
Show de bola! Nós temos as temperaturas de entrada dos fluidos, temos como calcular as taxas de capacidade térmica, mas não temos a taxa de transferência de calor.
Então vamos atrás desse cara usando o Método da Eficiência e NUT. Dessa forma, a taxa de transferência de calor será dada por:
Vamos tratar de cada termo separadamente, beleza?
Passo 2
Vamos começar tratando da taxa de transferência de calor máxima possível , que é dada por:
Para calcular a menor taxa de capacidade térmica, temos que calcular as taxas de capacidade térmica dos dois fluidos.
Como o menor valor corresponde ao do fluido frio (água), teremos:
Dessa forma, a taxa de transferência de calor máxima possível será:
![]()
Passo 3
Para calcular a efetividade da transferência de calor, vamos precisar do NUT e da razão das capacidades, dados por:
Como estamos trabalhando com um trocador de calor de escoamento paralelo, a relação mais adequada para a efetividade será:
Substituindo os valores:
![]()
Passo 4
A taxa de transferência de calor será:
Assim, as temperaturas de saída dos fluidos serão:
![]()
![]()
Resposta
Exercício Resolvido #2
ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.
Um trocador de calor de escoamento cruzado ar-água com uma eficiência de é utilizado para aquecer água com ar quente .
A água entra no trocador de calor a com uma taxa de , enquanto o ar entra a com uma taxa de .
Se o coeficiente global de transferência de calor baseado no lado da água é de , determinar a superfície de transferência de calor do trocador de calor no lado da água.
Considere que ambos os fluidos são sem mistura.
Passo 1
Vamos começar pensando em qual é a melhor maneira de encontrar a área superficial de transferência de calor.
Podemos pensar na equação da taxa de transferência de calor:
Opa! Mas como não temos a temperatura de saída dos fluidos, então essa não é uma boa.
Uma outra equação que associa a área superficial é justamente a fórmula do NUT, dada por:
Essa parece ser boa! Mas vamos precisar encontrar o NUT e a menor taxa de capacidade térmica.
Vamos atrás deles então.
Passo 2
Começando pelas taxas de capacidade térmica, temos que:
Como o menor valor corresponde ao do fluido frio (água), teremos:
![]()
Passo 3
Temos algumas equações para calcular o NUT, mas vamos precisar da efetividade de transferência de calor e da razão das taxas de capacidade térmica, dada por:
Estamos trabalhando com um trocador de calor de escoamento cruzado, onde ambos os fluidos são sem mistura. Nesse caso, não temos uma equação para o NUT na nossa tabela, então vamos utilizar o gráfico adequado.
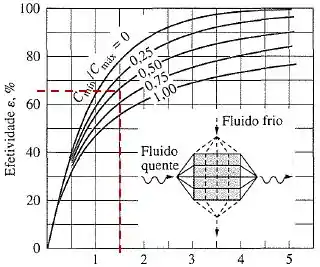
Logo:
![]()
Passo 4
Finalmente, a área de troca térmica será:
![]()
Resposta
Exercício Resolvido #3
ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.
(Adaptado) A água entra nos tubos de de diâmetro interno de um trocador de calor de tubo duplo em contracorrente a com uma taxa de . Ela é aquecida por condensação de vapor a no casco.
Se o coeficiente global de transferência de calor do trocador é de , determinar o comprimento do tubo necessário, a fim de aquecer a água a utilizando o Método da Eficiência e NUT.
Passo 1
Pelo Método da Eficiência e NUT, a área de troca térmica pode ser encontrada através da expressão do NUT:
Como estamos trabalhando com uma área cilíndrica, temos que:
Substituindo a expressão que acabamos de encontrar para :
Dessa equação, não temos o NUT e nem a menor taxa de capacidade térmica . Então vamos atrás deles!
Passo 2
Como o fluido quente está passando por uma mudança de fase (temperatura constante), haverá variação de temperatura somente no fluido frio, de forma que:
![]()
Passo 3
Temos algumas equações para calcular o NUT, mas vamos precisar da efetividade de transferência de calor e da razão das taxas de capacidade térmica.
A efetividade pode ser calculada através da seguinte equação:
Onde:
Dessa forma, a efetividade será:
Como há mudança de fase no fluido quente, a razão das capacidades será nula . Assim, a relação mais adequada para o NUT será:
![]()
Passo 4
Finalmente, o comprimento do tubo necessário será:
![]()
Resposta
Exercício Resolvido #4
ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.
Água deve ser aquecida com ar quente aquecido por energia solar em um trocador de calor de tubo duplo em contracorrente.
O ar entra no trocador de calor a com uma taxa de , enquanto a água entra a com uma taxa de . O coeficiente global de transferência de calor baseado na face interna do tubo é .
O comprimento do tubo é de e seu diâmetro interno é de . Determinar as temperaturas de saída da água e do ar.
Passo 1
As temperaturas de saída podem ser calculadas pelas seguintes equações:
Show de bola! Nós temos as temperaturas de entrada dos fluidos, temos como calcular as taxas de capacidade térmica, mas falta a taxa de transferência de calor.
Usando o Método da Eficiência e NUT, a taxa de transferência de calor será dada por:
Vamos tratar de um termo de cada vez aqui.
Passo 2
Começando pela taxa de transferência de calor máxima possível , que é dada por:
Para calcular a menor taxa de capacidade térmica, temos que calcular as taxas de capacidade térmica dos dois fluidos.
Como o menor valor corresponde ao do fluido quente (ar), teremos:
Dessa forma, a taxa de transferência de calor máxima possível será:
![]()
Passo 3
Para calcular a efetividade da transferência de calor, vamos precisar do NUT e da razão das capacidades, dados por:
Como estamos trabalhando com um trocador de calor de escoamento contracorrente, a relação mais adequada para a efetividade será:
Substituindo os valores:
Passo 4
A taxa de transferência de calor será:
![]()
Assim, as temperaturas de saída dos fluidos serão:
![]()
![]()
Resposta
Exercício Resolvido #5
ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.
O vapor deve ser condensado sobre o lado do casco de um condensador com 1 passe no casco e 8 passes no tubo, com 50 tubos em cada passe, a .
A água de resfriamento entra nos tubos a com uma taxa de . Os tubos são de parede fina e têm um diâmetro de e de comprimento por passe.
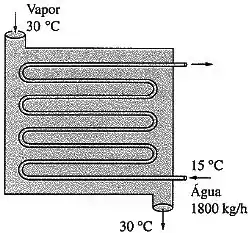
Se o coeficiente global de transferência de calor é de , determinar a taxa de transferência de calor e a taxa de condensação do vapor.
Passo 1
Determinar a taxa de transferência de calor.
Como não temos as temperaturas de saída, vamos com o Método da Eficiência e NUT. Assim, podemos calcular a taxa de transferência de calor da seguinte forma:
Vamos calcular cara um desses termos separadamente.
Passo 2
A taxa de transferência de calor máxima possível é dada por:
Como o fluido quente está passando por uma mudança de fase (temperatura constante), haverá variação de temperatura somente no fluido frio, de forma que:
Onde . Logo:
Dessa forma, a taxa de transferência de calor máxima possível será:
![]()
Passo 3
Para calcular a efetividade da transferência de calor vamos precisar calcular o NUT e a razão das capacidades .
O NUT é dado por:
Onde a área de troca térmica será:
Assim, o NUT será:
E como um dos fluidos está em mudança de fase, .
Assim, a relação para a efetividade apropriada será:
![]()
Passo 4
Finalmente, a taxa de transferência de calor real será:
![]()
Passo 5
Determinar a taxa de condensação do vapor.
Agora que já temos a taxa de transferência de calor, podemos encontrar a taxa de condensação do vapor através da seguinte equação:
Substituindo os valores:
![]()
Resposta
Exercício Resolvido #6
Questão 1, PUC, P3-2003
Num trocador de calor de tubos concêntricos e correntes paralelas, água fria entra pelo tubo interno a e a uma vazão de . Óleo quente entra a , e escoa a uma taxa de , através do espaço anular entre os tubos.
O tubo interno tem um diâmetro interno igual a e espessura igual a . O tubo externo tem diâmetro igual a . O comprimento dos tubos é igual a e a condutividade térmica dos tubos vale . As propriedades da água são dadas por: , , , , . Determine:
O coeficiente de troca de calor interno, considerando escoamento desenvolvido.
O coeficiente global de troca de calor baseado na área interna do tubo interno, considerando que o coeficiente de troca de calor externo do tubo vale .
A efetividade do trocador de calor.
A taxa de transferência de trocador entre os fluidos e a temperatura de saída da água.
Passo 1
O coeficiente de troca de calor interno, considerando escoamento desenvolvido.
Para a convecção interna, o número de Reynolds será dado por:
Assim, calculamos o número de Nusselt pela correlação de escoamento turbulento e plenamente desenvolvido:
Dessa forma, o coeficiente convectivo interno será:
![]()
Passo 2
O coeficiente global de troca de calor baseado na área interna do tubo interno, considerando que o coeficiente de troca de calor externo do tubo vale .
Como não estamos considerando fatores de deposição no nosso trocador e ele não possui aletas, podemos calcular o coeficiente global de transferência de calor dessa forma:
No nosso caso, estamos interessados em calcular o coeficiente global em relação à superfície interna, logo:
Como temos uma superfície cilíndrica, a resistência térmica de condução será, substituindo os valores:
Substituindo todos os valores na expressão do coeficiente global, vamos encontrar o seguinte:
Onde e .
Passo 3
A efetividade do trocador de calor.
Como estamos trabalhando com um caso de trocador de calor duplo com escoamento paralelo, a efetividade é dada por:
Onde e são dados por:
Onde as taxas de capacidade térmica são dadas por:
Dessa forma:
Assim, a efetividade será:
Passo 4
A taxa de transferência de trocador entre os fluidos e a temperatura de saída da água.
Podemos usar a efetividade pra calcular a taxa de transferência de calor da seguinte forma:
Passo 5
A temperatura de saída da água pode ser calculada da seguinte forma:
![]()
Resposta
;
Exercício Resolvido #7
Questão 2, PUC, P3-2006
(Adaptado) Num trocador de calor de tubos concêntricos e correntes contrárias, água fria entra pelo tubo interno a e sai a . Água quente escoa pelo espaço anular, entrando a e a uma velocidade de .
O tubo interno tem um diâmetro igual a , o tubo externo tem diâmetro interno igual a e a espessura da parede do tubo interno é igual a . O comprimento dos tubos é igual a . Sabe-se que a efetividade do trocador é igual a .
As propriedades da água são consideradas constantes, dadas por: . Determine:
O fluxo de calor trocado entre os fluidos e a temperatura de saída da água quente.
A vazão mássica de água fria.
Passo 1
O fluxo de calor trocado entre os fluidos e a temperatura de saída da água quente.
Podemos calcular o fluxo de calor a partir da efetividade da seguinte forma:
Substituindo com os dados que já conhecemos, ficamos com:
Onde a área vai ser dada pela diferença entre a área do tubo externo e a do tubo interno somado à sua espessura:
Assim, substituindo os valores:
Passo 2
A temperatura de saída da água quente pode ser calculada reorganizando a equação da taxa de calor trocado da seguinte forma:
Como já conhecemos todos os dados, é só substituir e calcular:
Passo 3
A vazão mássica de água fria.
Para determinar a vazão mássica de água fria, vamos usar a equação da taxa de calor trocado pelo fluido frio:
Dessa forma:
Resposta