Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Energia Específica e escoamento sobre elevação

Ver Todos os Exercícios

Teoria

Profundidade Crítica

Fala time!

Hoje vou te mostra um novo negócio, ele é um pouquinho abstrato no início, mas depois vai fazer mais sentido.

Vou tentar te dar uma ideia do ponto que a gente vai chegar no final. Já percebeu que em alguns rios a gente tem a formação de ondas?

Isso aí acontece principalmente pela geometria do fundo do rio, pela profundidade do escoamento e pela velocidade. Mas vamos com calma, um passo de cada vez

Então se lembra da equação da energia?

z 1 + V 1 ² 2 g + p 1 ρ g = z 2 + V 2 ² 2 g + p 2 ρ g + h p

Em canais abertos somente as componentes de velocidade V 1 ² 2 g e elevação z 1 que influenciam na energia do sistema. Isso acontece por que a pressão é a atmosférica em todos pontos.

Mas o importante é entender que o nome da equação é por que realmente representa a energia do sistema. Mais especificamente a energia específica:

E = y + V ² 2 g

Repare que mudei umas coisinhas. Ao invés da elevação vamos falar da profundidade y e da velocidade do escoamento V , e vamos supor que não temos atrito.

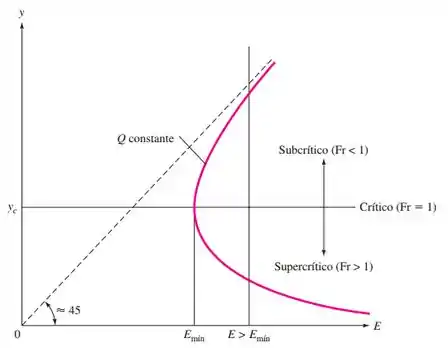
Em todo escoamento desse tipo, existe uma energia mínima E m i n que nos dará uma informação valiosa sobre o escoamento, a profundidade crítica.

Vamos analisar um caso simples de um canal retangular, vamos escrever a expressão da energia específica toda em funç��o de y .

Lembre-se que Q = V A , e no retângulo A = b y , logo,

Q = V b y   o u   Q b y = V

Substituindo na expressão:

E = y + Q ² 2 g b ² y ²

Vamos derivar E em y e igualar a zero:

d E d y = 0

1 - 2 Q 2 2 g b 2 y 3 = 0

Logo

1 = Q 2 g b 2 y 3

y = y c = Q 2 g b 2 1 / 3

Este valor de y é a profundidade crítica, que costumamos chamar de y c .

Isso vai ajudar a gente a dizer se o escoamento é crítico, subcrítico ou supercrítico. E isso tem tudo a ver com um fator adimensional chamado número de Froude.

Um escoamento estar em regime supercrítico significa que temos variações de elevação na superfície livre ou simplesmente ondas. E isso tem algumas implicações em como analisaremos o escoamento.

Antes vou explicar rapidinho o que é esse tal Froude.

Número de Froude

Lembra do número de Reynolds, que além de outras coisas dizia se um escoamento é laminar, de transição ou turbulento?

Existe outro adimensional, chamado número de Froude:

F r = V V o n d a = V g y

Ele vai nos dizer se o escoamento é subcrítico, crítico ou supercrítico, ou seja se a velocidade do escoamento é menor, igual ou maior a velocidade da onda que se propaga no fluido.

Escoamento sem atrito sobre uma elevação

Isso tudo que a gente viu serve pra gente analisar o seguinte problema:

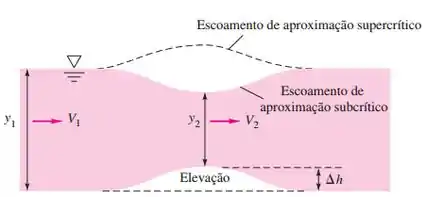
Se temos um escoamento supercrítico o nível do fluido sobe quando passa por uma elevação.

E se está em regime subcrítico, o nível do fluido diminui.

As equações que regem esse problema são:

A equação da continuidade:

Q 1 = Q 2

V 1 y 1 b = V 2 y 2 b

V 1 y 1 = V 2 y 2

E a equação da energia:

E 1 = E 2 + ∆ h

y 1 + V 1 ² 2 g = y 2 + V 2 ² 2 g + ∆ h

Substituindo uma na outra e ajeitando as coisas:

y 2 ³ - V 1 2 2 g + y 1 - ∆ h y 2 2 + V 1 2 y 1 ² 2 g = 0

Vamos praticar um pouco porque hoje teve muita informação pra digerir.

Número de Froude

Escoamento sem atrito sobre uma elevação

Exercícios Resolvidos

Exercício Resolvido #1

Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.

Água a 20 ° C escoa em um canal retangular de 30 cm de largura a uma profundidade de 10   c m e uma vazão de 80000   c m 3 / s . Calcule ( a )   o número de Froude e ( b ) o número de Reynolds.

Passo 1

A expressão do número de Froude é:

F r = V g y

Onde y é a profundidade, V a velocidade do escoamento e g a gravidade.

y é dado no enunciado:

y = 10   c m = 0,1   m

g = 9,81   m / s ²

Falta calcularmos V .

Passo 2

O enunciado nos fornece as dimensões do canal e a vazão. Lembrando que:

V = Q / A

Substituindo os valores conhecidos:

V = 80000   c m ³ / s 30   c m × 10   c m

V = 266,67 c m s = 2,67   m / s

Logo o número de Froude é:

F r = 2,67 9,81 × 0,1

F r = 2,696

Passo 3

O número de Reynolds relativo a profundidade R e y é igual a

R e y = ρ V y μ

Propriedades da água:

ρ = 1000 k g m 3

μ = 0,001 k g m . s

Logo

R e y = 1000 × 2,67 × 0,01 0,001

R e y = 26700

Resposta

F r = 2,696

R e y = 26700

Exercício Resolvido #2

Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.

Um canal circular em asfalto, com 75 cm de diâmetro, está escoando com meia carga a uma velocidade média de 3,4 m/s. Calcule (a) a vazão volumétrica, (b) o número de Froude e (c) a declividade crítica.

Dica: deduzir a expressão da energia específica para qualquer seção.

Passo 1

Neste exercício temos uma seção diferente de uma retangular, logo não podemos usar a expressão da profundidade crítica que calculamos. Portanto para encontrarmos a profundidade crítica deveremos relacionar a expressão que deduziremos e a fórmula de Manning.

No caso a letra a é resolvida claculando a vazão Q = V A

V = 3,4 m s

A = π 0,375 2 2 = 0,22   m ²

Q = 3,4 × 0,22 = 0,75   m ³ / s

Passo 2

Neste exercício vamos deduzir a expressão da profundidade crítica em um caso geral e aplicar ao nosso problema. Ela será necessária para calcularmos as letras ( b ) e ( c ) .

Dada a equação da energia específica:

E = y + V ² 2 g

No nosso caso devemos escrever a velocidade como V = Q A . Logo,

E = y + Q ² 2 g A ²

Supondo Q constante e A = A ( y ) , vamos derivar ambos os lado em y d E d y = 1 - 2 Q ² 2 g 1 A ³ d A d y

d E d y = 1 - Q ² g 1 A ³ d A d y

Para encontrarmos a “área crítica”, d E d y = 0 ,

0 = 1 - Q ² g 1 A ³ d A d y

1 = Q ² g 1 A ³ d A d y

d A d y = g A ³ Q ²

Sendo d A = b 0 d y , em que b 0 é a largura do canal na superfície livre.

b 0 d y d y = g A ³ Q ²

A ³ = b 0 Q ² g

A área crítica é portanto:

A c = b 0 Q ² g 1 / 3

Lembrando que Q = V A

Podemos calcular a velocidade crítica V c

V c = g A c ³ b 0 1 / 2 A c = g A c b 0 1 / 2

O interessante da velocidade crítica é que podemos tirar as seguintes conclusões sobre a profundidade crítica:

V < V c ,     y > y c : e s c o a m e n t o   s u b c r í t i c o ,   F r < 1

V = V c ,     y = y c : e s c o a m e n t o   c r í t i c o ,   F r = 1

V > V c ,     y < y c : e s c o a m e n t o   s u p e r c r í t i c o ,   F r > 1

Pela expressão do número de Froude, podemos concluir que

F r = V g y = V V c

Logo nosso número de Froude do exercício depende da velocidade crítica:

V c = g A c b 0 1 / 2 = 9,81 × 0,22 0,75 1 / 2

V c = 1,7   m / s

Logo o Froude é

F r = V V c = 3,4 1,7 = 2

Passo 3

Agora aplicaremos a expressão da velocidade crítica a fórmula de Manning para descobrirmos a declividade crítica:

V = R h 2 / 3 S 0 1 / 2 n   o u   S c = V c ² n ² R h 4 / 3

S c = g A c b 0 n R h 2 / 3 2

Que após algumas manipulações e substituições ficamos com a relação abaixo:

S c = n ² g R h 1 / 3 P m b 0 = f 8 P m b 0

n do asfalto é 0,016 e vamos utilizar a relação:

S c = V c ² n ² R h 4 / 3

Calcularemos R h :

R h = π R ² 2 π R = R 2 = 0,1875   m

Logo a declividade é igual a:

S c = 1,7 ² 0,016 ² 0,1875 4 / 3 = 0,0069

Resposta

a   Q = 0,75 m 3 s

b   F r = 2

c   S c = 0,0069

Exercício Resolvido #3

Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.

Um rio largo, com leito em terra limpa, tem uma vazão q   =   13,94   m 3 / ( s ∙ m ) . Qual a profundidade crítica? Se a profundidade real for de 3,66 m, qual será o número de Froude do rio? Calcule a declividade crítica ( a )   pela fórmula de Manning e ( b ) pelo diagrama de Moody.

Passo 1

A vazão q é a vazão por unidade de largura b do canal, ou seja:

q = Q b

Para calcularmos a profundidade crítica aplicamos na fórmula:

y c = Q 2 g b 2 1 3

Trocando Q ² / b ² por q ² :

y c = q ² g 1 3

y c = 13,94 ² 9,81 1 3

y c = 2,71   m

Passo 2

Calculamos o número de Froude para y = 3,66   m :

F r = V g y

Podemos escrever q = V y , porque Q = V A = V b y

F r = q / y g y

F r = 13,94 / 3,66 9,81 × 3,66

F r = 0,64

Passo 3

Agora devemos avaliar a declividade usando a fórmula de Manning, que aplicada a canais largos é:

S c ≈ f 8 P m b 0 ≈ f 8

Isso se deve ao fato do perímetro molhado ser praticamente igual a largura na superfície livre, logo podemos aproximar a outra expressão que usa n para a expressão:

S c ≈ f 8 ≈ n 2 g y c 1 3

n para rios com leito em terra limpa 0,030

S c = 0,03 ² × 9,81 8,87 1 / 3

S c = 0,0043

Passo 4

Agora calculando pelo diagrama de Moody, vamos usar aquela fórmula lá de trás:

1 f 1 / 2 = - 2   log ⁡ ϵ / d 3,7

Sendo ϵ = 37   m m e d = y = 3,66   m

1 f 1 / 2 = - 2   log ⁡ 0,037 / 3,66 3,7

1 f 1 / 2 = 5,13

f = 0,038

Se S c = f 8 :

S c = 0,038 8

S c = 0,0047

Resposta

y c = 2,71   m

F r = 0,64

a Por Manning S c = 0,0043

b Por Moody S c = 0,0047

Exercício Resolvido #4

Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.

Na Figura, seja V 0 = 1   m / s e y 0 = 1   m . Se a altura máxima da elevação for de 15 cm, calcule (a) o número de Froude sobre o topo da elevação e (b) a depressão máxima na superfície da água.

Passo 1

Vamos falar um pouco agora sobre o escoamento sobre elevações.

Podemos analisar esse problema simplesmente aplicando nossa equação da energia que aplica esta variação de altura:

y 2 ³ - V 0 2 2 g + y 0 - ∆ h y 2 2 + V 0 2 y 0 ² 2 g = 0

Conhecemos

V 0 = 1 m s

y 0 = 1   m

∆ h = 0,15   m

Logo a equação se torna:

y 2 ³ - 1 2 × 9,81 + 1 - 0,15 y 2 2 + 1 2 × 9,81 = 0

y 2 ³ - 0,9 y 2 2 + 0,051 = 0

Podemos resolver esta equação de terceiro grau usando algum método númerico ou podemos realizar uma aproximação que 0,051 ≈ 0 .

Logo,

y 2 3 = 0,9 y 2 2

y 2 ≈ 0,9

Se diminuirmos um pouco este valor de y 2 podemos chegar a um valor mais preciso. Por exemplo se aplicamos y 2 = 0,8 a parte direita da equação se torna - 0,013 , um número mais próximo de zero que o anterior.

Passo 2

Para calcularmos o Froude devemos calcular V 2 , supondo vazão constante:

V 2 y 2 = V 0 y 0

Logo V 2   é

V 2 = V 0 y 0 y 2 = 1 0,8

V 2 = 1,25   m / s

Portanto nosso Froude é igual a

F r = V 2 g y 2 = 1,25 9,81 × 0,8

F r = 0,45

Passo 3

Na letra ( b ) o problema se torna geométrico apenas, sabemos que pela figura:

y 0 = y 2 + ∆ h + ∆ z

Sendo ∆ z a diminuição no nível da superfície livre:

1 = 0,8 + 0,15 + ∆ z

∆ z = 0,05   m

Resposta

a   F r = 0,45

b ∆ z = 0,05   m

Exercício Resolvido #5

Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 774, ex. 11.16

Encontre a profundidade crítica de um canal retangular de comprimento 2,5 m para uma vazão de 3 m³/s.

Passo 1

Olááá! Vimos na teoria que para calcular a profundidade crítica y c em canal retangular podemos usar essa fórmula

y c = Q 2 g b 2 1 / 3

Repara que essa fórmula é válida especificamente para o canal retangular, pois para obtê-la tivemos que colocar a geometria. Como é nosso caso, estamos aplicando. :D

O enunciado informou que o comprimento b é 2,5 m e a vazão Q é 3 m³/s. Substituindo na expressão da profundidade crítica para o canal retangular

y c = 3 2 9,8 × 2,5 2 1 / 3

y c = 3 2 9,8 × 2,5 2 1 / 3

y c = 0,528   m

Então a profundidade crítica é 0,528 m. Bora praticar mais?

Resposta

y c = 0,528   m

Exercício Resolvido #6

Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 774, ex. 11.15

Para um canal retangular de largura b = 20 m, construa uma família de curvas de energia específica para Q = 0,25, 75, 125 e 200 m³/s. Quais são as energias específicas mínimas para essas curvas?

Passo 1

Nesse exercício, vamos entender melhor o comportamento da energia específica no canal retangular.

Escrevendo a equação da energia em função da profundidade do escoamento e considerando que a pressão não variae que não há perda por atrito, temos

E = y + V ² 2 g

Podemos escrever a energia em função da vazão, usando V = Q / A . Como nosso caso é um canal retangular

V = Q b y

E assim, atualizando a equação da energia

E = y + Q ² 2 g b ² y ²

Sabemos que g é a gravidade e o comprimento b é 20 m

E = y + Q ² 2 × 9,8 × 20 ² y ²

E = y + Q ² 7840 y ²

Bem, essa é a equação, mas o enunciado pede uma família dela! Vamos conseguir várias curvas pois para cada uma delas vamos substituir uma vazão Q diferente (também dada no enunciado). Beleza?

As curvas da família são

E = y + 0 ² 7840 y ²

E = y + 25 ² 7840 y ²

E = y + 7 5 ² 7840 y ²

E = y + 12 5 ² 7840 y ²

E = y + 200 ² 7840 y ²

Lembrando que o formato geral dessas curvas é

Para fazer as diferentes famílias de curvas, vamos montar uma tabela com as energias específicas para cada vazão volumétrica.

Com isso, já podemos montar o gráfico. Mas antes, atenção! A energia específica fica no eixo x e a profundidade no eixo y! Se colocar ao contrário, o formato da curva vai ficar diferente. Vamos ficar atentas!

A forma dessas curvas é a mesma que vimos na teoria. Deu tudo certo! Repara que quanto maior a vazão, maior é a energia específica mínima (o ponto em que a curva muda de direção)

Passo 2

O exercício também pediu a energia específica mínima de cada curva. Como se trata de uma energia mínima, ela está associada ao ponto em que a derivada é zero, certo? Logo, é energia específica da profundidade crítica y c

A profundidade crítica do canal retangular é

y c = Q 2 g b 2 1 / 3

y c = Q 2 9,8 × 20 2 1 / 3 = Q 2 3920 1 / 3

Substituindo na equação da energia para o canal retangular de 20 m de comprimento

E c = y c + Q ² 7840 y c ²

E c = Q 2 3920 1 / 3 + Q ² 7840 Q 2 3920 1 / 3 2

Organizando

E c = Q 2 3920 1 / 3 + Q ² 7840 3920 2 / 3 Q 4 / 3

E c = Q 2 3920 1 / 3 + ( 3920   Q ) 2 / 3 7840

E c = 0,06342   Q 2 / 3 + 0,0 3171   Q 2 / 3

E c = 0,0 9513   Q 2 / 3

Para Q   =   0 m 3 / s → E c = 0   m

Para Q   =   25 m 3 / s → E c = 0 , 813   m

Para Q   =   75 m 3 / s → E c = 1,692   m

Para Q   =   12 5 m 3 / s → E c = 2,378   m

Para Q   =   200 m 3 / s → E c = 3,253   m

E assim, vemos que quanto maior a vazão, maior a energia específica mínima associada ao ponto crítico, conforme esperávamos pelo gráfico.

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #7

Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 774, ex. 11.14

Uma comporta parcialmente aberta em um canal retangular de 5 m de largura carrega água a 10 m³/s. A profundidade a montante é de 2,5 m. Determine a profundidade a jusante e o número de Froude.

Passo 1

Para entender melhor a situação do exercício, vamos ver a figura

Como a comporta está parcialmente aberta isso permite que o escoamento aconteça logo a seguir, e esse é um escoamento em canal aberto, que estamos estudando agora

A profundidade a montante é a profundidade da região 1, onde começa o escoamento. Ou seja, pelo enunciado

y 1 = 2,5   m

O exercício quer saber a profundidade a jusante, ou seja, y 2 e o número de Froude.

Vamos encontrar a profundidade primeiro, utilizando a equação da energia

y 1 + V 1 ² 2 g + p 1 ρ g = y 2 + V 2 ² 2 g + p 2 ρ g + h p

Como não há informações sobre perdas, vamos considerar escoamento sem atrito. Além disso, vamos considerar nas duas regiões a pressão é a mesma (aberto a atmomsfera)

Com isso a equação da energia fica mais simples

y 1 + V 1 ² 2 g = y 2 + V 2 ² 2 g

Lembrando que a velocidade pode ser escrita em função da vazão volumétrica, que foi dada

V = Q A = Q b y

y 1 + Q b y 1 2 2 g = y 2 + Q b y 2 2 2 g

y 1 + Q 2 2 g b y 1 2 = y 2 + Q 2 2 g b y 2 2

Substituindo y 1 , Q e b (do enunciado)

2,5 + 10 2 2 × 9,8 5 × 2,5 2 = y 2 + 10 2 2 × 9,8 5 × y 2 2

Resolvendo

2 , 5327 = y 2 + 0,204 y 2 2

( 2,5327 ) y 2 2 = y 2 3 + 0,204

y 2 3 - 2,5327 y 2 2 + 0,204 = 0

y 2 = 0,302   m

Encontramos a profundidade a jusante!

Passo 2

O número de Froude é

F r = V V o n d a = V g y

Como queremos saber o número de Froude a jusante F r 2

F r 2 = V 2 g y 2

Acabamos de encontrar a profundidade a jusante. Para achar a velocidade, vamos usar V = Q/A novamente

V 2 = Q b y 2

Então Froude é

F r 2 = Q b y 2 1 g y 2

Substituindo

F r 2 = 10 5 × 0,302 1 9,8 × 0,302

F r 2 = 3,85

Resposta

y 2 = 0,302   m

F r 2 = 3,85

Exercício Resolvido #8

Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 774, ex. 11.22

Considere o canal condutor Venturi mostrado. O fundo é horizontal e o escoamento pode ser considerado sem atrito. A profundidade a montante é 0,3 m e a profundidade a jusante é 0,22 m. A largura a montante é 0,6 m e a largura da garganta é 0,3 m. Estime a vazão através do conduto.

Passo 1

E aí! Como o escoamento é sem atrito, vamos usar a equação de Bernoulli (que é a equação da energia sem perdas)

z 1 + V 1 2 2 g + p 1 ρ g = z 2 + V 2 2 2 g + p 2 ρ g

Lembrando que aqui em escoamento aberto trabalhamos com a profundidade y e vamos considerar que nas regiões 1 e 2 temos a mesma pressão (atmosférica)

y 1 + V 1 2 2 g = y 2 + V 2 2 2 g

As velocidades podem ser escritas em função da vazão volumétrica, que é quem queremos calcular

V = Q A = Q b y

Então substituindo na equação da energia

y 1 + Q b 1 y 1 2 2 g = y 2 + Q b 2 y 2 2 2 g

y 1 + Q 2 2 g b 1 y 1 2 = y 2 + Q 2 2 g b 2 y 2 2

Agora podemos substituir os dados e encontrar a vazão Q

0,3 + Q 2 2 × 9,8 0,6 �� 0,3 2 = 0,22 + Q 2 2 × 9,8 0,3 × 0,22 2

Resolvendo

0,08 = Q 2 0,0 8 53 8 - Q 2 0,63504

0,63504 - 0,08538 Q 2 = 0,08 × 0,63504 × 0,08538

Q = 0,089   m 3 / s

Encontramos a vazão volumétrica

Resposta

Q = 0,089   m 3 / s

Exercícios de Livros Relacionados

Um vertedor de soleira delgada retangular com contração final tem 1,5m de comprimento. A que altura deveria a crista do vertedouro ser colocada em um canal para manter uma profundidade a montante de 2
Em uma seção de um canal retangular com 3m de largura, a profundidade é 0,09m para uma descarga de 0,57m 3 / s . Um ressalto suave com 0,03m de altura é colocado sobre o fundo do canal. Determine a va
Considere o canal condutor Venturi mostrado. O fundo é horizontal e o escoamento pode ser considerado sem atrito. A profundidade a montante é 0,3m e a profundidade a jusante é 0,22m . A largura a mont
A figura mostra o escoamento através de uma comporta. Estime a profundidade da água e a velocidade depois da comporta (bem antes do ressalto hidráulico).
Água é descarregada de uma comporta a uma profundidade de 1,25m . A descarga por unidade de largura é 10m 3 / s / m . Estime o nível de água longe a montante onde a velocidade do escoamento é desprezí