Escoamento sob comporta e ressalto hidráulico
Produzido por Raphael EloiTeoria
Escoamento sob comporta
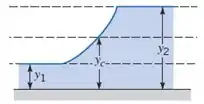
Continuando a falar sobre aquela papo de profundidade crítica e energia mínima: vamos analisar o caso de uma comporta como na imagem abaixo:
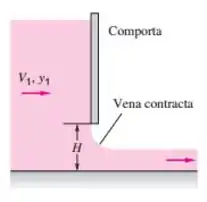
A expressão para o cálcula de é bem simples nesse caso, é como se não houvesse elevação no escoamento.
Em outra palavras tiramos da equação do escoamento sobre elevação:
Esse resultado era obtido quando igualávamos as energias. Ou seja, podemos dizer que se o escoamento a montante (de onde vem o escoamento) é subcrítico, o escoamento à jusante (para onde vai o escoamento) é supercrítico com a mesma energia.
Em outras palavras:
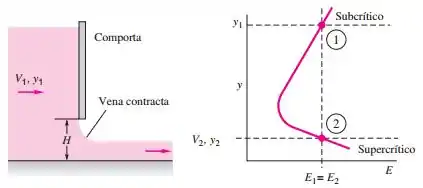
Agora, mais uma informação, ta vendo aquele ? A abertura da comporta.
Podemos escrever a vazão à jusante em função dele:
Sendo a largura do canal, e:
Um fenômeno diferente que podemos ter é o seguinte:
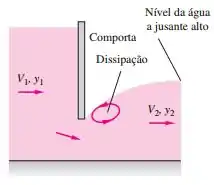
Essa é a representação de uma comporta afogada. Neste caso acontece uma dissipação de energia que chamaremos de ressalto hidráulico, e veremos melhor como funciona adiante.
Ressalto hidráulico
Então esse negócio acontece quando um fluido em estado supercrítico passa pra um estado subcrítico, e isso só pode ocorrer com dissipação de energia. Se liga nessa imagem aqui:
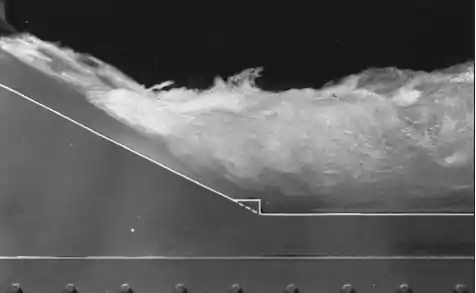
O fluido é rápido e raso a montante e lento e fundo a jusante. O ressalto é exatamente essa camada que você tem as bolhinhas de ar se misturando no fluido.
É nesse movimento confuso que ocorre a perda de energia , para um canal horizontal:
Onde:
Galera, recomendo fortemente dar uma checada em algum vídeo na internet mostrando um ressalto hidráulico, é meio esquisito mesmo.
Vamos praticar então!
Ressalto hidráulico
Exercícios Resolvidos
Exercício Resolvido #1
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Na Figura, seja e . Calcule a vazão por unidade de largura se a energia cinética a montante for (a) desprezada e (b) incluída.
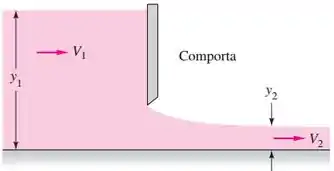
Passo 1
Então galera, neste problema o enunciado nos pede a vazão por unidade de largura, se lembra que a gente chamou isso de quando falamos de profundidade crítica de canais retangulares?
Vou recapitular rapidinho:
Se substituirmos na nossa expressão da energia:
Passo 2
Na letra ele nos pede para desconsiderarmos a energia cinética, que não é nada menos que esse pedaço da equação:
Se desconsideramos, nos deixa com a seguinte expressão:
Logo,
Substituímos e :
Passo 3
Agora, para a lera as coisas são um pouco diferentes, mas bem pouco.
Como não podemos desconsiderar a energia cinética, iremos calcular para depois calcular :
Finalmente,
Substituindo os valores de :
Logo, se :
Resposta
Exercício Resolvido #2
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Na Figura , suponha que e a comporta esteja levantada de maneira que a abertura seja de . Calcule a vazão resultante por unidade de largura e a profundidade a montante.
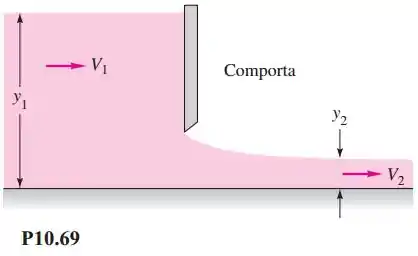
Passo 1
Neste caso como queremos a vazão dada pela abertura da comporta, utilizaremos a expressão:
O enunciado pede para calcularmos a vazão por unidade de largura , o que nos deixa com a expressão:
Passo 2
Calcularemos primeiro
Se e :
Como conhecemos todos os outros valores da expressão de , substituiremos todos para calculá-lo:
Passo 3
Para calcularmos a profundidade a montante, utilizaremos a expressão:
Infelizmente teremos uma equação de terceiro grau, então a solução fica um pouco mais complicada. Existe um fórmula um pouco grande demais pra ser decorada, tipo um Bhaskara, só que de equações de terceiro grau.
Para simplificar as coisas vou usar uma aproximação usando um método numérico bobinho que da pra usar na calculadora, caso você esteja fazendo os exercícios com uma.
Substituindo e :
Se você tem uma calculadora vá colocando valores para na expressão, até que ela convirja para um número próximo de zero, não precisa de muito exato.
É muito improvável que um professor te peça para resolver esse cálculo em alguma prova sem alguma simplificação ou fórmula.
De qualquer maneira a solução converge em
Resposta
Exercício Resolvido #3
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Água escoa em um canal largo a , , e então passa por um ressalto hidráulico. Calcule , o percentual de dissipação e a potência dissipada por unidade de largura. Qual a profundidade crítica?
Passo 1
Então esse exercício é mais intimidador que difícil. Nesse caso é mais organização e entendimento do que a gente viu até agora em canais abertos.
Vamos com calma então.
Calcularemos e a partir dele calcularemos o que o exercício pede.
O bom desse exercício é que ele é meio que um compilado de conceitos.
Passo 2
Utilizaremos a expressão
Utilizaremos isso para calcularmos o número de Froude:
Por que o número de Froude?
Passo 3
Então, neste tópico a gente viu a expressão:
Que nos dá a relação de alturas antes e depois do ressalto hidráulico.
Como já conhecemos :
Substituindo valores:
O que faz sentido já que o ressalto eleva o nível da superfície livre.
Passo 4
Como é constante no escoamento:
Logo o número de Froude é:
Se lembra do que te falei na teoria? De que o ressalto hidráulico é a passagem de um escoamento supercrítico () para um estado subcrítico (). Podemos ver pelos resultado exatamente isso acontecendo.
Passo 5
Finalmente calcularemos as perdas energéticas do ressalto:
Substituindo valores:
Para calcularmos a percentagem de dissipação ou perda, devemos calcular a energia em :
Logo a dissipação foi de :
Resposta
Exercício Resolvido #4
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Para a situação na Figura, considere que na seção 3 a profundidade seja de 2 m e que o número de Froude seja 0,25. Calcule (a) a vazão por metro de largura, (b) , (c), (d) o percentual de dissipação no ressalto hidráulico e (e) a altura da abertura H da comporta.
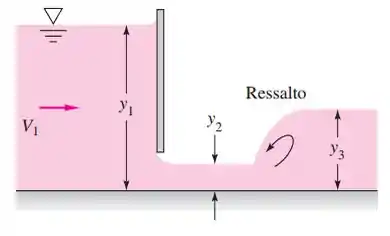
Passo 1
Então time, vamos relacionar os dois temas que vimos nesse tópico: comportas e o ressalto hidráulico.
As coisas são mais conta que difíceis. Vamos calcular as propriedades da cada seção nesta ordem, pois temos valores no enunciado da etapa .
Deveremos então analisar o balanço energético depois do ressalto e ir retornando, fazendo as transições corretas.
Passo 2
Vamos começar calculando a velocidade a partir de e , para encontramos :
Lembrando que :
Passo 3
Para calcularmos a profundidade crítica devemos lembrar do tópico anterior:
Passo 4
Para encontrarmos devemos conhecer as propriedades em , aplciaremos então a teoria de ressaltos hidráulicos:
Esta expressão pode ser reescrita para o caminho contrário, ou seja, calcular de , ao invés de :
Substituindo os valores conhecidos:
Calculamos :
Calcularemos a energia em , que é a mesma que em pois não temos elevação:
Lembramos também da equação da continuidade:
Substituindo uma na outra:
Multiplicando ambos lados por :
Temos uma equação de terceiro grau, com uma única solução positiva:
É um resultado aproximado da solução da equação.
Passo 5
A dissipação no ressalto é
Sabemos que a energia em é:
Logo o percentual de perda é:
Passo 6
E finalmente para calcularmos a abertura da comporta:
Substituiremos na expressão de e substituiremos :
Elevando ambos lados ao quadrado:
Substituido os valores conhecidos:
Resolvendo a equação de segundo grau:
Esta é a única raiz positiva.
Resposta
Exercício Resolvido #5
Concurso Engenheiro Civil – Companhia Docas do RN – CODERN - 2005
O ressalto hidráulico (ou salto hidráulico) consiste na passagem brusca e geralmente turbulenta do regime rápido ou torrencial (regime inferior) para o regime tranqüilo ou fluvial (regime superior), verificando-se
A) aumento da profundidade crítica de escoamento.
B) aumento da profundidade antes do ressalto.
C) manutenção das profundidades de escoamento.
D) aumento da profundidade após o ressalto.
Passo 1
E aí, mestre! Vamos lembrar do que aprendemos sobre ressalto.
O ressalto acontece quando há uma transição brusca do escoamento: de supercrítico para o subcrítico.
A letra A fala da profundidade crítica. Vimos no tópico anterior que a profundidade crítica depende da vazão volumétrica e da geometria do canal aberto.
No ressalto, essas variáveis não mudam, logo, a condição crítica permanece a mesma (nem aumenta nem diminui) e com isso a letra A está errada
Além disso, o ressalto hidráulico acontece justamente porque não há uma forma suave de transição entre o escoamento supercrítico e o crítico, uma vez que as condições antes do ressalto não podem ser alteradas.
Logo, a letra B é incorreta, porque antes do ressalto não há possibilidade de mudança da profundidade :/
A letra C diz que as profundidades se mantém. Bem, se há uma mudança de escoamento supercrítico para subcrítico e ela não pode ser feita a montante (antes) do ressalto, então algo terá que mudar.
No caso, o que muda é a profundidade! O ressalto é um salto do fluido e profundidade aumenta depois dele para realizar essa transição no escoamento. Com isso, a letra C está errada (por dizer que as profundidades se mantém) e a letra D certa, porque a profundidade aumenta com o ressalto.
Resposta
Letra D
Exercício Resolvido #6
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 776, ex. 11.33
Um canal largo carrega 10 m³/s por m de largura a uma profundidade 1 m no pé de um ressalto hidráulico. Determine a profundidade do ressalto e perda de carga através desse.
Passo 1
Primeiro, vamos desenhar o ressalto que acontece nesse escoamento
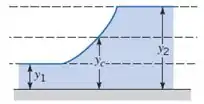
O exercício quer saber a profundidade do ressalto e perda de carga envolvida. Para isso, ele deu a vazão volumétrica por metro de largura do canal, ou seja
Além disso, a profundidade no pé do ressalto é
Para descobrir , vamos usar a relação entre e que vimos na teoria para o ressalto
Conhecemos , mas não ainda o número de Froude do pé do ressalto (em 1). Froude é
Precisamos então achar a velocidade em 1, que é V = Q/A
Como
Substituindo em Froude
Com o número de Froude, vamos conseguir calcular a profundidade do ressalto
Boa! Agora vamos para a perda de carga
Passo 2
No ressalto há perda de energia e ela pode ser escrita da forma de perda de carga
Substituindo a profundidade do ressalto que acabamos de achar :D
A perda de carga através do ressalto é
Resposta
Exercício Resolvido #7
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 776, ex. 11.34
Um ressalto hidráulico ocorre em um canal largo horizontal. A descarga é de 2 m³/s por m de largura. A profundidade a montante é de 750 mm. Determine a profundidade do ressalto
Passo 1
A profundidade do ressalto é o da figura e a profundidade a montante (ou seja, antes) é
Convertendo para o SI
A relação entre (que queremos saber) e (que já conhecemos) no ressalto é
É importante lembrar que podemos usar essa fórmula por se tratar de ressalto, beleza?
Daí, para achar , precisamos encontrar o número de Froude a montante (ou seja na região 1).
Para calcular a velocidade em 1, vamos usar a vazão fornecida, afinal
Mas a vazão fornecida foi a vazão volumétrica por metro de comprimento, ou seja
Então
Substituindo em Froude
Opa! Temos aqui uma questão importante! O Froude antes do ressalto é menor que 1, ou seja, até é um escoamento subcrítico.
Como o ressalto é por definição a transição abrupta de um escoamento supercrítico para um escoamento subcrítico, então não há ressalto! Isso porque inicialmente o nosso escoamento é subcrítico.
Logo, não podemos usar a relação a seguir para encontrar , pois ela só vale para o ressalto
Para obter , utilizaríamos a equação da energia normalmente.
Resposta
Não há ressalto hidráulico
Exercício Resolvido #8
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 775, ex. 11.28
Um canal retangular horizontal com 0,9 m de largura contém uma comporta. A montante da comporta a profundidade é de 1,8 m; a profundidade a jusante é de 0,27 m. Estime a vazão volumétrica no canal
Passo 1
Vamos entender juntos quais são as variáveis fornecidas pelo exercício
Primeiramente, temos um escoamento em canal aberto. A comporta delimita as regiões que vamos analisar. é a profundidade que vem antes (a montante) e é a profundidade que vem depois (a jusante)
Do enunciado, sabemos que
Também sabemos a largura b do canal retangular
Para calcular a vazão, vamos utilizar a equação da energia
No enunciado não há informações sobre perdas, nem sobre ressalto (aliás, nem tem como pois a profundidade diminui da região 1 para a região 2!
Por isso, vamos considerar escoamento sem atrito. Outro ponto é que as pressões se cancelam pois são a atmosférica. A equação da energia atualizada para esse caso é
Queremos encontrar a vazão, por isso, vamos escrever as velocidades em função dela 😉 Lembrando que a área é a do retângulo, porque essa é a geometria do canal
Substituindo na equação da energia
Estamos prontos para substituir os dados para encontrar Q :D
Encontramos a vazão volumétrica!