Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 5.Problemas Abrangentes - Ex. 5

A antena do rádio de um automóvel vibra em ressonância devido à emissão de vórtices? Considere uma antena de comprimento L e diâmetro D. De acordo com a teoria da vibração de vigas (veja Kelly [34], p. 401), a frequência natural do primeiro modo de vibração de uma viga circular sólida em balanço é vn 5 3,516[EI/(rAL4)]1/2, em que E é o módulo de elasticidade, I é o momento de inércia de área, r é a massa específica do material da viga e A é a área da seção transversal da viga.

(a) Mostre que vn é proporcional ao raio R da antena. (b) Se a antena for de aço, com

L = 60 cm e D = 4 mm, estime a frequência de vibração natural em Hz. (c) Compare com a frequência de emissão se o carro se move a 105 km/h.

Passo 1

E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!

Nesse problema, temos uma antena de um automóvel que vibra em ressonância devido à emissão de vórtices.

Para modelar esse problema, o enunciado forneceu a senguinte equação para a frequência natural de vibração de uma viga circular sólida em balanço:

ω n = 3,516 E I ρ A L 4 1 / 2

Sendo E o módulo de elasticidade, I o momento de inécia da seção circular, A a área da seção circular e L o comprimento da antena.

O enunciado nos pede para mostrar que ω n é proporcional ao raio da antena, além de estimar a vibração natural em H z para L = 60   c m e D   =   4   m m e também comparar a frequência com a frequência de emissão se o carro se move a 105   k m / h .

Vem comigo pra gente resolver essa questão juntos!

Passo 2

Em primeiro lugar, vamos resolver a letra (a).

Olhando pra equação de ω n apresentada no passo um, podemos expandir a área como uma função do raio dada por A = π R ² e o momento de inércia da área como sendo I = 1 4 π R 4 .

Substituindo, nós vamos ficar com:

ω n = 3,516 E π R 4 / 4 ρ π R ² L 4 1 / 2

ω n = 1,758 E ρ R L ²

Como dá pra gente perceber, a frequência natural de vibração é diretamente proporcional ao raio d antena R .

Passo 3

Agora, vamo responder a letra (b).

Agora, devemos calcular ω n para uma antena de aço com L = 0,6   m e R = D 2 =   0,002   m .

Para o aço, o módulo de elasticidade é E   =   2 , 1 × 10 11   P a e a massa específica ρ =   7840   k g / m ³ .

Substituindo na equação que deduzimos no passo anterior:

ω n = 1,758   2 , 1 × 10 11   P a   7840   k g / m ³   0,002   m 0,6   m ² = 50,5   r a d / s

Considerando que 1   r a d / s equivale a 0 , 159   H z , o valor de ω n será:

ω n = 8,04   H z

Passo 4

Pra finalizar a questão, vamo responder a letra (c).

Vamos calcular o número de Reynolds para o carro se movendo a v = 105 k m h = 29,2 m s . Consideramos a massa específica do ar como ρ a r = 1,2   k g / m ³ e sua viscosidade como μ = 1,8 × 10 - 5   P a . s .

Logo, teremos:

R e = ρ v D μ = 1,2   k g / m ³   29,2   m / s 0,004   m 1,8 × 10 - 5   P a . s = 7787

Agora iremos relacionar o número de Reynolds encontrado com o chamado número de Strouhal, que relaciona a frequência emitida por vórtices com a velocidade de um fluido:

S t = ω e m i s s ã o D v

Olhando o gráfico da página 322, podemos ver que para o valor de Reynolds que encontramos S t   ≅ 0,21 :

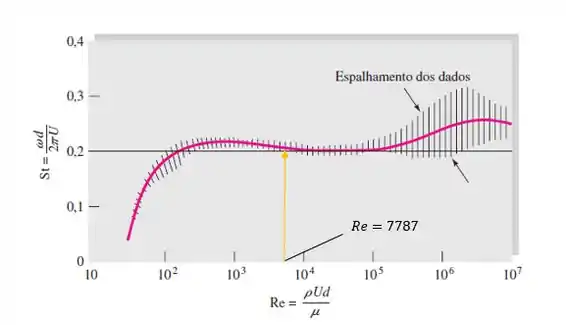
Agora podemos calcular o valor de w e m i s s ã o :

ω e m i s s ã o ( 0,004   m ) 29,2   m / s = 0,21

ω e m i s s ã o = 1533   H z

Ou seja, a frequência de emissão ω e m i s s ã o é muito maior que a frequência natural ω n .

Resposta

(a) A frequência natural de vibração é diretamente proporcional ao raio d antena R , ω n = 1,758 E ρ R L ²

(b) A frequência de vibração natural é ω n = 8,04   H z

(c) A frequência de emissão se o carro se move a 105   k m / h é ω e m i s s ã o = 1533   H z

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Escreva as dimensões primárias da constante universal dos gases ideais, R u . (Sugestão: use a lei dos gases ideais, P V = n R u T , onde P é pressão, V é o volume, T é a temperatura absoluta e n é o
Em uma tabela periódica dos elementos, a massa molar M , também chamada p e s oa t ô m i c o ô , quase sempre é listada como se fosse uma quantidade adimensional (Figura P7-5). Na verdade, o p e s oa
Escreva as dimensões primárias de cada uma das seguintes variáveis do estudo da transferência de calor por convecção (Figura P7-16), mostrando todo o seu trabalho: a taxa de geração de calor g ˙ . (Di
A condutividade térmica k é uma medida da capacidade de um material de conduzir calor (Figura P7-15). Para a transferência de calor na direção x , através de uma superfície normal à direção x , a lei
Definimos a c o n s t a n t ee s p e c í f i c ad og á si d e a lR g á s í á á para um determinado gás como a relação entre a constante universal dos gases e a massa molar (também chamada p e s om o l