Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 1.Exercício - Ex. 14

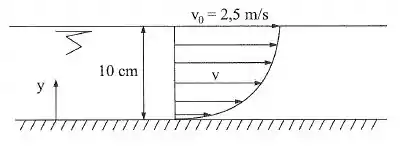
Assumindo o diagrama de velocidades indicado na figura, em que a parábola tem seu vértice a 10   c m do fundo, calcular o gradiente de velocidade e a tensão de cisalhamento para y = 0 ; 5 ; 10   c m . Adotar μ = 400   c e n t i p o i s e s .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

A nossa estratégia para resolver esta questão é encontrar uma equação para a velocidade que expresse o comportamento do sistema para que possamos substituir cada ponto solicitado.

Como o sistema representa uma parábola, podemos então representar a equação da velocidade como:

v = a y 2 + b y + c

Onde a , b e c são constantes a serem descobertas.

Passo 2

Da figura do enunciado, sabemos que para y = 10   c m = 0,1   m , temos que v = v 0 = 2,5   m / s . Portanto:

2,5 = a 0,1 2 + b 0,1 + c

Temos também a condição em que para y = 0 , v = 0 , logo:

0 = a 0 2 + b 0 + c

c = 0

Sabemos que, para y = 0,1   m , o gradiente de velocidade é nulo, logo:

d v d y = 0

Derivando a equação da velocidade, temos que:

d v d y = 2 a y + b

Aplicando a condição, temos que:

0 = 2 a 0,1 + b

b = - 0,2 a

Substituindo na primeira relação encontrada, temos que:

2,5 = a 0,1 2 + ( - 0,2 a ) 0,1 + 0

a = - 250

Logo:

b = - 0,2 - 250

b = 50

Passo 3

A nossa equação da velocidade será:

v = - 250 y 2 + 50 y

E:

d v d y = - 500 y + 50

Como queremos o gradiente nos pontos solicitados, temos que:

P a r a   y = 0 → d v d y = - 500 0 + 50

P a r a   y = 0 → d v d y = 50

Temos também que:

P a r a   y = 0 , 05 → d v d y = - 500 0 , 05 + 50

P a r a   y = 0 , 05 → d v d y = 25

E:

P a r a   y = 0 , 1 → d v d y = - 500 0 , 1 + 50

P a r a   y = 0 , 1 → d v d y = 0

Passo 4

Também queremos as tensões de cisalhamento relacionadas à estes gradientes. Sabendo que:

τ = μ d v d y

Temos que:

P a r a   y = 0 → τ = 400 × 10 - 2 50

P a r a   y = 0 → τ = 200 d i n a c m 2

Temos também que:

P a r a   y = 0 , 05 → τ = 400 × 10 - 2 25

P a r a   y = 0 , 05 → τ = 1 00 d i n a c m 2

E:

P a r a   y = 0 , 1 → τ = 400 × 10 - 2 0

P a r a   y = 0 , 1 → τ = 0

Resposta

P a r a   y = 0 → d v d y = 50

P a r a   y = 0 → τ = 200 d i n a c m 2

P a r a   y = 0,05 → d v d y = 25

P a r a   y = 0,05 → τ = 100 d i n a c m 2

P a r a   y = 0,1 → d v d y = 0

P a r a   y = 0,1 → τ = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As linhas de emissão são visualizadas por meio de um fluido corante de empuxo neutro injetado em um campo de escoamento a partir de um ponto fixo no espaço. Uma partícula do fluido corante que está no
Um escoamento é descrito pelo campo de velocidade V =a x i+b j , em que a=1 / 5s- 1 b=1m / s . As coordenadas são medidas em metros. Obtenha uma equação para a linha de corrente que passa através do p
Um escoamento é descrito pelo campo de velocidade V =a y i+b t j , em que a=0,2s - 1 e b=0,4 m / s 2 . Em t=2s , quais são as coordenadas da partícula que passou pelo ponto (1, 2) em t = 0. Em t=3s ,
Um escoamento é descrito pelo campo de velocidade V =a i+b x j , em que a=2m / s e b=1s- 1 . As coordenadas são medidas em metros. Obtenha a equação para a linha de corrente que passa pelo ponto ( 2 ,
Um campo de velocidade é dado por V → = a x t î-b y j ^ î , em que a=0,1s - 2 e b=1s - 1 . Para a partícula que passa pelo do ponto ( x ,y )=( 1 ,1 ) no instante t=0s , trace a trajetória durante o in