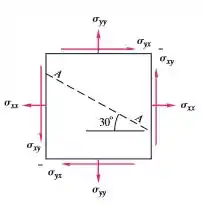
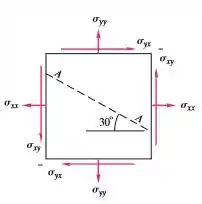
Exercícios de Tensão cisalhante e tipos de fluidos - Lista de Exercícios Resolvida
Questão 1
Considere o gráfico de Tensão Cisalhante por taxa de deformação (taxa de cisalhamento) a seguir:
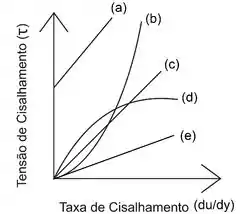
Cada curva representa um fluido diferente. Qual(is) dos fluidos são newtonianos? Por quê?
Ver solução completaQuestão 2
Em relação ao comportamento reológico de fluidos, analise as proposições a seguir.
A viscosidade de um fluido sempre diminui com o aumento da temperatura.
Fluidos nos quais a tensão de cisalhamento não é proporcional ao quadrado da taxa de deformação são ditos fluidos não newtonianos.
Um fluido plástico de Bingham não escoa quando submetido a uma tensão de cisalhamento inferior a um determinado valor limite.
Há fluidos não newtonianos nos quais a viscosidade aparente varia com o tempo.
São corretas APENAS as proposições
Ver solução completa
Questão 3
(Adaptada) A distribuição de velocidade para o escoamento laminar desenvolvido entre placas paralelas é dada por
em que é a distância separando as placas e a origem está situada na linha mediana entre as placas. Considere um escoamento de água a 20°C, com e . Calcule a tensão de cisalhamento na placa superior e dê o seu sentido.
Ver solução completaQuestão 4
(Adaptada) Entre duas placas paralelas de área cada, estão contidos dois fluidos imiscíveis com viscosidades e conforme mostra a figura. As espessuras das camadas de líquido são e , respectivamente. a) Determine a força para fazer com que a placa superior se mova a uma velocidade de . b) Qual é a velocidade do fluido na interface entre os dois fluidos?
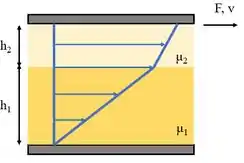
Questão 5
(Adaptada) O perfil de velocidade de um fluido que escoa sobre uma superfície é definido por:
Sabe-se que o fluido é água a 20°C e que é a espessura do escoamento. Sendo , encontre a expressão para taxa de deformação .
Ver solução completaQuestão 6
A distribuição de velocidade para o escoamento laminar desenvolvido entre placas paralelas é dada por
em que é a distância separando as duas placas; a origem está situada na linha mediana entre as placas. Considere o escoamento de água a 20°C com velocidade máxima de e . Calcule a força sobre uma seção de 1m² da placa inferior e dê o seu sentido.
Ver solução completa