Em um campo de escoamento incompressível oscilante, a força por unidade de massa que age sobre uma partícula é obtida da Segunda Lei de Newton na forma intensiva (consulte o Problema 7-20),

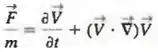
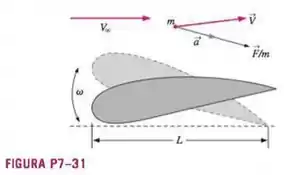
Suponhamos que a velocidade e o comprimento característicos de determinado campo de escoamento sejam , respectivamente. Suponhamos também que seja uma frequência angular característica (rad/s) da oscilação (Figura P7-31). Defina as seguintes variáveis adimensionalizadas,

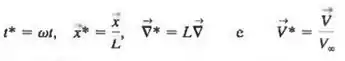
Como não foi dada nenhuma escala característica para a força por unidade de massa que age na partícula de fluido, nós escolhemos uma observando que . Ou seja, tomamos

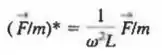
Adimensionalize a equação do movimento e identifique todos os parâmetros adimensionais usuais (nomeados) que possam aparecer.

Para reescrever a Eq. 1 adimensionalizada, nós podemos substituir as variáveis ​​não dimensionadas da equação, que já sabemos as relações, dadas no problema.

Ficou confuso?

Por exemplo, pelas variáveis definidas no enunciado, temos que e .

Assim, substituindo as variáveis ​​não dimensionadas da equação:

Podemos simplificar multiplicando cada termo por :

Reconhecemos o parâmetro adimensional entre parênteses na Eq. 2 como (número Strouhal). Assim, reescrevemos a Eq. 2 como:

P.s: Usamos a frequência angular ω nesse problema. O mesmo resultado seria obtido se usássemos a frequência. A equação 2 é a base para formar a equação diferencial para conservação do momento linear de um campo de fluxo instável e incompressível.