Enunciado
Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 79
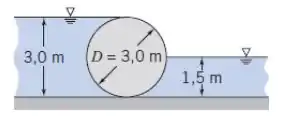
Considere a barragem cilíndrica com diâmetro de 3 m e comprimento de 6 m. Se o fluido no lado esquerdo tem SG = 1,6 e o fluido no lado direito tem SG = 0,8, determine o módulo e o sentido da força resultante.
Passo 1
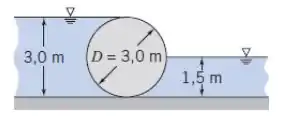
Nesse problema temos uma esfera com diferentes fluidos de cada lado. Devemos encontrar a força e direção resultantes.
Mas para a resolução notamos que as forças são tratadas em partes, em que para cada um, a força horizontal é equivalente à em uma placa plana vertical, já a força vertical é equivalente ao peso do fluido.
Para forças horizontais, a equação é . E para forças verticais, a equação é .
Passo 2
Calculando para as forças horizontais, temos:
Para o fluido 2:
Portanto, a resultante da força horizontal é: .
Passo 3
Para a geometria esquerda, é necessário um experimento para obter superfícies com fluido, a seguir:
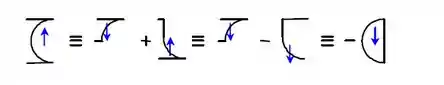
Para o lado direito, usando uma lógica semelhante:
Portanto, a resultante da força horizontal é: .
Finalmente, a força e a direção resultantes podem ser calculadas:
Prontinho!!