Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 116
As correntes oceânicas podem ser rastreadas por flutuadores Swallow [2], que receberam esse nome em homenagem ao Dr. John Swallow, do Reino Unido, que os projetou em 1955. Houve muitas alterações no projeto, mas o flutuador original era um tubo de alumínio, com 6 cm de diâmetro externo e aproximadamente 3 m de comprimento, selado em ambas as extremidades e levemente pressurizado. Os tubos tinham de ser corroídos para obter a espessura correta. Calcule a espessura do tubo para obter a flutuabilidade neutra na água do mar com massa específica de 1.030 kg/m3.
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
A primeira ideia que a gente tem que ter da questão é de qual assunto ela faz parte. Esse problema em específico é referente à seção 2.8 do livro, chamada “Empuxo; princípios de Arquimedes”.
Nessa problema, temos um cilindro de alumínio raio externo e de comprimento, preenchido com ar do lado interno, imerso na água do mar.
Pra mentalizar melhor o problema, dá uma olhadinha na figura abaixo:
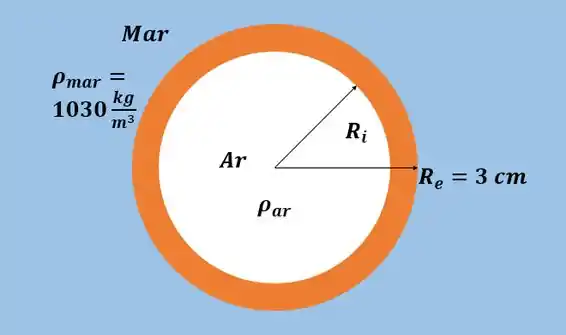
O enunciado pede que a gente descubra a espessura do tubo para que ele obtenha flutuabilidade neutra.na água do mar, de massa específica .
Pra resolver a questão, devemos lembrar que, para um corpo com flutuabilidade neutra, o empuxo será igual ao peso do corpo. No caso do nosso problema, o empuxo deve ser igual ao peso da casca cilíndrica de alumínio mais o peso do ar na parte interna do tubo:
Nos próximos passos, eu vou te ensinar como calcular os pesos e o empuxo, e também a como encontrar o raio interno e, a partir dele, achar a espessura do tubo.
Vem comigo pra resolver a questão!
Passo 2
Para calcular o empuxo, basta que a gente multiplique o peso específico do fluido, que aqui é a água do mar, pelo volume de fluido deslocado. Como estamos considerando a flutuabilidade neutra, o volume deslocado será igual ao volume externo do cilindro:
Sendo: a aceleração da gravidade; e o comprimento do cilindro.
Da mesma forma, o peso da casca cilíndrica do alumínio pode ser calculado como:
Sendo: a massa específica do alumínio a temperatura ambiente; e a área da região anular do tubo.
E, ainda, a gente pode definir a força peso do ar dentro da parte interna do cilindro como:
Sendo a massa específica do ar. O enunciado do problema não afirma qual a densidade do ar, mas afirma que ele está levemente pressurizado. Dessa forma, consideramos .
Substituindo essas três relações na equação que definimos no Passo 1, teremos:
Notem que , e podem ser cortados, pois se repetem em todos os termos:
Passo 3
Pra finalizar a questão, vamo substituir todas as grandezas que conhecemos na equação definida no fim do Passo 2:
Ou seja, a espessura do tubo é
Pronto, matamos a questão juntos!
Resposta
A espessura do tubo é