Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 8.Exercício - Ex. 9

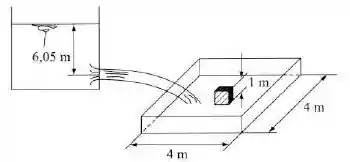
No fundo do reservatório inferior da figura, inicialmente vazio, situa-se um cubo de madeira de 1 m de aresta. Do reservatório superior escoa água através de um orifício de aresta viva, cujo coeficiente de contração é C c = 0,6 . Determinar o valor do coeficiente de velocidade do orifício, para que o corpo comece a flutuar em 20 s. Dados: γ m a d e i r a = 8000   N / m 3 ; A o r i f í c i o = 0,1   m 2 ; g = 10   m / s 2 .

Passo 1

Nesse exercício, teremos E = G , sendo:

E = γ H 2 O V s u b

G = γ m a d V c u b o

Vamos começar calculando G , pois já temos todos os dados necessários:

G = γ m a d V c u b o = 8000 1 3 → G = 8000   N

Agora, igualando esse valor na equação para o empuxo, temos:

E = γ H 2 O V s u b = 8000 → γ H 2 O A b a s e h s u b = 8000

Substituindo os valores dados no enunciado, temos:

10000 1 2 h s u b = 8000 → h s u b = 0,8   m

Passo 2

Dessa forma, o volume total no reservatório será:

V = A b a s e h s u b = 4 4 0,8 → V = 12,8   m 3

Agora podemos encontrar a vazão necessária para que o corpo comece a flutuar no intervalo de tempo de 20 s:

Q = V t = 12,8 20 → Q = 0,64   m 3 / s

Passo 3

Sabemos que a velocidade teórica de saída de um reservatório de altura h pode ser dada pela equação 8.8 apresentada nessa seção:

v t = 2 g h = 2 ( 10 ) ( 6,05 ) → v t = 11   m / s

Agora podemos calcular a vazão teórica:

Q t = v t A o = 11 0,1 → Q t = 1,1   m 3 / s

E, com isso, agora calcular o coeficiente de descarga C D :

C D = Q r Q t = 0,64 1,1 → C D = 0,582

E, finalmente, podemos encontrar o coeficiente de velocidade através da relação apresentada no livro, dada por:

C D = C v C c → C v = C D C c = 0,582 0,6 → C v = 0,97

Resposta

C v = 0,97

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o escoamento de água a 20°C na figura abaixo, use a combinação de tubo de Pitot e tomada de pressão estática para calcular (a) a velocidade na linha de centro e (b) a vazão volumétrica no tubo li
Uma solução precisa do problema P6.143, usando a figura abaixo, requer iteração porque tanto a ordenada como a abcissa dessa figura contêm a vazão Q, que é incógnita. No espírito do exemplo 5.11, enco
Um pesquisador precisa medir a velocidade do escoamento momento em um túnel de água. Devido às restrições orçamentárias, ele não dispõe de um tubo de Pitot estático, mas, em vez disso, insere uma sond
Um tubo liso contém etanol a 20°C escoando a 7 m³/h por uma obstrução de Bernoulli, como na figura abaixo. São instalados três tubos piezométricos, como mostrado também. Se a obstrução é uma placa de
Um engenheiro que curso mecânica dos fluidos na faculdade sem fundamentos sólidos colocou uma tomada de pressão estática a montante e longe da sonda de estagnação, como mostra na figura abaixo, compro