Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 6º - Capítulo 4.Problemas - Ex. 76
Um grande problema na montagem de circuitos integrados em grande escala (VLSI- very large-scale integrated) é o resfriamento de seus elementos. O problema resulta do aumento no nível de dissipação de potência do interior do chip, bem como da montagem mais compacta dos chips em um módulo. Uma nova técnica para o resfriamento de módulos contendo vários chips foi desenvolvida pela IBM. Denominada módulo de condução térmica (TCM -thermal conduction module), os chips são soldados a um substrato cerâmico de múltiplas camadas e o calor dissipado em cada chip é conduzido através de um pistão de alumínio, pressionado sobre o chip por uma mola, para uma placa fria que é resfriada com água.
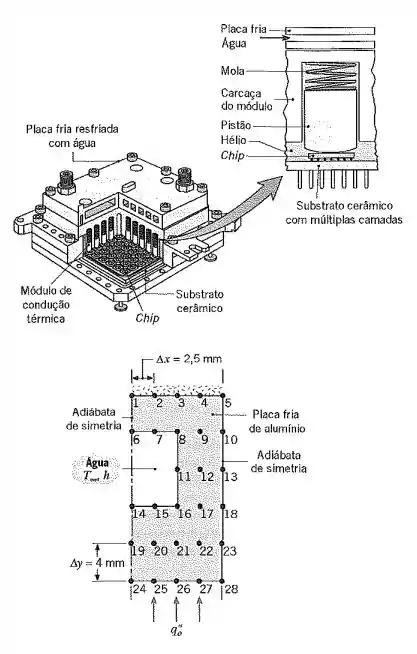
(a) Seja uma placa fria feita de alumínio ( k = 190 W/(m- K)) com canais retangulares, regularmente espaçados, através dos quais escoa água. Sob condições normais de operação, a dissipação de potência no interior dos chips resulta em um fluxo térmico uniforme de q"0 — 105 W/m2 na base da placa fria, enquanto a água disponibiliza uma temperatura T„— 15°C, com um coeficiente de transferência de calor por convecção h — 5000 W/(m2 - K) no interior dos canais. Estamos interessados em obter a distribuição de temperaturas, em regime estacionário, no interior da placa fria e, por questões de simetria, podemos concentrar nossa atenção na rede nodal mostrada na figura. Supondo que a superfície superior da placa fria esteja isolada, determine as temperaturas nodais.
(b) Embora exista o interesse de operar em níveis de potência mais elevados, considerações a respeito da confiabilidade do sistema exigem que a temperatura máxima na placa fria não seja superior a 40°C. Usando a geometria da placa fria e a rede nodal especificadas na figura, avalie o efeito de mudanças nas condições de operação ou de projeto com o objetivo de aumentar o fluxo térmico operacional q"0 . Estime o limite superior para o fluxo térmico.
Passo 1
Fala aí galerinha? Tudo bem com vocês? Bora pra cima! Saca só esse esquemático dividindo a peça em várias regiões:
As equações de diferenças finitas devem ser obtidas para cada um dos 28 nós. Aplicando o método do balanço de energia às regiões 1 e 5, que são semelhantes, segue-se que para os nós 1 e 2, respectivamente:
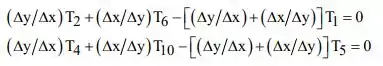
As regiões nodais 2, 3 e 4 são semelhantes, e o método do balanço de energia produz uma equação de diferenças finitas da forma
Balanços de energia aplicados às combinações remanescentes de nós semelhantes produzem as seguintes equações de diferenças finitas.
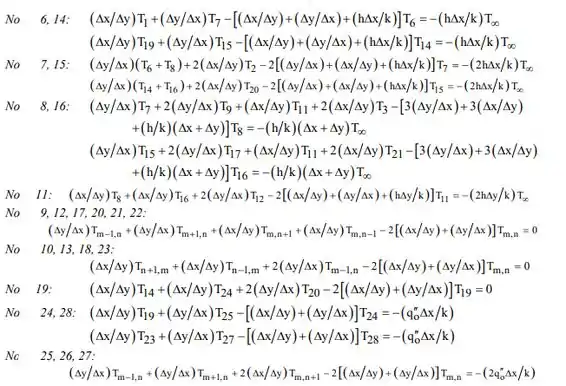
Passo 2
Avaliando os coeficientes e resolvendo as equações simultaneamente, a distribuição de temperatura em estado estacionário (°C), tabulada de acordo com as localizações dos nós, é:
Alternativamente, os resultados anteriores podem ser facilmente obtidos acessando o painel IHT Tools e usando as opções 2-D, SS, equações diferenciais finitas, as equações do modelo estão anexadas). As temperaturas máxima e mínima da placa fria estão nos locais inferior (T24) e superior central (T1), respectivamente.
(b) Para as condições prescritas, a temperatura máxima permitida (T24 = 40°C) é atingida quando o
As opções para estender esse limite podem incluir o uso de uma placa fria de cobre (k ≈ 400 W/m⋅K) e/ou aumentar o coeficiente de convecção associado ao refrigerante. Com
, um valor de pode ser mantido.
Com
(um limite superior prático), q′′o = 28,65 W/cm2.
Melhorias adicionais, embora pequenas, podem ser realizadas realocando os canais de refrigeração mais perto da base da placa fria.
Resposta
Resposta nos passos