Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 21

Modifique o problema P3.16 da seguinte maneira: Considere que a placa tenha comprimento L = 125 δ da entrada até a saída. A placa é porosa e está retirando fluido da camada-limite a uma velocidade de sucção uniforme v w . (a) Calcule Q através da superfície superior se v w = 0,002 U o . (b) Encontre a razão v w / U o para qual Q através da superfície superior é zero.

Passo 1

E aí, tranquilo?? Vamos para mais um lerigou da mecflu? LERIGOU!

Primeiro, vamos relembrar o problema P3.16?

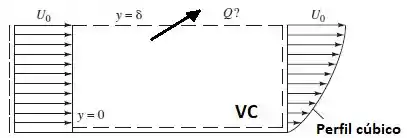
Perfil cúbico: u ≈ U o 3 η - η 3 2 onde η = y / δ

Agora temos também uma vazão de saída pela parte inferior da placa, ou seja, temos algo assim ó:

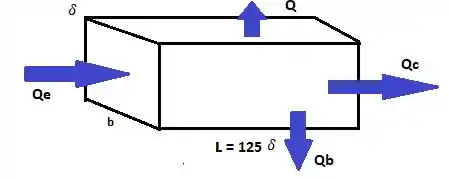
Passo 2

(a) Pelo balanço de massa vamos ter que:

Q e = Q + Q b + Q c

As áreas transversais de escoamento de Q e e Q c são iguais do problema P3.16, então podemos usar os valores encontrados nele, beleza?

Lembrando sempre que: A vazão volumétrica é dada pela velocidade média multiplicada pela área transversal de escoamento. Quando tivermos um valor constante de velocidade, basta multiplicarmos essa velocidade com a área transversal. Caso haja um PERFIL, precisamos integrar o perfil na área, beleza?

Q e = U 0 δ b

Q c = ∫ 0 b ∫ 0 y U 0 3 y 2 δ - y 3 2 δ 3 d x d y

Q c = U 0 b 5 8 δ

Q b = 0,002 U 0 125 δ b = 0,25 U 0 δ b

Passo 3

Pelo balanço então, calculamos que Q = Q e - ( Q b + Q c )

Q = U 0 δ b - 0,25 U 0 δ b + 5 8 U 0 b δ

Q = U 0 δ b - 2 U 0 δ b + 5 U 0 b δ 8

Q = U 0 δ b 1 - 2 + 5 8 = U 0 δ b 1 - 7 8 = 1 8 U 0 δ b

Passo 4

(b) Considerando que Q = 0

Q = Q e - ( Q b + Q c )

Q e = Q b + Q c

U 0 δ b = v w 125 δ b + 5 8 U 0 b δ

U 0 δ b - 5 8 U 0 b δ = 125 δ b v w

U 0 δ b - 5 8 δ b = 125 δ b v w

v w U 0 = δ b - 5 8 δ b 125 δ b = δ b - 5 8 δ b 125 δ b δ b δ b = δ 2 b 2 - 5 8 125 δ 2 b 2   = δ 2 b 2 125 δ 2 b 2 - 5 125 δ 2 b 2 8

v w U 0 = 1 125 - 1 200 δ 2 b 2

v w U 0 = 0,008 - 0,005 δ 2 b 2

Resposta

  1. 1 8 U 0 δ b
  2. v w U 0 = 0,008 - 0,005 δ 2 b 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água escoando por um tubo com 8 c m de diâmetro entra em uma seção porosa, como mostra a figura P3.10, que permite uma velocidade radial uniforme v w através das superfícies das paredes por uma distân
Um tanque de teste de laboratório contem água do mar com salinidade S e massa específica ρ . Água entra no tanque nas condições ( S 1 ; ρ 1 ; A 1 ; V 1 ) e, por hipótese, mistura-se imediatamente no t
O escoamento no tubo na Figura P 3.12 enche um tanque de armazenagem cilíndrico conforme mostrado. No tempo t = 0 , a profundidade da água no tanque é 30c m . Calcule o tempo necessário para encher o
O recipiente cilíndrico da Figura P 3.13 tem 20c m de diâmetro e uma contração cônica no fundo com um furo de saída de3c m de diâmetro. O tanque contém água limpa nas condições padrão ao nível do mar.
O tanque aberto da Figura P 3.14 contém água a 20 ° C e está sendo enchido através da seção 1 . Considere o escoamento incompressível. Primeiro, deduza uma expressão analítica para a taxa de variação