A passagem de uma corrente elétrica através de um longo bastão condutor, de raio e condutividade térmica , resulta em um aquecimento volumétrico uniforme a uma taxa . O bastão condutor é coberto por um revestimento de material não condutor elétrico, com raio externo e condutividade térmica . A superfície externa é resfriada por convecção por um fluido.
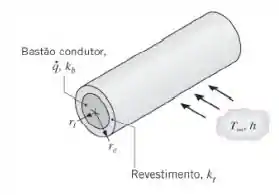
Para condições de regime estacionário, escreva formas apropriadas da equação do calor para o bastão e para o revestimento. Escreva também as condições de contorno apropriadas para a solução dessas equações.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado quer que a gente determine diferentes formas da gente escrever a equação do calor para o bastão e para o revestimento. Além disso, nós precisamos saber quais são as nossas condições de contorno.
Nós temos um bastão condutor que é revestido por um material não condutor e a superfície externa é resfriada por convecção em um fluido:
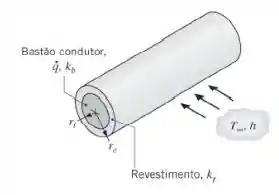
Esse problema envolve duas regiões distintas: o bastão condutor (região interna) e o revestimento (região externa), ambas em coordenadas cilíndricas.
Então, o que nós vamos fazer é determinar a equação do calor em coordenadas cilíndricas, considerando a região de condução do bastão () e considerando a região do revestimento ().
Vamos nessa!
Passo 2
Bom, vamos começar escrevendo nossa equação da transferência de calor para o bastão.
A forma geral da equação do calor em regime estacionário, unidimensional (assumindo simetria radial e bastão longo ) com geração de calor interna é:
Na região do bastão condutor, temos . O bastão condutor possui condutividade térmica e geração de calor volumétrica uniforme . Então, a equação do calor vai ficar:
Simplificando (assumindo constante), temos:
Devido à simetria geométrica e térmica no centro do bastão, o gradiente de temperatura deve ser zero. Então, nossa primeira condição de contorno (), para o centro do bastão, é:
A temperatura do bastão deve ser igual à temperatura do revestimento na interface. Então, a segunda condição de contorno (), para a interface e a continuidade de temperatura, é:
Passo 3
Agora vamos formular a equação para o revestimento ().
O revestimento possui condutividade térmica e não tem geração de calor interna ( ). Então, nossa equação do calor vai ficar:
Simplificando (assumindo constante), temos:
A condição de contorno () é para a interface e a continuidade do fluxo de calor. O fluxo de calor por condução que sai do bastão deve ser igual ao fluxo de calor por condução que entra no revestimento. Então, temos:
E a quarta condição de contorno () é a para a superfície externa e a condição de convecção. O fluxo de calor por condução que chega à superfície externa do revestimento é igual ao fluxo de calor transferido por convecção para o fluido externo . Assim, temos:
Uhul! Conseguimos!
Valeu, galera! Até a próxima! 😉