Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 21

Repita o Exemplo 9–1 (gás comprimido em um cilindro por um pistão), mas sem usar a equação de continuidade. Em vez disso, considere a definição fundamental de densidade como massa dividida por volume. Verifique se a Eq. 5 do Exemplo 9–1 está correta.

Passo 1

Faaaaala galerinhaa!!

Animados para seguir?

Vamos dar uma olhada na ilustração do Exemplo 9.1:

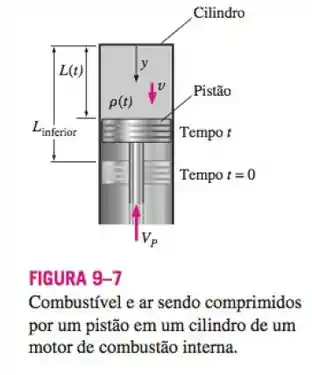
Vamos assumir aqui que a densidade é uniforme ao longo do cilindro em um dado instante, mas ela vai mudar com o tempo, ok?

Também vamos assumir que não há nenhuma massa “fugindo” do cilindro enquanto ele é comprimido!

Beleza!

Agora vamos calcular o volume inicial do cilindro, neste caso a altura será igual à distância L i n f e r i o r e a área da seção transversal, A:

V 0 = L i n f e r i o r A

E após certo tempo:

V t = L t A

O exemplo nos disse que depois de um tempo t o novo comprimento seria dado por:

L t = L i n f e r i o r - V p t

Onde V p é a velocidade constante com que o cilindro sobe!

Portanto:

V t = L i n f e r i o r - V p t A

Passo 2

Se já achamos o volume, achar a massa é moleza, certo?

Basta lembrarmos que ela se relaciona com a densidade naquele instante:

m = ρ ( 0 ) V 0

m = ρ ( 0 ) L i n f e r i o r A

E no tempo t:

m = ρ ( t ) V t

m = ρ ( t ) L i n f e r i o r - V p t A

Como a massa não vai se alterar:

ρ 0 L i n f e r i o r A = ρ ( t ) L i n f e r i o r - V p t A

ρ 0 L i n f e r i o r = ρ ( t ) L i n f e r i o r - V p t

Reorganizando:

ρ ρ ( 0 ) = L i n f e r i o r L i n f e r i o r - V p t

Simplificamos o termo à direita por L i n f e r i o r :

ρ ρ ( 0 ) = 1 1 - V p t L i n f e r i o r

Se quisermos transformar esta equação para obter resultados adimensionais, como no Exemplo 9.1:

ρ ρ ( 0 ) = ρ *

V p t L i n f e r i o r = t *

Então:

ρ * = 1 1 - t *

Exatamente igual ao que obtivemos no Exemplo, certo?

Chegamos a conclusão que a Eq. 5 do Exemplo 9–1 está correta !!

Resposta

A   E q .   5   d o   E x e m p l o   9 – 1   e s t á   c o r r e t a   ‼

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o escoamento em torno de um cilindro circular com velocidade de corrente livre da direita para a esquerda e um vórtice livre de sentido anti­horário. Mostre que a força de sustentação sobre
Um modelo grosseiro de um tornado é formado pela combinação de um sorvedouro, de intensidade q = 2800m 2 / s , e um vórtice livre, de intensidade K = 5600m 2 / s . Obtenha a função de corrente e o pot
Considere o escoamento sobre um cilindro circular de raio a , como no Exemplo 6.11. Mostre que V r = 0 ao longo das linhas ( r , θ ) = r , ± π 2 . Trace um gráfico de V θ U versus o raio para r ≤ a ,
Uma fonte e um sorvedouro com intensidades de igual magnitude, q = 3 πm 2 / s , são colocados sobre o eixo x em x = - a e x = a , respectivamente. Um escoamento uniforme, com velocidade U = 20 m / s n
Considere novamente o escoamento sobre um corpo de Rankine do Problema 6.122. A meia ­largura, h , do corpo na direção y é dada pela equação transcendente h a = c o t π U h q Avalie a meia ­largura, h