Cavitação em bombas
Produzido por Raphael EloiTeoria
Introdução
Fala, mestre! Você já ouviu falar em cavitação de bombas? Bora entender juntos que parada é essa!
A cavitação é basicamente quando a energia de pressão do fluido se transforma em energia térmica, ou seja, o fluido “perde pressão” e gera calor.
Quando a pressão diminui bruscamente, o líquido pode vaporizar, gerando bolhas de vapor. Essas bolhas estouram e geram jatos de líquido muito rápidos, que se chocam com as pás do impelidor. Esses choques causam o desgaste o equipamento, além de ruídos e vibração.
Dá uma olhadinha no que acontece:
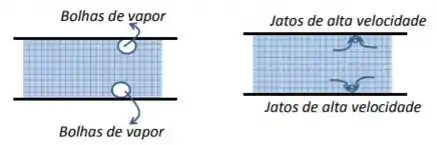
Para um líquido se vaporizar, a gente já sabe que a pressão () no olho do impelidor tem que ser menor que a pressão de saturação do líquido (). Então, para evitar a cavitação, temos que garantir que:
Bora dar uma olhadinha numa bomba em um sistema qualquer aqui em baixo:
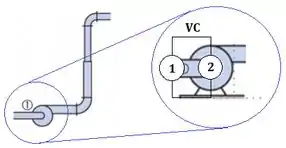
Podemos aplicar a equação da energia nesse volume de controle () que envolve a bomba:
Note que tem um termo a mais para a região do ponto , porque é onde o fluido é rotacionado. Assim, nós adicionamos o termo de energia cinética e rotação, em que: é a velocidade relativa entre o fluido e o rotor e é um parâmetro da própria bomba.
Quando uma bomba está quase na iminência de cavitação, a gente sabe que:
Então, a equação fica:
Como as alturas nos pontos e são as mesmas () e o trabalho sobre a bomba é nulo (), temos que:
Rearranjando a equação, teremos:
Dessa equação definimos um conceito muito importante: o (Net Positive Section Head).
NPSHD e NPSHR
Mas que negócio é esse todo em inglês? Calma, pequeno gafanhoto! Vamos entender juntinhos o que é essa parada. O nada mais é do que a energia medida em termos da pressão do sistema (altura de carga), medido em metros.
Da equação que encontramos, temos que:
- Lado esquerdo: refere-se ao disponível (), que varia conforme o fluido e o sistema em questão
- Lado direito: refere-se ao requerido (), que depende da bomba e é especificado pelo fabricante.
“Mas o que isso tem a ver com cavitação?” Tem tudo a ver! Bora entender o porquê?
Se o NPSH é a carga e temos uma parcela que é disponível pelo sistema e outra que é requerida pela bomba, precisamos que a pressão disponível seja maior do que a pressão requerida pela bomba, para que não haja cavitação.
Ou seja, em termos práticos, para evitar a cavitação o NPSH Disponível deve ser maior que o NPSH requerido.
Logo, a cavitação começa a acontecer quando . Essa condição será muito pedida nos exercícios! Quando o NPSHR é maior que o NPSHD, aí o sistema já está cavitando mesmo e isso não é o que queremos! Combinado? o/
Só para reforçar, sistema funcionando direitinho significa que . Vamos guardar isso no coração
Os exercícios de cálculo de bomba retomam o assunto de perda de carga que já vimos! Então, se achar necessário, dá uma olhadinha de novo nesse material ^^
NPSHD e NPSHR
Exercícios Resolvidos
Exercício Resolvido #1
Concurso 2011 da Petrobras – Químico de Petróleo Júnior
(Adaptada) Com relação ao fenômeno de cavitação, analise as afirmativas abaixo:
- Os principais inconvenientes da cavitação são barulho, vibração, alteração das curvas características e danificação dos materiais.
- Para que não ocorra cavitação em bombas, é necessário que o requerido seja maior que o disponível.
- Uma forma de evitar a cavitação é reduzir as perdas de carga na sucção e aumentar o diâmetro dos tubos e conexões.
Qual(is) das afirmações é(são) verdadeira(s)?
Passo 1
Bora avaliar cada opção, para gente decidir juntos qual a reposta correta!
- Os principais inconvenientes da cavitação são barulho, vibração, alteração das curvas características e danificação dos materiais.
- Para que não ocorra cavitação em bombas, é necessário que o requerido seja maior que o disponível.
- Uma forma de evitar a cavitação é reduzir as perdas de carga na sucção e aumentar o diâmetro dos tubos e conexões.
Essa afirmação é verdadeira! A cavitação ocorre em bombas devido à vaporização do líquido, que gera, por sua vez, bolhas. Tais bolhas, ao se colapsarem, acabam provocando em choques mecânicos com a carcaça do equipamento. Os choques ocasionam em barulho, vibração e desgaste do material e isso diminui o desempenho da máquina.
Essa afirmação é falsa. Para evitar a cavitação temos que garantir que a carga (pressão) disponibilizada pelo sistema () seja superior à carga requerida () pela bomba. Dessa forma, não observamos a formação de bolhas!
Essa afirmação é falsa. Se reduzirmos as perdas de carga na sucção (entrada na bomba), estaremos entrando com um fluido de maior pressão e isso realmente evita a cavitação. Pela equação de , podemos ver também:
Quanto menor a perda de carga, menor será o e, consequentemente mais longe a bomba estará da cavitação.
Ao aumentar o diâmetro das tubulações, provocará a diminuição da vazão e, consequentemente, da velocidade do escoamento. Como sabemos: quanto menor a velocidade, maior a pressão.
Ao aumentar o diâmetro das conexões, estaremos aumentando a perda de carga desses acidentes e, pela equação de , vemos que ele aumentará! Logo, isso aumenta a tendência de cavitação.
Resposta
A única alternativa correta é a opção I.
Exercício Resolvido #2
Concurso 2010 da Petrobras Biocombustível – Engenheiro de Processos Júnior
(Adaptada) Usa-se uma bomba centrífuga para transferir um solvente volátil de um tanque para outro. O solvente pode ser considerado como um fluido newtoniano e incompressível, com escoamento em regime plenamente turbulento. O relatório técnico das últimas mostra que, às , a referida bomba operava com carga positiva de sucção disponível () igual à requerida () e que, no referido período, a temperatura ambiente variou conforme mostrado na tabela abaixo:

Sabendo-se que os tanques, a tubulação e a bomba estão permanentemente expostos ao meio ambiente e que as demais variáveis envolvidas permaneceram inalteradas no referido período, estime por quanto tempo a bomba operou sob cavitação.
Passo 1
E aí, galerinha! Bora resolver esse pepino!
Como a gente já viu, para evitar a cavitação, temos que garantir que:
Como o depende somente das especificações da bomba, ele será constante. Bora avaliar o então:
Beleza! Mas o problema não fala de mudanças na pressão e nem na velocidade! Ele fala de temperatura e, se você olhar a equação, a temperatura não entra na equação do . “E agora?”
Calma, pequeno padawan! ahah Dá uma olhadinha de novo para a equação! A temperatura não está explícita, mas ela interfere na pressão de saturação () dos líquidos! TCHARAM!
Se você aumenta a temperatura de um sistema contendo uma substância volátil, aumenta a tendência dela vaporizar e, consequentemente, sua pressão de vapor aumenta!
Passo 2
Agora a gente sabe que tem que olhar para a pressão de saturação. Então, dá uma olhada de novo na equação do :
Veja que quanto maior for a pressão de vapor (), menor será o .
Pelo enunciado, às , a bomba operava com:
Ou seja, a bomba está na iminência da cavitação! Nesse horário, a temperatura ambiente era de . Então, em temperaturas maiores que , a pressão de saturação do solvente será maior e, consequentemente, o será menor.
Portanto, em temperaturas acima de , ocorrerá a cavitação. Observando a tabela, vemos que isso corresponde ao período de às .
Resposta
A bomba cavitou no período de às .
Exercício Resolvido #3
Concurso 2010 da Petrobras Biocombustível – Engenheiro de Processos Júnior
(Adaptada) Em determinada indústria, a bomba centrífuga será substituída pela que, sabe-se de antemão, vai operar com uma vazão maior que a de . Designando a carga positiva de sucção disponível das bombas e por, respectivamente, e , considerando que o regime de escoamento com a bomba era plenamente turbulento e mantidas inalteradas as demais variáveis envolvidas, determine qual das cargas é maior ( ou ).
Dado: A Carga Positiva de Sucção () corresponde ao termo da língua inglesa Net Positive Suction Head ().
Passo 1
Sabemos que o é definido como:
Ao modificarmos a vazão, estaremos alterando a velocidade do fluido nos tubos e, consequentemente, a perda de carga () também mudará.
A gente já viu que a perda de carga em tubos é dada pela seguinte expressão:
Vamos colocar a velocidade em função da vazão volumétrica () pra ficar mais fácil de visualizar:
Assim:
Concluimos, então, que, ao aumentar a vazão volumétrica (), a perda de carga () também aumenta! Dessa forma, esperamos que a perda de carga seja maior no sistema do que no sistema , porque, pelo enunciado, a vazão é maior que a vazão :
Então:
Logo:
Considerando que só o tubo contribui para a perda de carga, temos:
Você pode se perguntar: “Mas o fator de atrito () também não varia com a vazão, já que ele é função do número de Reynolds?”
Nessa situação aqui ele não vai variar! Lembre-se de que o fator de atrito para escoamentos plenamente turbulentos não depende do número de Reynolds, ele só varia com a rugosidade ().
Como os tubos serão os mesmos, a rugosidade será igual em ambos os sistemas e, consequentemente, os fatores de atrito também serão iguais!
Passo 2
Agora, bora analisar a equação do :
Como a diferença de pressão e a altura relativa entre os reservatórios é igual em ambos os sistemas, temos que o diminui quando aumenta a perda de carga (). Logo:
Em termos de :
Pronto! Resolvido mais esse exercício! ^^
Resposta
Exercício Resolvido #4
Concurso 2011 da Petrobras – Engenheiro de Processos Júnior
(Adaptada) Caso uma bomba em operação sofra cavitação, cite medidas que devam ser adotadas para corrigir esse problema em termos de:
- Nível de líquido no reservatório que alimenta a bomba.
- Diâmetro da tubulação.
- Velocidade de rotação da bomba.
Passo 1
A cavitação em bombas é o fenômeno em que o fluido se vaporiza, por conta de uma diminuição na pressão do mesmo. Isso pode ocorrer, porque o fluido é acelerado quando chega na bomba. Como a gente sabe: se aumenta a velocidade, diminui a pressão. Então, pronto! Acontece a cavitação!
Beleza! Entendido o problema! Mas, se você estivesse com esse problema, como você solucionaria? Lembre-se de que para evitar a cavitação, devemos garantir que:
Bora discutir, então, cada em um dos itens solicitados pelo enunciado maneiras de se aumentar o ou diminuir o !
Passo 2
a) Nível de líquido no reservatório que alimenta a bomba.
O sistema pode ser encarado de maneira geral da seguinte forma:
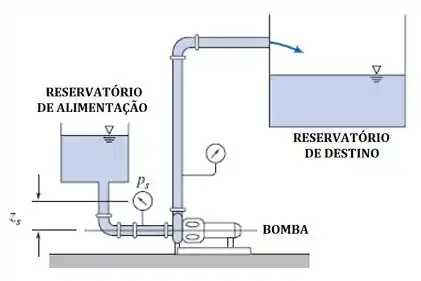
Então, como que a altura do tanque de alimentação poderia aumentar ?
Sabemos que o NPSHD é dado por:
Se aumentarmos a altura do tanque, aumentaremos a pressão do fluido na bomba (), pois maior será a energia potencial do fluido. Aumentando a pressão, estaremos consequentemente aumentando o como desejado!
Passo 3
b) Diâmetro da tubulação.
Bom, se considerarmos a vazão constante, podemos escrever que:
Beleza, assim, vemos que a velocidade é inversamente proporcional com o quadrado do diâmetro.
Portanto, se diminuirmos o diâmetro, teremos um aumento na velocidade. E se aumentarmos o diâmetro, teremos uma diminuição na velocidade
Agora, lembra aqui que o nosso NPSHD é dado por:
Ou seja, podemos considerer que o NPSHD é proporcional a velocidade…
Para que a nossa bomba não cavite, queremos aumentar o NPSHD e podemos fazer isso aumentando a velocidade.
E como a velocidade é inversamente proporcional ao diâmetro, para aumentar a velocidade diminuímos o diâmetro…
Passo 4
c) Velocidade de rotação da bomba.
A velocidade de rotação é um parâmetro que se refere a bomba em si, então ela modificará o . Como queremos que , devemos, então, diminuir o .
Sabemos que:
Logo, se diminuirmos a velocidade de rotação (), estaremos diminuindo como um todo o e, consequentemente, evitando a cavitação!
Resposta
a) Aumentar o nível de líquido no reservatório que alimenta a bomba.
b) Diminuir o diâmetro da tubulação.
c) Diminuir a velocidade de rotação da bomba.
Exercício Resolvido #5
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 815, ex. P 11.42
(Adaptada) Um modelo reduzido de bomba de 200 mm, fornecendo água a 82°C a 50,5 L/s e 2400 rpm começa a cavitar quando a pressão de entrada e a velocidade forem 82,7 kPa absoluta e 6,1 m/s, respectivamente. Encontre a NPSH requerida.
Passo 1
Esse enunciado nos conta uma história sobre uma boma que “começa a cavitar”, ou seja, ele está falando sobre uma iminência de cavitação
E na iminência de cavitação, o que acontece? Vimos na teoria que:
O enunciado pede simplesmente a NPSHR. Só que a fórmula para ela é essa aqui
E o enunciado não deu todas essas variáveis! Então é por isso que notar que estamos na iminência da cavitação é importante. Assim, vamos calcular a NPSHD que, pelos dados no enunciado, vai sair com mais facilidade =D
Passo 2
Bora lá! A NPSHD é essa camarada aqui
Vamos conferir se já conhecemos todas essas variáveis? Primeiro vamos lembrar de onde veio esse índice 1 aí na equação. Ele indica as variáveis de entradada na bomba
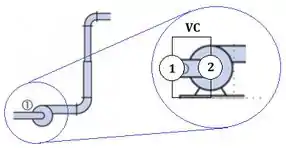
Então, é a pressão de entrada. O enunciado diz que Show!
é a velocidade média de entrada. Pelo enunciado:
Para descobrir a massa específica , vamos procurar por essa informação para a água a 82°C pois essa é a condição do escoamento!
Vamos descobrir a pressão de saturação de forma parecida: buscando em tabelas a para a água a essa temperatura
Agora sim, estamos prontos para aplicar na fórmula da NPSHD
Substituindo
Mas o exercício pediu NPSHR. Na iminência da cavitação:
Encontramos! Vamos para o próximo exercício! o/
Resposta
Exercício Resolvido #6
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 815, ex. P 11.42
(Adaptada) Um modelo reduzido de bomba de 300 mm, fornecendo água a 50°C a 60 L/s e 1200 rpm começa a cavitar quando a pressão de entrada e a velocidade forem 65 kPa absoluta e 3,4 m/s, respectivamente. Encontre a NPSH requerida por um protótipo que é 4 vezes maior
e gira a 600 rpm.
Passo 1
Opaaa! Essa questão é bem parecida com a anterior, mas acrescenta aqui a questão da semelhança entre bombas.
A situação é: temos uma bomba pequena e o enunciado dá informações suficientes para calcular seu NPSHR. Só que o enunciado pede o NPSHR de uma bomba semelhante a essa, porém de tamanho 4 vezes maior e sua rotação é metade da original.
É assim que se fazem os protótipos! O primeiro passo é calcular a NPSHR da bomba menor, que vamos chamar de modelo. A bomba maior é o protótipo.
Para calcular a NPSHR, vamos lembrar que estamos numa iminência de cavitação, ou seja:
Daí, vamos conseguir calcular o NPSHR com mais facilidade, pois sua fórmula tem variáveis que são mais fáceis de conhecer
Passo 2
Lembrando que
Do enunciado, sabemos que e
Além disso, como o fluido é a água a 50°C, consultando tabelas de referência, temos
Substituindo na equação do NPSHD
Como estamos na iminência da cavitação:
Passo 3
Agora, vamos analisar o protótipo pelas leis de semelhança
Onde p representa protótipo, m representa modelo, D é o diâmetro da bomba e n é o número de rotações do motor por unidade de tempo
Pelo enunciado
Substituindo
Simplificando
Então, na iminência da cavitação
A NPSH requerida do protótipo é 24,04 m
Resposta
Exercício Resolvido #7
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 816, ex. P 11.43
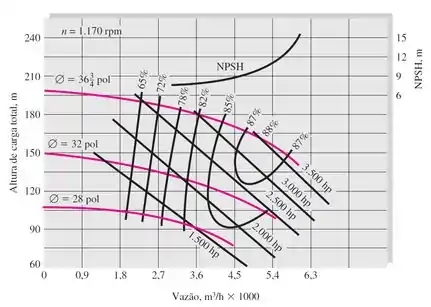
A bomba de 28 pol de diâmetro da figura a 1170 rpm é utilizada para bombear água a 20°C através de um sistema de tubulação a 833,3 L/s. (a) Determine a potência de eixo necessária. O fator de atrito médio é 0,018. (b) Se houver 19,8 m de tubo de 300 mm de diâmetro a montante da bomba, a que distância abaixo da superfície deverá ficar a entrada da bomba para evitar cavitação?
Passo 1
Esse exercício envolve o que falamos no tópico anterior (Curvas Características) e o atual (Cavitação). Pode cair assim na prova, então vamos juntos conectar esses conhecimentos 😊
A bomba de 28 polegadas é aquela da curva rosa mais embaixo da figura. A letra (a) do exercício pede a potência dessa bomba quando a vazão é 833,3 L/s.
A potência de eixo , como vimos na teoria de Curvas Características, pode ser calculada assim:
Além disso, a potência da bomba é essa aqui:
Então, a potência de eixo que queremos calcular é:
Do enunciado, sabemos que:
e estão no Sistema Internacional, falta converter a vazão volumétrica
Além disso, na figura, o eixo x é a vazão volumétrica em
Encontrando essa vazão na curva da bomba escolhida na figura, conseguimos encontrar a carga da bomba e a eficiência! Repara só:
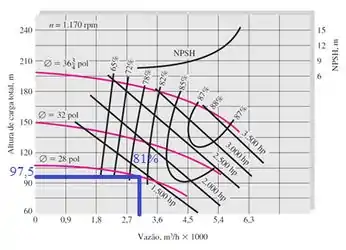
Pelo gráfico, encontramos os valores aproximados e . Encontramos 81% de eficiência, pois o ponto de operação se encontra entre as curvas de eficiência de 78% e 82%, estando mais próxima da segunda 😉 Mas é uma aproximação mesmo, você pode considerar outro valor próximo disso aí.
Substituindo os valores (no Sistema Internacional) na potência de eixo:
A potência de eixo é
Passo 2
Na letra b, o exercício pergunta qual seria a distância que a bomba deve ficar abaixo da superfície para não cavitar. Falou em cavitação, lembrou de NPSH. Mas como vamos calcular ele?
Pela fórmula:
Mas o enunciado não deu a velocidade média de entrada e nós não conhecemos .
“E agora, José?”
A resposta está na figura. Na vertical, do lado direito, olha só quem tá lá. Sim! A NPSH! =D UHUL! E na vazão ,
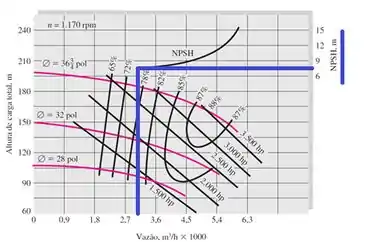
Passo 3
Agora que já sabemos o NPSH, vamos lembrar do objetivo do exercício: encontrar a distância abaixo da superfície que a bomba deve ficar para não cavitar.
O nosso volume de controle vai da superfície submetida a pressão atmosférica (1) até a entrada da bomba (2).
Como o início do percurso é a superfície, e essa é nossa referência, então e (na superfície, consideramos que a velocidade é nula pois a área é muito grande).
Além disso, não tem turbina e a bomba em si não está incluída do volume de controle (o VC vai até a entrada da bomba, onde não ocorreu a transferência de energia). Com isso nesse VC
Opa! Não conhecemos e (pressão e velocidade na entrada da bomba). Fica tranquilo, pois é aqui que o NPSH vai nos ajudar.
Na equação de energia, a gente vai adicionar e subtrair o mesmo termo, então não vamos modificar nada.
Mas assim o nosso NPSHD apareceu:
A partir de agora, vamos resolver essa equação aos poucos para encontrar o , que é a posição da entrada da bomba em relação à superfície.
Conhecemos ,
Além disso, pelas propriedades da água a 20°C, e
Substituindo na equação da energia
Simplificando
Vamos calcular a perda de carga agora. A perda que ocorre é a perda de carga global, calculada por essa equação:
Do enunciado, sabemos que . Para calcular V, vamos utilizar a vazão e a área do tubo nessa região (diâmetro = 300 mm = 0,3 m)
Substituindo
Finalmente na equação da energia
É isso aí! Por que esse sinal negativo? Pois a bomba deve ficar 5,8 m abaixo da superfície para evitar cavitação.
Resposta
a)
b) A bomba deve ficar 5,8 m abaixo da superfície para evitar cavitação.
Exercício Resolvido #8
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 816, ex. P 11.44
(Adaptada) Uma bomba de 18 pol de diâmetro de rotor opera em água no ponto de melhor rendimento a 1760 rpm. A NPSH obtida experimentalmente é de 4,9 m, e a perda por atrito entre a entrada e a bomba é 6,7m. Para evitar cavitação, será suficiente se a entrada da bomba for posicionada 2,7 m abaixo da superfície de um reservatório ao nível do mar?
Passo 1
Vamos começar anotando o que o enunciado disse
Então, vamos traçar nosso volume de controle entre a superfície do reservatório (1) e a entrada da bomba (2), pois conhecemos as variáveis nessas regiões.
Aplicando a equação da energia
Como o volume de controle não inclui a bomba em si e também não temos turbina
Lembrando que por definição, o NPSHD é
No nosso caso, a entrada da bomba é o ponto 2
Conseguimos substituir isso na equação da energia
Mas afinal, o que o exercício pede?

Queremos saber se as condições dadas de altura, perda de carga são suportadas pela bomba, ou seja, se a bomba consegue operar com essas condições. Em matematiquês
Passo 2
Vamos verificar se essa inequação é satisfeita então!
Substituindo os dados do enunciado
Além disso, (1) é uma superfície, então e
A da água a 20°C é 2300 Pa
Substituindo de novo
Calculamos o lado direito da desigualdade. O enunciado nos diz que o lado esquerdo (NPSH) é 4,9 m.
Para interpretar o resultado, vamos fixar o NPSH na equação da energia e calcular
Lembrando que
Ou seja, colocar a bomba 2,7 m abaixo da superfície dá uma margem de 1,2 m contra a cavitação.
Resposta
Sim, colocar a bomba 2,7 m abaixo da superfície é suficiente para evitar a cavitação.