Curva Característica de Bombas
Produzido por Raphael EloiTeoria
Fala, galera! Neste capítulo, a gente vai entender um pouco melhor o que são as curvas características das bombas, então bora lá!
Vamos ver um exemplo:
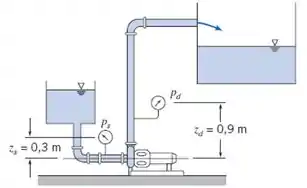
Beleza! Agora imagine que a gente vá fazer um experimento. Eu vou alterar a vazão que passa pela bomba e você vai ver pra mim quanto marca e , fechado?
Depois de vários pontos, a gente pode juntar tudo numa tabela como essa aqui em baixo:
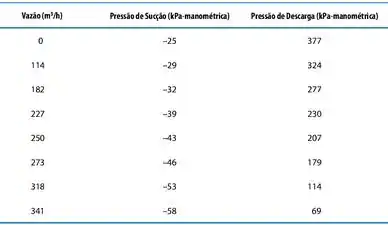
Antes de tudo, tem umas pressões negativas! Será que a gente errou em alguma coisa? :o
Não erramos não! Ahah Isso é porque estamos medindo a pressão manométrica, ou seja, ela é a diferença entre a pressão absoluta e a atmosférica, lembra? Então, se deu negativo, é porque a pressão no ponto é menor que a .
Agora, vamos ver o que tá acontecendo!
Como já esperávamos a pressão de descarga () é maior que a pressão de sucção (), afinal esse é o papel da bomba: aumentar a pressão do fluido.

Pra gente escolher a melhor bomba pro nosso sistema, precisamos saber qual a potência hidráulica () que cada uma fornece. A potência de uma bomba é a taxa de energia mecânica cedida ou retirada do fluido por uma máquina de fluxo.
Definimos a potência como sendo:
Em que é a vazão volumétrica, é a aceleração da gravidade e representa o aumento de carga proporcionado pelas bombas ou a diminuição de carga em turbinas.
Então, a gente precisa encontrar a carga que a bomba fornece () e, para isso, é só a gente aplicar a equação de Bernoulli entre a sucção e a descarga:
Admitindo que a velocidade do fluido não varia entre os dois pontos:
Vamos escolher um ponto para calcular a perda de carga: vamos pegar o ponto em que a vazão equivale a . Nesse ponto, a gente tem que
Então, a potência dessa bomba () na vazão de equivale a:
Calculando a eficiência:
Se soubermos ainda quanto de potência o motor da bomba () fornece, podemos calcular qual a eficiência da bomba (). Nessa vazão, sabemos que , então:
Beleza! Se fizermos esses cálculos para cada um dos pontos, a gente pode construir uma curva que mostra o comportamento da carga (), da potência () e da eficiência () com a vazão volumétrica (). Dá uma olhada em como ficaria:
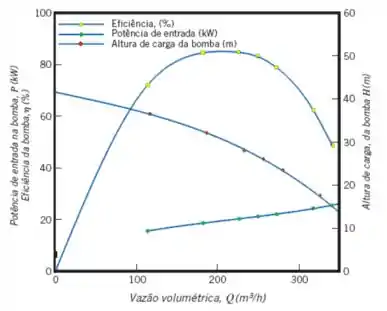
Definindo a curva característica:
A curva que mostra o comportamento da carga fornecida pela bomba () com a vazão é a denominada curva característica da bomba! Essa curva geralmente é dada pelo fabricante do equipamento da seguinte maneira:
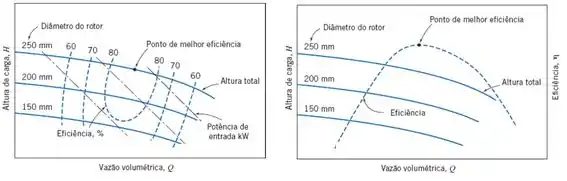
Nesse gráfico, a gente pode ver curvas para bombas com rotores de diferentes diâmetros, além das curvas de eficiência em tracejado (---).
Nossa função é escolher qual bomba fornece a carga necessária para atender o nosso sistema. Só que, para isso, a gente precisa calcular também a curva característica do sistema!
Pra construir a curva característica do sistema é bem parecido com o que fizemos para a bomba, basta a gente calcular qual a perda de carga total do sistema () para diferentes vazões volumétricas (). Assim, obtemos algo do tipo:
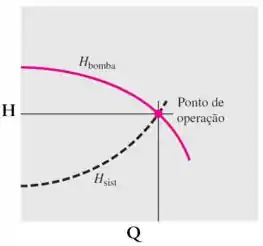
Tendo as duas curvas, a gente consegue comparar ambas e ver em qual ponto elas se cruzam, pois nesse ponto, teremos:
Esse é o ponto que denominamos ponto de operação. É nesse ponto em que toda a carga necessária pelo sistema é fornecida pela bomba ().
Em vazões menores, a bomba fornece uma carga maior que a necessária e, em vazões maiores, a bomba não é suficiente para atender a carga do sistema.
Bora ver como funciona isso na prática, então responde aí! ^^