Cálculo de Resistência com Integrais
Produzido por Bruno SoaresTeoria
Introdução
Lá atrás, vimos que para um resistor prismático (i.e. cubo, paralelepípedo, cilindro, etc) a resistência está associada à resistividade através da seguinte expressão:
Essa expressão só é válida se a resistividade for uniforme.
E o que acontece se a resistividade não for uniforme?! E se a área da seção transversal não for constante?!
Nesses casos, podemos calcular a resistência total partindo da resistência infinitesimal , dada por:
A coordenada deve ser adotada sempre na direção em que a corrente flui.
Por exemplo, se estivermos trabalhando com um resistor cilíndrico onde a corrente flui do raio interno , para o raio externo , então será a coordenada radial do sistema.
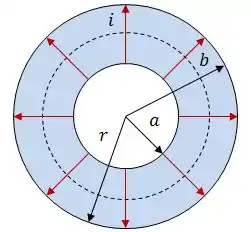
Agora, se no mesmo resistor cilíndrico a corrente flui entre as duas bases do cilindro, podemos usar a coordenada , ao invés de .
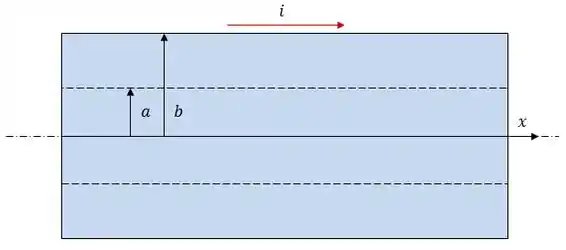
Esse é o espírito da coisa.
Esse tipo de questão aparece, geralmente, com resistores cilíndricos ou esféricos, e pode ser bem chatinha se você não for malandro (o que não é nosso caso), então vamos dar uma olhada em algumas possibilidades.
Área Transversal Variável e Resistividade Uniforme
Se a resistividade for uniforme, não precisamos nos preocupar com ela na hora da integração. Dessa forma, a resistência infinitesimal será dada por:
Conforme eu disse anteriormente, esse tipo de questão costuma aparecer com resistores cilíndricos e esféricos.
Assim, se o resistor for cilíndrico, a área será dada por:
Onde é o comprimento do resistor.
Caso o resistor seja esférico, a área será:
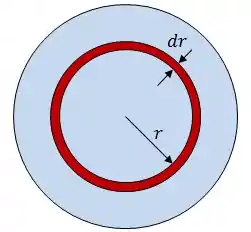
A ideia é basicamente essa.
Resistividade Não-Uniforme
Se a resistividade não for uniforme, o problema terá, necessariamente, que te informar uma função que representa a forma de como a resistividade varia de acordo com a coordenada radial (nos casos de resistores cilíndricos ou esféricos).
Assim, a resistência infinitesimal será dada por:
Com isso já podemos quebrar a cabeça nos exercícios.
Área Transversal Variável e Resistividade Uniforme
Resistividade Não-Uniforme
Exercícios Resolvidos
Exercício Resolvido #1
USP, P2 2010, Questão 2
Um resistor com resistividade , tem a forma de um cilindro oco de comprimento e raios e . Calcule a resistência e o módulo do vetor densidade de corrente no interior do resistor nos casos em que uma diferença de potencial é aplicada:
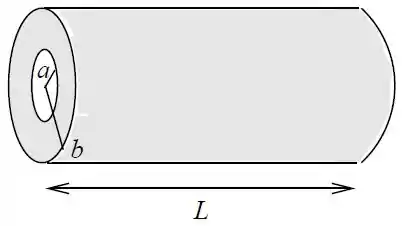
entre as bases do cilindro.
entre as superfícies interna de raio e a externa de raio .
Passo 1
entre as bases do cilindro.
Por definição, a resistência de um resistor é dada por:
Nesse caso, será a área da coroa circular de raios e .
Portanto:
Passo 2
Por definição, a densidade de corrente é dada por:
Usando a Lei de Ohm, podemos dizer que:
Lembrando que:
Logo:
Passo 3
entre as superfícies interna de raio e a externa de raio .
A ideia aqui é bem parecida com o que fizemos antes, a diferença é que, como a corrente agora flui radialmente, vamos ter que mudar a forma de calcular a resistência.
Vamos começar dividindo o cilindro em camadas cilíndricas de largura . Cada cilindro terá resistência , dada por:
agora será a área lateral do cilindro.
Logo:
Pra encontrar uma expressão pra , precisamos integrar esse cara, onde :
Passo 4
Pra calcular a densidade de corrente, vamos usar a mesma ideia que usamos anteriormente:
Lembrando que:
Logo:
Resposta
Exercício Resolvido #2
USP, P2 2015, Questão 1
Considere uma camada esférica condutora de raio interno e raio externo , conforme a figura.
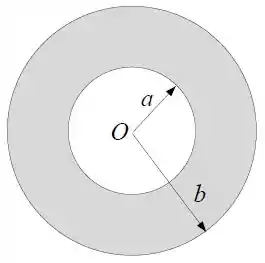
A resistividade da camada cresce linearmente com a distância ao centro , sendo dada por
Onde é uma constante positiva.
Determine a dimensão da constante no Sistema Internacional de Unidades.
Calcule a resistência elétrica da camada esférica na direção radial.
Uma diferença de potencial é aplicada entre as duas superfícies. Supondo que o potencial maior seja o da superfície interna, calcule a corrente e o vetor densidade de corrente.
Passo 1
Determine a dimensão da constante no Sistema Internacional de Unidades.
Vambora!
O aparece na fórmula da resistividade dada pelo problema, certo?
A única coisa que temos que fazer é analisar as dimensões que sabemos aqui.
Logo:
Logo, a dimensão de é Ohm.
Passo 2
Calcule a resistência elétrica da camada esférica na direção radial.
Como essa geometria é diferente da qual estamos acostumados, vamos começar pensando em uma camada infinitesimal, de resistência , espessura e área . Pela definição de resistência:
Agora ficou mais tranquilo... só temos que integrar esse cara nos limites .
O problema já nos disse que , logo, substituindo na expressão acima:
Passo 3
Uma diferença de potencial é aplicada entre as duas superfícies. Supondo que o potencial maior seja o da superfície interna, calcule a corrente e o vetor densidade de corrente.
Opa! Pra calcular a corrente ficou tranquilo, porque já temos a resistência e o problema falou da diferença de potencial .
Então é só usar a Lei de Ohm e ser feliz.
Passo 4
Se o potencial maior é o da superfície interna, isso quer dizer que a corrente flui da superfície interna para a superfície externa... isso que dizer que o vetor densidade de corrente vai estar na direção radial, de dentro para fora.
Por definição, a densidade de corrente é dada por:
Como aqui a área vai depender do raio , basta substituir isso na fórmula acima.
Logo:
Pra finalizar, basta substituir aqui a expressão que encontramos para a corrente ali em cima.
Simplificando:
Resposta
A dimensão de é Ohm .
Exercício Resolvido #3
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 2 , 8º ed. Rio de Janeiro: LTC , 2006, pp 162-35
Na figura abaixo uma corrente elétrica atravessa um tronco de cone circular reto de resistividade , raio menor , raio maior e comprimento . A densidade de corrente é uniforme ao longo de uma seção reta perpendicular ao eixo do objeto. Qual é a resistência do objeto?

Passo 1
Então, pessoal! Temos mais um condutor, dessa vez em forma de tronco de cone.
Os dados foram:
Só com isso a gente consegue calcular? Acho que sim, né? Vamos lá!
Passo 2
A gente sabe, pela Lei de Ohm, que .
Como a corrente ta fluindo entre as bases, deveremos usar:
Mas e essa área em função de aí como a gente calcula?
Cara, como o condutor diminui de raio linearmente fica até fácil de calcular, e com uma função bem tranquila, de 1° grau mesmo.
É só achar essas constantes. Como a gente faz isso? Substituindo valores que a gente já sabe, as extremidades.
Considerando a origem , ou seja, no ponto em que a seção tem raio , teremos:
Quando teremos:
Logo
Passo 3
Como , teremos que:
Agora usando a nossa integral linda lá, teremos:
Vixe! Que feio! Mas lembra que isso aí era algo do tipo
Substituindo os valores, encontraremos:
Resposta
Exercício Resolvido #4
USP, P2 2014, Questão 1
A região entre duas cascas esféricas condutoras concêntricas de raios e com é preenchida com um material de resistividade elétrica , onde é a distância até o centro das cascas esféricas e é uma constante.
Ligando-se uma bateria às cascas esféricas como na figura observa-se uma corrente no sentido indicado.
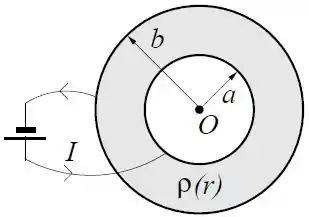
- Calcule o vetor densidade de corrente na região entre as cascas .
- Usando a lei de Ohm, determine o vetor campo elétrico entre as cascas esféricas.
- Calcule a resistência desse sistema em função de , e .
Passo 1
- Calcule o vetor densidade de corrente na região entre as cascas .
- Usando a lei de Ohm, determine o vetor campo elétrico entre as cascas esféricas.
- Calcule a resistência desse sistema em função de , e .
Sabendo que a corrente sai da placa maior da fonte (ali na esquerda da figura), corre o circuito e volta para a placa menor, a gente consegue ver que a corrente vai fluir da casca menor para a casca maior.
Beleza! Além disso, a densidade de corrente está relacionada com a corrente através da seguinte equação:
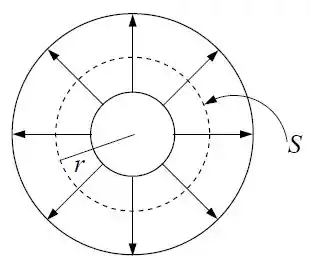
Agora é só resolver a integral e acabou!
Já sabemos que a resistividade depende de ... logo, a densidade de corrente também vai depender de .
A integral vai ser exatamente a área da superfície , de raio . Portanto:
Ah! Você só não pode esquecer de um detalhe muito importante... o problema pediu pra calcular o vetor densidade de corrente. Então faltou especificarmos a direção e o sentido da corrente.
A parada é que nós acabamos falando disso aqui em cima. Quando falamos que a corrente vai fluir da casca esférica menor para a casca esférica maior, no fundo nós falamos que a densidade de corrente tem a direção radial, apontando pra fora... do mesmo jeito que representamos na última figura.
Portanto:
Passo 2
Vamos lá! A lei de Ohm nos permite relacionar a densidade de corrente com o campo elétrico através da seguinte equação:
Onde é a resistividade. Agora ficou fácil para nós!
Só vamos ter o trabalho de substituir o que o problema nos disse e o que achamos no passo 1.
Passo 3
Beleza... o melhor caminho pra calcular essa resistência é através da relação:
Mas pra isso nós temos que encontrar a diferença de potencial . Pô! Mas na letra (b) nós calculamos o campo elétrico, certo?
Show! Podemos relacionar o campo elétrico com o potencial pela expressão:
Voltando pra nossa primeira relação:
Resposta
Exercício Resolvido #5
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Problema 25.64, pp. 164.
A região entre duas esferas concêntricas condutoras com raios e está preenchida por um material condutor com resistividade constante.
a) Mostre que a resistência entre as esferas é dada por
b) Deduza uma expressão para a densidade de corrente em função do raio em termos da diferença de potencial entre as esferas.
c) Mostre que o resultado da parte (a) se reduz a
quando a distância entre as esferas é pequena.
Passo 1
a) A situação que a gente tem nesse caso é dado na Figura abaixo. Se a corrente atravessa a região entre as esferas condutoras no sentido radial, então ela atravessa uma área de e um elemento de comprimento.
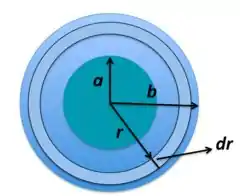
Por isso, ao atravessar esse comprimento com área , a resistência oferecida à corrente nesse trajeto é dada por
Agora, para sabermos a resistência total, temos que integrar de , raio da esfera interna, até , que é o raio da esfera externa e isso nos dá que
Simplificando um pouco mais a expressão anterior, temos
Passo 2
b) Sabemos que a densidade de corrente é dada por , sendo que ( ) é o raio de superfície esférica através da qual a corrente passa.
Mas, como e temos a resistência dada no item (a), a densidade de corrente pode ser reescrita como
expressão que simplificada resulta em
Passo 3
c) Fazendo a distância pequena, temos que a resistência total é dada por
em que é a área da esfera interna.
Resposta
Exercício Resolvido #6
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Problema 25.76, pp. 164.
Um cilindro de comprimento e raio é feito de uma mistura complexa de materiais. Sua resistividade depende da distância da extremidade esquerda e obedece à fórmula
em que e são constantes. Na extremidade esquerda, a resistividade é de , e a do lado direito é de .
- Qual é a resistência desse bastão?
- Qual é o campo elétrico na metade do seu comprimento, se ele carregar uma corrente de ?
- Se cortarmos o bastao em dois segmentos de , qual é a resistência de cada metade?
Passo 1
a) De acordo com a Figura abaixo, a resistência infinitesimal pode ser escrita como
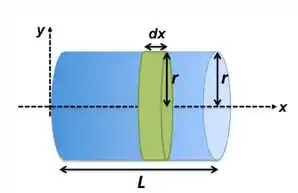
Onde a area é a área da seção reta do cilindro que é um círculo:
Agora, repara que a gente não conhece os valores das constantes e . Para encontrá-los, sabemos, pelo enunciado, que
e que
Resolvendo a última equação acima utilizando o valor de obtido com , temos
Portanto,
Essa é a nossa expressão para a resistividade!
Passo 2
Substituindo os valores das constantes na integral e integrando em todo o comprimento do cilindro teremos:
onde tiramos o da integral, pois esse valor é fixo ao longo de todo o cilindro. Ok? Fica atento, porque se fosse um tronco de cone, por exemplo, esse raio poderia variar ao longo do eixo . Mas aqui neste caso, é fixo, o que facilita nossa vida…
Continuando com a integral acima, quando a resolvemos, obtemos que a resistência total do cilindro é
Substituindo os valores do raio do cilindro e do comprimento , encontramos o valor da resistência .
Passo 3
b) A gente viu que a lei de Ohm mostra que , ou seja, ela mostra uma relação de proporcionalidade entre o campo elétrico e densidade de corrente . Mas o que precisamos encontrar neste item é o campo no ponto , que é dado por
Portanto, como foi um valor dado e conhecemos a área, só precisamos encontrar a resistividade nesse ponto:
E substituindo o valor do comprimento teremos:
E assim, encontramos o campo elétrico
E substituindo o raio do cilindro e a corrente , teremos:
Passo 4
c) Considerando que a primeira metade do cilindro tem resistência , teremos que mudar o limite superior de integração lá do Passo 1 para obter que
Substituindo os valores do enunciado, teremos que
Essa é a resistência da primeira metade do cilindro.
Agora, para obter qual é a resistência da segunda metade do cilindro que vai de a , a gente precisa subtrair da resistência total , ou seja,
Portanto, a segunda metade tem uma resistência maior que a primeira.
É claro que uma outra alternativa aqui é pegar a integral lá do Passo 1 e mudar o limite inferior de integração para e o limite superior para . Isso tem que dar o mesmo valor que a gente obteve acima e é uma boa forma de você também treinar o raciocínio.
Resposta
Exercício Resolvido #7
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Problema 25.85, Adaptada, pp. 167.
A resistividade de um semicondutor pode ser alterada adionando-se diferentes quantidades de impurezas. Uma barra de um semicondutor de comprimento e seção reta de área está ao longo do eixo , entre e . O material obedece à lei de Ohm e sua resistividade varia ao longo da barra, de acordo com a relação
A extremidade da barra para está a um potencial mais elevado do que o potencial da extremidade .
- Calcule a resistência total da barra e a corrente que flui através dela.
- Determine o módulo do campo elétrico na barra em função de .
- Calcule o potencial .
Passo 1
a) Como mostramos na Figura abaixo, o que temos é um material com área constante, com resistividade que varia exponencialmente ao longo do eixo .
Por isso, o elemento de resistência , quando integrado de a , resulta em
Aqui, a área foi retirada da integral porque é constante ao longo de todo o comprimento da barra. Fica atento a isso, porque podem aparecer exercícios na sua vida aí em que a área pode mudar!!!
Voltando lá na integral e resolvendo, a gente chega em
que , nesse caso, fornece o valor da resistência total da barra de comprimento .
Com isso, a corrente é obtida como
Agora, para um valor de arbitrário, temos que a resistência é dada por
Passo 2
b) Sabemos, pela lei de Ohm, que
que, se simplificamos, teremos que
Passo 3
c) Quando , o enunciado fala para a gente que o potencial é . Após a corrente atravessar um comprimento da barra, teremos uma queda de potencial igual a por causa do material da barra. Portanto, o potencial depois de a corrente percorrer uma distância da barra é dado por
Substituindo os valores de e que encontramos, teremos
Essa expressão simplificada fica assim