Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Resistividade

Ver Todos os Exercícios

Teoria

Fala aí! Seja muito bem vindo ao Responde Aí! Bora conversar sobre Resistividade e Resistência Elétrica?

O que é Resistividade Elétrica?

A Resistividade Elétrica é uma característica de cada material e nos diz o quanto esse material se opõe à passagem de corrente elétrica. Ela é a razão entre o módulo do campo elétrico num elemento de circuito e o módulo da densidade de corrente:

A unidade de medida da resistividade é “Ohm metro” . Quanto maior a resistividade, menor a tendência do elemento de circuito de deixar passar os elétrons.

Fórmula da Resistividade Elétrica

Na prática a fórmula que mais vamos usar é a Segunda Lei de Ohm que relaciona a Resistência Elétrica, a Resistividade e as dimensões do material da seguinte forma:

Onde:

  •  é a resistência do fio, medida em Ohms
  •  é uma constante chamada de resistividade, que varia de acordo com o material do fio, medida em
  •  é o comprimento do fio, medido em metros
  •  é a área da seção transversal do fio, medida em metros quadrados

Tabela de Resistividade Elétrica

Na tabela a seguir podemos conferir a resistividade de alguns materiais:

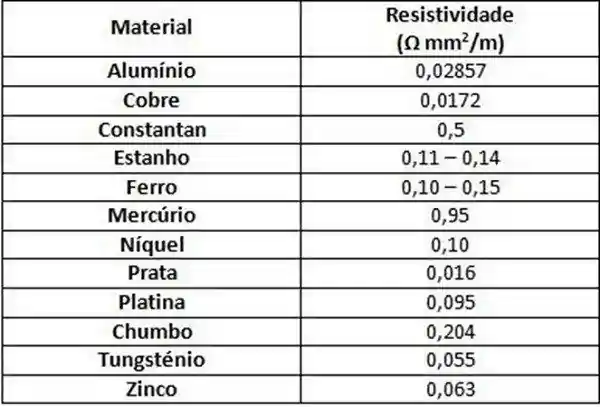
Tabela de Resistividade Elétrica
Tabela de Resistividade Elétrica

Na tabela acima podemos conferir a resistividade de alguns materiais condutores. Um material condutor é um material com baixa resistividade e por isso as cargas elétricas se movem com facilidade por ele, um exemplo de material condutor do nosso dia a dia é o cobre! Ele tem baixíssima resistividade e por isso é muito utilizado em fiações elétricas.

Com um material isolante temos a situação contrária, sua resistência é alta e as cargas elétricas quase não conseguem se mover. Um exemplo de material isolante é a borracha, é por isso que quando você vai mexer com alguma fiação na sua casa e coloca o chinelinho pra não levar choque!

O Responde Aí preparou um resumindo em vídeo super completo, sobre resistência e resistividade! Dá só uma conferida 👇

📢Clique para saber mais:

Qual é a Diferença entre Resistência e Resistividade?

A Resistência é uma medida do quanto um certo material resiste à passagem de cargas nele. Já Resistividade é uma característica do material e funciona como uma constante!

Resistência Elétrica e a Primeira Lei de Ohm

A Resistência é medida em (Ohm) e pode ser calculada em função da corrente resultante e da diferença de potencial em um material condutor .

Essa relação é dada pela Primeira Lei de Ohm:

Onde a diferença de potencial é dada por Volts e a corrente por Ampère .

Condutividade

A condutividade é o inverso da resistividade, ou seja, esta relacionada com a habilidade de um material conduzir corrente elétrica, ela é definida por:

Dessa forma:

Essa é uma outra forma de escrever a Segunda Lei de Ohn!

Agora vamos praticar com exercícios?

Qual é a Diferença entre Resistência e Resistividade?

Condutividade

Exercícios Resolvidos

Exercício Resolvido #1

UERJ- Lista de Exercícios sobre Correntes Elétricas.

A figura é o gráfico corrente versus diferença de potencial para um material. Qual é a resistência do material?

Passo 1

Para qualquer material condutor, temos que a cada ponto V = R . I , para um condutor ôhmico, temos que a resistência é constante, e no caso de um gráfico V por I é inclinação da reta. No gráfico mostrado, que é I por V , temos que a resistência será:

R = Δ V Δ I

R = 100 2 = 50 1 = 50   Ω

Resposta

R = 50   Ω

Exercício Resolvido #2

UFRJ, PF 2014.2, ME 8

Uma barra de cobre cilíndrica, de resistência elétrica R , comprimento L e seção reta A , é comprimida para a metade do seu comprimento original, sem que seu volume se altere.

Pode-se afirmar que o novo valor de sua resistência elétrica é:

a 4 R

b 2 R

c R / 2

d R / 4

e R

Passo 1

A resistência R , por definição é dada por:

R = ρ L A

Precisamos primeiro encontrar as relações para L ' e A ' . Mas como, ao ser comprimida, o seu volume não se altera, podemos dizer que:

V = L A = L ' A '

Onde L ' = L / 2 , logo:

L A = L A ' 2 → A ' = 2 A

Portanto, a nova resistência será dada por:

R ' = ρ L ' A ' = ρ L 2 2 A

R ' = ρ L 4 A → R ' = R 4

A opção certa é a letra d .

Resposta

d R / 4

Exercício Resolvido #3

UERJ- Lista de Exercícios sobre Corrente Elétrica.

Quando 115   volts são aplicados entre as extremidades de um fio que possui 10   m de comprimento e 0,30   mm de raio, a densidade de corrente é igual a 1,4 × 10 4   A/ m 2 .

Determine a resistividade do fio.

Passo 1

Bom, o problema nos dá a voltagem V , o comprimento do fio L e o raio r do mesmo, além da densidade de corrente J .

Como ele está pedindo a resistividade ρ do fio, temos que dar um jeito de ligar todas essas coisas.

A resistividade ρ do fio é relacionada com a resistência R através dessa fórmula:

R = ρ L A

ρ = R A L

Como o problema nos deu L e nós conseguimos encontrar a área através do raio r que o problema nos deu, temos que dar um jeito de encontrar o valor de R .

Passo 2

Temos que:

V = R I

Show de bola! Nós temos V e não temos I ... mas o problema falou em densidade de corrente J , então nós só temos que lembrar que:

J = I A

I = J A

Substituindo na equação que define a resistência, teremos:

V = R J A

R = V J A

Antes de sair tacando os valores aqui, vamos jogar na fórmula da resistividade que encontramos ali em cima. ;)

Passo 3

ρ = R A L

Substituindo a fórmula da resistência R que encontramos no Passo 2:

ρ = V J A ⋅ A L

Simplificando isso aqui, teremos:

ρ = V J L

Onde:

V = 115   V ;

J = 1,4 × 10 4   A/ m 2 ;

L = 10   m ;

Logo:

ρ = 115 1,4 × 10 4 × 10

ρ = 8,21.10 - 4   Ωm

Aqui vai uma dica importante, tá vendo que, organizando tudo pra só depois substituir os valores nós acabamos simplificando um pouco a nossa vida, não tendo que calcular a área da seção transversal do fio?

Eu sempre achei uma boa, principalmente em física, fazer isso pra resolver os problemas... então fica a dica.

Resposta

ρ = 8,21.10 - 4   Ωm

Exercício Resolvido #4

Halliday/ Resnick, Fundamentos da Física Volume 3, 8ª ed. LTC, Cap. 26, pp. 160-15

Um fio de Nichrome (uma liga de níquel, cromo e ferro muito usada em elementos de aquecimento) tem 1,0   m de comprimento e 1,0   m m 2 de seção reta e conduz uma corrente de 4,0   A quando uma diferença de potencial de 2,0   V é aplicada a suas extremidades.

Calcule a condutividade σ do Nichrome.

Passo 1

Ok, pra calcular a condutividade, precisamos começar calculando a resistividade.

Pra começar, vamos usar a corrente e a diferença de potencial que o problema forneceu pra calcularmos a resistência e, a partir disso, calculamos a resistividade, beleza?

A resistência é dada por:

R = V i

Onde:

V = 2,0   V

i = 4,0   A

Logo:

R = 2 4

R = 0,5   Ω

Passo 2

A resistência está associada com resistividade através da equação:

R = ρ L A

Assim, a resistividade será:

ρ = R . A L

Onde:

A = 1,0   m m 2 = 10 - 6   m 2

L = 1,0   m

Logo:

ρ = 0,5 × 10 - 6 1

ρ = 5,0 × 10 - 7   Ω . m

Passo 3

Finalmente, a condutividade será:

σ = 1 ρ

σ = 1 5,0 × 10 - 7

σ = 2,0 × 10 6   Ω . m - 1

Resposta

σ = 2,0 × 10 6   Ω . m - 1

Exercício Resolvido #5

UFRJ, PF 2015.1, ME 6

Três resistores cilíndricos circulares ôhmicos, 1, 2 e 3, são construídos com o mesmo material, de resistividade conhecida ρ . O resistor 1 tem comprimento L e área de seção reta A , o resistor 2 tem comprimento L e área de seção reta 2 A , enquanto o resistor 3 tem comprimento 2 L e área de seção reta 2 A .

Se cada um desses resistores for submetido a uma mesma diferença de potencial entre suas extremidades, podemos afirmar, sobre os módulos J i   i = 1 ,   2 ,   3 das densidades de corrente que fluem ao longo deles, que

a J 1 = J 2 = J 3 .

b J 1 = J 2 / 2 = J 3 .

c J 1 = J 2 = J 3 / 2 .

d J 1 = 2 J 2 = J 3 .

e J 1 = J 2 = 2 J 3 .

Passo 1

A densidade de corrente, por definição, é dada por:

J = I A

A corrente no resistor está associada com a resistência por I = V / R , logo:

J = V R A

Por definição, a resistência é dada por:

R = ρ L A

Substituindo isso na expressão de J , teremos:

J = V ρ L A A

Finalmente:

J = V ρ L

Agora podemos cair dentro do problema.

Passo 2

Vamos escrever as densidades de corrente de cada material, ok?

  • Resistor 1:

    • O resistor 1 possui comprimento L e área transversal A , logo:

    J 1 = V ρ L

  • Resistor 2:

    • O resistor 2 tem comprimento L e área de seção reta 2 A , logo:

    J 2 = V ρ L

  • Resistor 3:

O resistor 3 tem comprimento 2 L e área de seção reta 2 A , logo:

J 3 = V 2 ρ L

Assim, as três densidades de corrente estão associadas por:

J 1 = J 2 = 2 J 3

A resposta certa é a letra e .

Resposta

e J 1 = J 2 = 2 J 3 .

Exercício Resolvido #6

Halliday/ Resnick, Fundamentos da Física Volume 3, 8ª ed. LTC, Cap. 26, pp. 165-72

Os enrolamentos de cobre de um motor têm uma resistência de 50   Ω a 20 ° C quando o motor está frio. Depois de o motor trabalhar durante várias horas, a resistência aumenta para 58   Ω .

Qual é a nova temperatura dos enrolamentos? Suponha que as dimensões dos enrolamentos não variem.

Dado: α = 4,3 × 10 - 3   K - 1 .

Passo 1

Como as dimensões dos enrolamentos não variam, a resistência varia com a temperatura da seguinte forma:

R - R 0 = R 0 α T - T 0

Assim, a nova temperatura dos enrolamentos será:

T = T 0 + R - R 0 R 0 α

Onde:

T 0 = 20 ° C

R 0 = 50   Ω

R = 58   Ω

α = 4,3 × 10 - 3   K - 1

Logo:

T = 20 + 58 - 50 50 × 4,3 × 10 - 3

T = 57,2 ° C

Resposta

T = 57,2 ° C

Exercício Resolvido #7

Halliday/ Resnick, Fundamentos da Física Volume 3, 8ª ed. LTC, Cap. 26, pp. 161-25

As especificações de uma lâmpada de lanterna são 0,30 A e 2,9 V (os valores da corrente e tensão de trabalho, respectivamente).

Se a resistência do filamento de tungstênio da lâmpada à temperatura ambiente 20 ° C é 1,1   Ω , qual é a temperatura do filamento quando a lâmpada está acesa?

Dado: α = 4,5 × 10 - 3   K - 1 .

Passo 1

A resistência do filamento quando a lâmpada está acesa é dada por:

R = V i

Onde:

V = 2,9 V

i = 0,3 A

Logo:

R = 2,9 0,3

R = 9,67   Ω

Passo 2

A resistência varia com a temperatura da seguinte forma:

R = R 0 ( 1 + α T - T 0 )

No enunciado ele falou que a resistência à temperatura ambiente é é 1,1 Ω . E a temperatura ambiente fica: 20 ℃ = 293 K .

Substituindo:

R = R 0 ( 1 + α T - T 0 )

9,67 = 1,1 ( 1 + 4,5 ⋅ 10 - 3 T - 293 )

Logo:

T = 8,79 - 1 4,5 ⋅ 10 - 3 + 293

T ≅ 2024   K

Logo,

T ≅ 1751 ℃

Resposta

T ≅ 175 1 ° C

Exercícios de Livros Relacionados

Uma barra de alumínio de seção reta quadrada tem 1,3 m de comprimento e 5,2 m m de lado. (a) Qual é a resistência entre as extremidades da barra? (b) Qual deve ser o diâmetro de uma barra cilíndrica d
Os enrolamentos de cobre de um motor têm uma resistência de 50 Ω a 20 º C º quando o motor está frio . Depois de o motor trabalhar durante várias horas, a resistência aumenta para 58 Ω . Qual é a nova
Quando um fio de metal é aquecido, não é apenas a resistividade que muda; o comprimento e a área do fio também são afetados. De acordo com a equação R=ρ L / A , as três grandezas devem ser levadas em
Se o número que indica o calibre de um fio aumenta de 6, o diâmetro é dividido por 2; se o calibre aumenta de 1, o diâmetro é dividido por 2 1 / 6 (veja a tabela do Problema 4). Com base nessas inform
Na Fig. 26-29, uma corrente elétrica atravessa um tronco de cone circular reto de resistividade 731 Ω · m , raio menor a = 2,00 m m , raio maior b = 2,30 m m e comprimento L = 1,94 c m . A densidade d