Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Densidade de Corrente Variável

Ver Todos os Exercícios

Teoria

Densidade de Corrente Não-Uniforme

Até agora a gente só viu fios nos quais a corrente é distribuída toda igualmente pela área do fio certo? E se eu te dissesse que é possível a corrente se concentrar mais em uma parte da área do fio do que em outra, como calcular a corrente que passa pelo fio se ela não tem um padrão?

Se liga nessas duas distribuições da corrente passando pela área da seção transversal do fio:

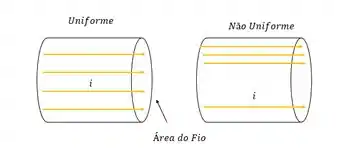
O fio onde a corrente é uniforme possui densidade de corrente constante e por isso o cálculo da corrente fica desse jeito aqui:

I = J . A

Pensa comigo... e se a corrente elétrica não estiver uniformemente distribuída na seção reta do condutor? O que eu faço?

Nesse caso, podemos calcular a corrente da seguinte forma:

d I = J → . d A →

Onde d I   é o escalar infinitesimal da corrente, J → é o vetor densidade de corrente e d A → é o vetor infinitesimal área que é perpendicular à área da seção transversal do fio.

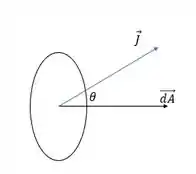
E se quisermos calcular a corrente que passa numa determinada área faremos o seguinte:

d I = J → ∙ d A →

Onde temos um produto escalar entre os vetores J → e d A → e por isso podemos fazer o seguinte:

d I = J d A c o s θ

E enfim integrando temos a corrente:

I = ∬ A   J → ∙ d A →

Ou se preferir:

I = ∬ A   J d A c o s θ

Eu sei que você está pensando: “Sério mesmo que apareceu uma integral dupla aí?!”.

Calma... na prática, nós temos como dar uma simplificada nisso, se liga.

Condutor de Seção Transversal Circular

Na maioria das vezes o fio tem forma circular, e quais considerações poderemos fazer nesses casos? Vamos ver calculando a corrente pro seguinte fio sabendo que a densidade de corrente é J → = 3 × 10 5 r A m 2 s ^ .  

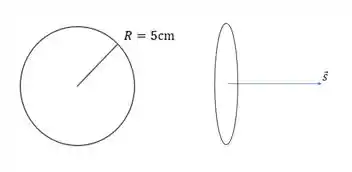
A gente sabe que pra encontrar a corrente precisamos fazer a seguinte integral.

I = ∬ A   J → ∙ d A → = ∬ A   J . d A c o s ( θ )

A primeira coisa importante é que o vetor J → será paralelo ao vetor d A → e teremos uma facilitação nas nossas contas pois nesse caso θ = 0 .

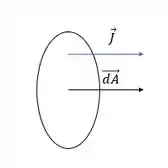
Na maioria dos casos o vetor densidade de corrente tá na direção do vetor d A → .

Olhando a figura a gente pode ver que ambos os vetores são normais ao plano, portanto paralelos entre si.

Daí a integral fica:

I = ∬ A   J . d A c o s 0 = ∬ A   J d A

Dali só falta a gente encontrar o infinitesimal da área, pra isso vamos pegar a equação da área do círculo:

A = π r 2

Derivando dos dois lados temos:

d A = 2 π r d r

O infinitesimal d r que aparece é a variação do raio ao longo da circunferência, se liga:

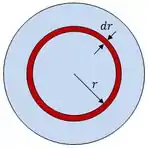
Fazendo essa substituição nós podemos transformar a integral dupla em simples pois não teremos que integrar em relação ao ângulo.

I = ∫ 0 R J 2 π r d r = 2 π ∫ 0 R J r d r

Se liga aí que o J tá dentro da integral, por quê? Porque estamos trabalhando com uma densidade de corrente variável, que varia ao longo da área conforme o raio.

Vamos substituir os valores e fazer a integral, se liga:

J = 3 × 10 5 r A m 2 ;     R = 0,05 m  

I = 2 π ∫ 0 0,05 3 × 10 5 r r d r = 2 π ∫ 0 0,05 3 × 10 5 r ² d r

Integrando e substituindo os limites temos:

I = 2 π r 3 3 × 3 × 10 5 0 0,05 = 2 π 0,05 3 × 10 5

E enfim a corrente no fio é:

I = 78,54 A

No geral os problemas vão trabalhar com seções circulares e daí é basicamente ir fazendo as substituições necessárias. Lembrando que a densidade de corrente variável será uma função do raio que precisa ser integrada, beleza? Bora pros exercícios?

Condutor de Seção Transversal Circular

Exercícios Resolvidos

Exercício Resolvido #1

Halliday/ Resnick, Fundamentos da Física Volume 3, 8ª ed. LTC, Cap. 26, pp. 160-11

O módulo J r da densidade de corrente em um certo fio cilíndrico é dado por J r = B r , onde r é a distância radial a partir do centro do fio em metros e B = 2,00 × 10 5   A / m 3 .

Qual é a corrente que passa em um anel concêntrico com o fio, com 10,0   μ m de largura, situado a uma distância radial de 1,20   m m do centro do fio?

Passo 1

Nesse caso, a densidade de corrente é dada por:

J r = d i d A

Como estamos trabalhando com um fio de seção reta circular, teremos:

d A = 2 π r   d r

Logo:

J r = d i 2 π r   d r

d i = J r . 2 π r   d r

Assim, podemos calcular a corrente através da integral:

i = ∫ a b 2 π r J r   d r

Onde a é o raio interno do anel, que vale a = 1,2 × 10 - 3   m . E b é o raio externo do anel, que vale b = 1,21 × 10 - 3 m .

Passo 2

Substituindo a função dada pelo problema, teremos:

i = ∫ a b 2 π r . B r   d r

i = 2 π B ∫ a b r 2   d r

i = 2 π B r 3 3 a b

i = 2 π B 3 b 3 - a 3

Substituindo os valores, teremos:

i = 2 π × 2 × 10 5 3 1,21 × 10 - 3 3 - 1,2 × 10 - 3 3

i = 1,82 × 10 - 5   A

i = 18,2   μ A

Resposta

i = 18,2   μ A

Exercício Resolvido #2

Halliday/ Resnick, Fundamentos da Física Volume 3, 8ª ed. LTC, Cap. 26, pp. 160-12

O módulo J da densidade de corrente em um certo fio cilíndrico de raio R = 2,00   m m é dado por J = 3,00 × 10 8 r 2 , com J em ampères por metro quadrado e a distância radial r em metros.

Qual é a corrente que passa em um anel concêntrico com o fio de raio interno 0,900   R e raio externo R ?

Passo 1

Nesse caso, a densidade de corrente é dada por:

J r = d i d A

Como estamos trabalhando com um fio de seção reta circular, teremos:

d A = 2 π r   d r

Logo:

J r = d i 2 π r   d r

d i = J r . 2 π r   d r

Assim, podemos calcular a corrente através da integral:

i = ∫ 0,9 R R 2 π r J r   d r

Passo 2

Substituindo a função dada pelo problema, teremos:

i = ∫ 0,9 R R 2 π r 3 × 10 8 r 2   d r

i = 2 π 3 × 10 8 ∫ 0,9 R R r 3   d r

i = 2 π 3 × 10 8 r 4 4 0,9 R R

i = π 3 × 10 8 2 R 4 - 0,9 R 4

i = π 3 × 10 8 2 R 4 - 0,6561 R 4

i = π 3 × 10 8 × 0,17195 R 4

i = 0,51585 × 10 8 π R 4

i = 5 , 1585 × 10 7 π R 4

Onde R = 2,00   m m = 2 × 10 - 3 m .

i = 5,1585 × 10 7 π × 2 × 10 - 3 4

i = 2,6 × 10 - 3   A

i = 2,6   m A

Resposta

i = 2 , 6   m A

Exercício Resolvido #3

Halliday/ Resnick, Fundamentos da Física Volume 3, 8ª ed. LTC, Cap. 26, pp. 160-13

Determine a corrente em um fio de raio R = 3,40   m m se o módulo da densidade de corrente é dado por a J a =   J 0 r / R e b   J b = J 0 1 - r / R , onde r é a distância radial e J 0 = 5,50 × 10 4   A / m 2 .

c Para qual das duas funções a densidade de corrente perto da superfície do fio é maior?

Passo 1

a J a =   J 0 r / R ;

A corrente é dada por:

i = ∫ 0 R 2 π r J a   d r

i = ∫ 0 R 2 π r J 0 r R   d r

i = 2 π J 0 R ∫ 0 R r 2   d r

i = 2 π J 0 R r 3 3 0 R

i = 2 π J 0 R R 3 3

i = 2 π R 2 J 0 3

Onde:

R = 3,40   m m = 3,4 × 10 - 3 m

J 0 = 5,50 × 10 4   A / m 2

Logo:

i = 2 π × 5,50 × 10 4 × 3,4 × 10 - 3 2 3

i = 1,33   A

Passo 2

b   J b = J 0 1 - r / R ;

i = ∫ 0 R 2 π r J b   d r

i = ∫ 0 R 2 π r J 0 1 - r R   d r

i = 2 π J 0 ∫ 0 R r - r 2 R   d r

i = 2 π J 0 r 2 2 - r 3 3 R 0 R

i = 2 π J 0 R 2 2 - R 3 3 R

i = 2 π J 0 R 2 2 - R 2 3

i = 2 π J 0 R 2 6

Onde:

R = 3,40   m m = 3,4 × 10 - 3 m

J 0 = 5,50 × 10 4   A / m 2

Logo:

i = 2 π × 5,50 × 10 4 × 3,4 × 10 - 3 2 6

i = 0,666   A

Passo 3

c Para qual das duas funções a densidade de corrente perto da superfície do fio é maior?

As duas funções são as seguintes:

J a = J 0 r R

J b = J 0 1 - r R

Para ver qual das duas funções é maior perto da superfície do fio, vamos fazer r = 0,99 R e ver o que acontece.

J a 0,99 R = 099 R . J 0 R → J a 0,99 R = 0,99 J 0

J b 0,99 R = J 0 1 - 0,99 R R → J b 0,99 R = 0,01 J 0

Logo, J a > J b .

Resposta

a

1,33   A

b

0,666   A

c

J a

Exercício Resolvido #4

Ufpe - Física 3 – PF 2018.1 - 2

A figura abaixo ilustra um cilindro condutor maciço de raio R que é percorrido por uma corrente elétrica I , onde 0 ≤ r ≤ R é a distância radial até o eixo de simetria do cilindro.

  1. Calcule a expressão para a corrente elétrica I quando a densidade de corrente J r = J 0 r / R , onde J 0 é uma constante.
  2. Calcule a expressão para a corrente elétrica I quando a densidade de corrente J = J 0 ( 1 - r / R ) , onde J 0 é uma constante.
  3. Dentre as correntes calculadas nos itens (a) e (b), qual é a maior? Justifique sucintamente o fato de uma corrente ser maior que a outra.

Passo 1

a) Para resolvermos os dois primeiros itens, vamos dar uma olhada para a figura abaixo, que mostra apenas a seção transversal atravessada pela corrente I , que é perpendicular à página e está saindo dela, na direção e sentido de + z ^ .

Neste caso, podemos escrever o vetor área como

d A → = 2 π r d r + z ^ ,

cujo módulo obtivemos considerando o elemento de área mostra na figura acima. Essa é a área atravessa pela corrente I , cujo vetor densidade de corrente é   J → = J 0 r R ( + z ^ ) . Portanto,   d A → e   J → são paralelos e vamos usar isso também para matar o item b depois.

Como  J → é uma densidade superficial de corrente, ou seja, é uma grandeza que dá a quantidade de corrente por unidade de área, a corrente I é escrita como:

I = ∫ S J → ⋅ d A →   ,

que é a integral do produto escalar entre   J → e   d A → . Nesse caso, como  d A → e  J → são paralelos, I fica

I = ∫ J 0 r R   ( 2 π r d r ) = 2 π J 0 R   ∫ 0 R r 2 d r     ⇒     I   =   2 π J 0 R 2 3 = I a .

Passo 2

b) Aqui, vamos substituir a outra expressão para J :

I = ∫ J 0 1 - r R ( 2 π r d r ) = 2 π J 0 ∫ 0 R r d r - 1 R ∫ 0 R r 2 d r = 2 π J 0 R 2 2 - 1 R R 3 3   ,

que simplificada tem esta outra “cara”:

I = π J 0 R 2 3 = I b .

Passo 3

c) A corrente I a do item a) é maior do que a I b do item b): I a = 2 I b . Isso acontece porque a densidade de corrente no item a) aumenta linearmente com a distância r a partir do centro, ou seja, à medida que área atravessada pela corrente aumenta, a quantidade de corrente que atravessa essa área também aumenta resultando em uma corrente total I maior.

Já no caso do item b), a densidade de corrente diminui linearmente com r , o que significa que à medida que área pela qual a corrente passa aumenta, a quantidade de corrente diminui, o que dá, no final das contas, uma corrente total I menor.

Resposta

  1. I   =   2 π J 0 R 2 3 = I a   ;
  2. I   =   π J 0 R 2 3 = I b   ;
  3. I a = 2 I b > I b , pois a densidade de corrente no item a) aumenta com r e a do item b) diminui com r à medida que a área aumenta.

Exercício Resolvido #5

Usp - Física 3 – P2 2018.1 -1(letra A)

Considere um fio retilíneo muito longo de raio R e centrado ao longo do eixo z no qual passa uma corrente estacionária I (ao longo da direção z ), conforme mostra a figura abaixo. A corrente elétrica é distribuída de forma que sua densidade de corrente é dada por:   J → r = C r   k ^ (se 0 ≤ r ≤ R ), e 0 caso contrário, sendo C > 0 uma constante.

  1. Determine a corrente total I em função de C e R .

Passo 1

a) Precisamos nos lembrar aqui que o elemento de corrente d I atravessando o elemento de área d A relaciona-se com a densidade de corrente   J → ( r ) de acordo com

d I = J → r ⋅ d A →   ,

que é o produto escalar dos vetores   J → ( r ) e  d A → . A direção e sentido de  J → ( r ) o problema já deu para gente e agora temos que ver como fica  d A → . Para isso, vamos olhar a figura abaixo, que mostra o desenho do perfil do cilindro acima.

Nessa figura, colocamos vetor  d A → saindo do plano da página na mesma direção e sentido de   J → ( r ) , ou seja,   d A → = 2 π r d r   k ^ . Portanto, nesse caso temos que a corrente total I é:

I = ∫ 0 R J → ⋅ d A → = ∫ 0 R J r d A = 2 π C ∫ 0 R r 2 d r ⇒ I = 2 π C 3 R 3   .

Resposta

  1. I = 2 π C 3 R 3   ;

Exercício Resolvido #6

Instituto de Física Gleb Wataghin

A densidade de corrente em um fio cilíndrico de raio R = 2,0   m m varia com a distância radial r segundo J = a r ² , onde a = 3 × 10 11   A / m 4 e r está em metros. Qual a corrente que atravessa a porção externa do fio entre as distâncias radiais R / 2 e R ?

Passo 1

Pra resolver esse exercício, vamos usar a relação J = i A , onde A , nesse caso, vai ser π R 2 - R 2 2 , já que ele quer a corrente na região entre R 2 e R .

Então

A = π ( 2 × 10 - 3 2 - 10 - 3 2 )

A = 9,4 × 10 - 6   m ²

Agora é só substituir na fórmula pra achar i :

i = ∫ R / 2 R J d A

i = 9,4 × 10 - 6 ∫ R / 2 R 3 × 10 11 × r 2 d r

i = 9,4 × 10 - 6 × 3 × 10 11 R 3 3 - R 3 8 3

i = 9,4 × 10 - 6 × 3 × 10 11 7 R 3 24

i = 0,00658   A

Resposta

i = 0,00658   A

Exercícios de Livros Relacionados

A relação corrente-voltagem para um diodo semicondutor é dada por I = I S exp ⁡ e V k T - 1 Em que V é a voltagem nos terminais do diodo, I é a corrente que flui através do diodo, I S é uma constante
Determine a corrente em um fio de raio R = 3,40 m m se o módulo da densidade de corrente é dado por (a) J a = J 0 R e (b) J b = J 0 ( 1 - r / R ) , onde r é a distância radial e J 0 = 5,50 × 10 4 A /
Três esferas pequenas x,y e z, possuem cargas de mesmo módulo e os sinais indicados. Elas estão localizadas nos vértices de um triangulo isósceles, sendo a distância entre x e y igual a distância entr
Quanto tempo os elétrons levam para ir da bateria de um carro até o motor de arranque? Suponha que a corrente é 300A e que o fio de cobre que liga a bateria ao motor de arranque tem 0,85m de comprimen
Um ser humano pode morrer se uma corrente elétrica da ordem de 50m A passar perto do coração. Um eletricista trabalhando com as mãos suadas, o que reduz consideravelmente a resistência da pele, segura