Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Densidade de Corrente

Ver Todos os Exercícios

Teoria

A densidade de corrente é um vetor do fluxo de cargas através da seção reta de um condutor em um certo ponto. Se liga na imagem abaixo:

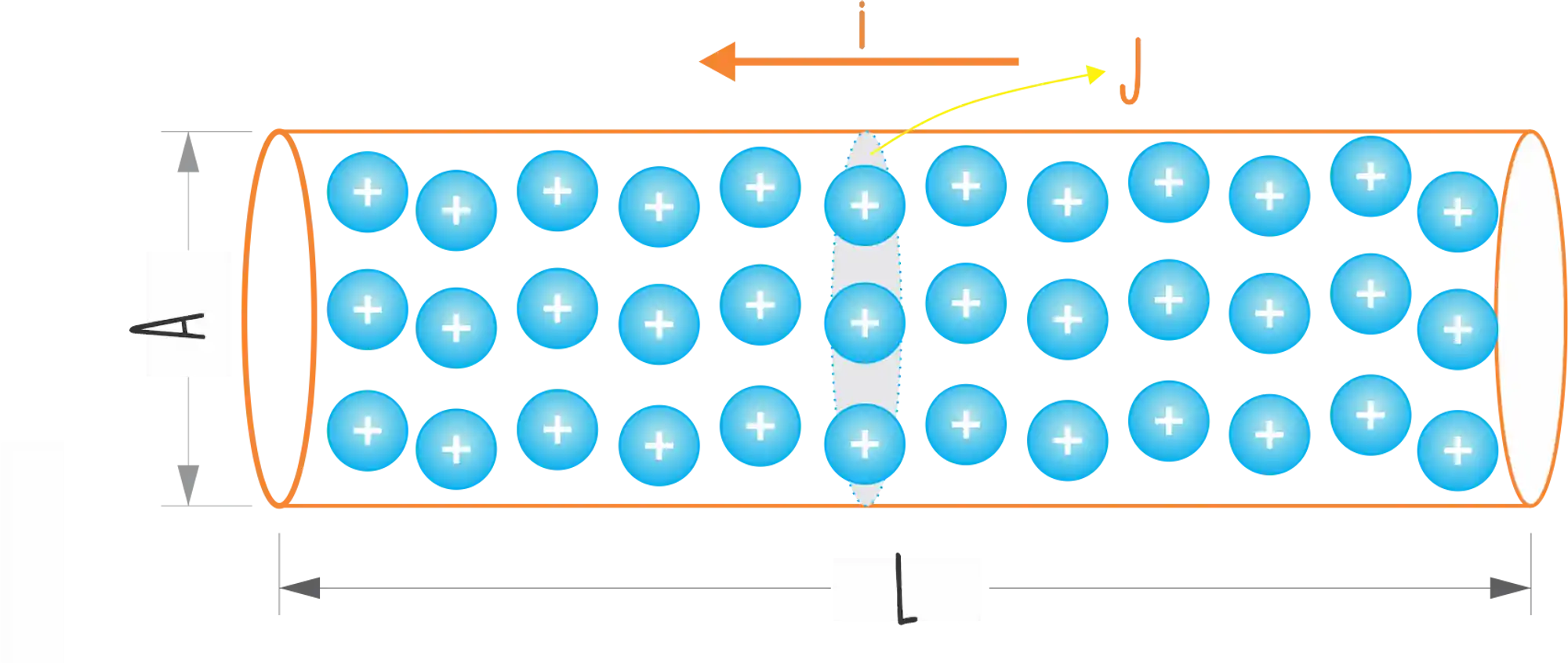
Densidade de Corrente Elétrica
Densidade de Corrente Elétrica

Temos um fluxo de cargas uniformes passando pelo fio, que é a nossa corrente , se a gente pegar um filetinho da secção transversal do fio e contar quantas cargas tem ali. Essa vai ser nossa densidade de corrente elétrica! 🤩

Então a densidade de corrente pode ser calculada por:

Onde é o vetor unitário que dá a direção do fluxo da corrente. A densidade de corrente aponta na direção e no sentido que flui a corrente. Lembrando que o sentido da corrente era dado pelo sentido do fluxo das cargas positiva!

📢 Clique para saber mais:

Densidade de Corrente Uniforme

Imagine um fio de seção transversal circular conduzindo uma determinada corrente elétrica . Se a corrente for uniformemente distribuída ao longo da seção reta, a densidade de corrente será dada por:

Aqui estamos falando de um fio condutor, então a área de sua secção transversal é a área de uma circunferência:

A corrente elétrica variará, com o raio da seguinte forma:

Se analisarmos um gráfico da corrente em função de , veremos que o coeficiente angular da reta será .

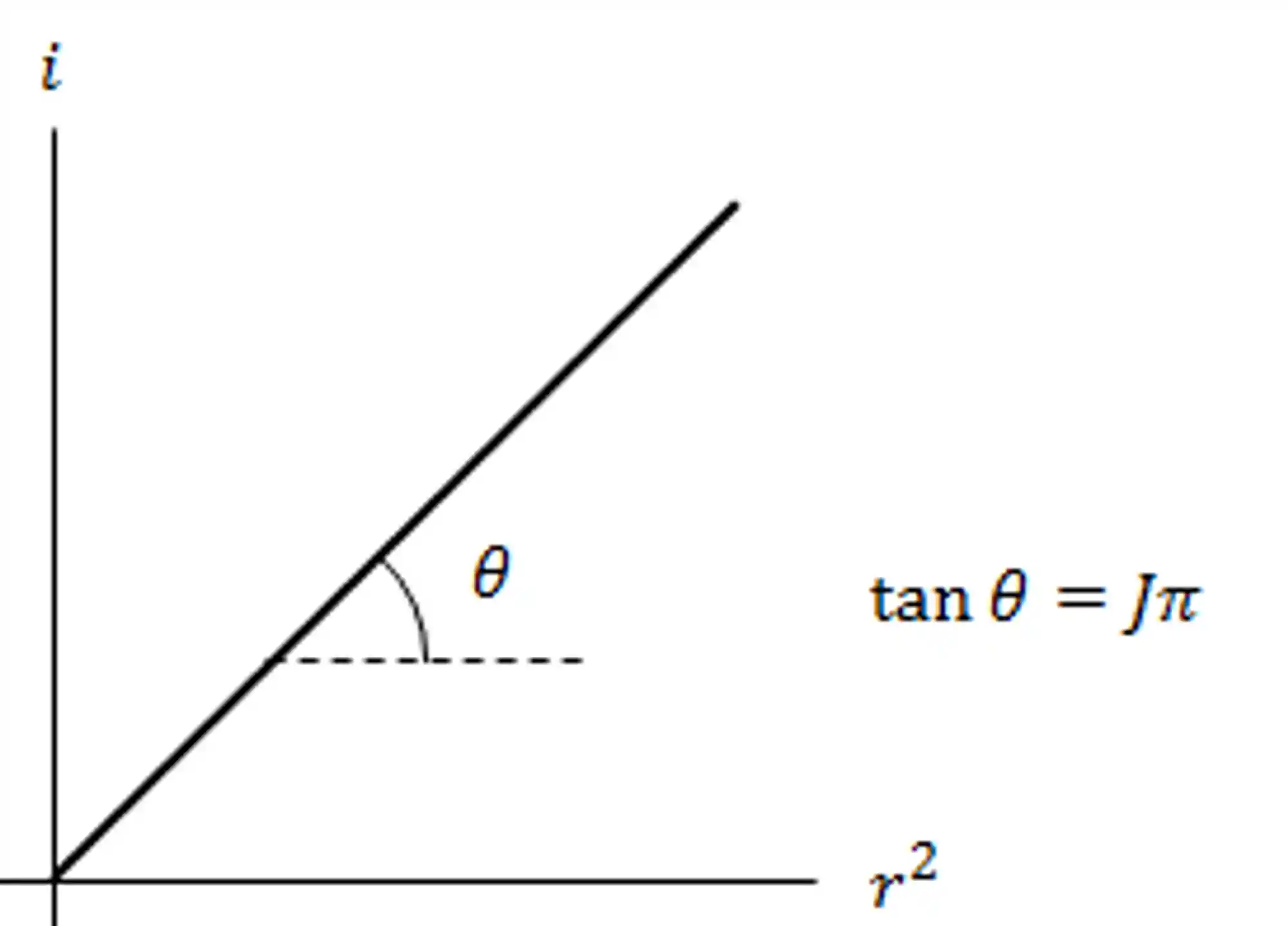
Variação da corrente elétrica em função do raio do fio
Variação da corrente elétrica em função do raio do fio

Você também pode conferir esse conteúdo em vídeo:

Velocidade de Deslocamento dos Elétrons: A Velocidade de Deriva

A corrente elétrica é o fluxo de cargas, ou seja ela nos diz a quantidade de cargas elétricas que passam por tempo. Podemos então calcular a velocidade de deriva , isso é, a velocidade média de deslocamento dos elétrons usando a corrente elétrica e a densidade de cargas!

Se é a quantidade de carga que passa no condutor em um determinado intervalo de tempo, podemos escrever o seguinte:


Onde é a quantidade total de elétrons e é a carga elementar (carga de um elétron). Vamos imaginar os elétrons percorrendo um fio de cobre:

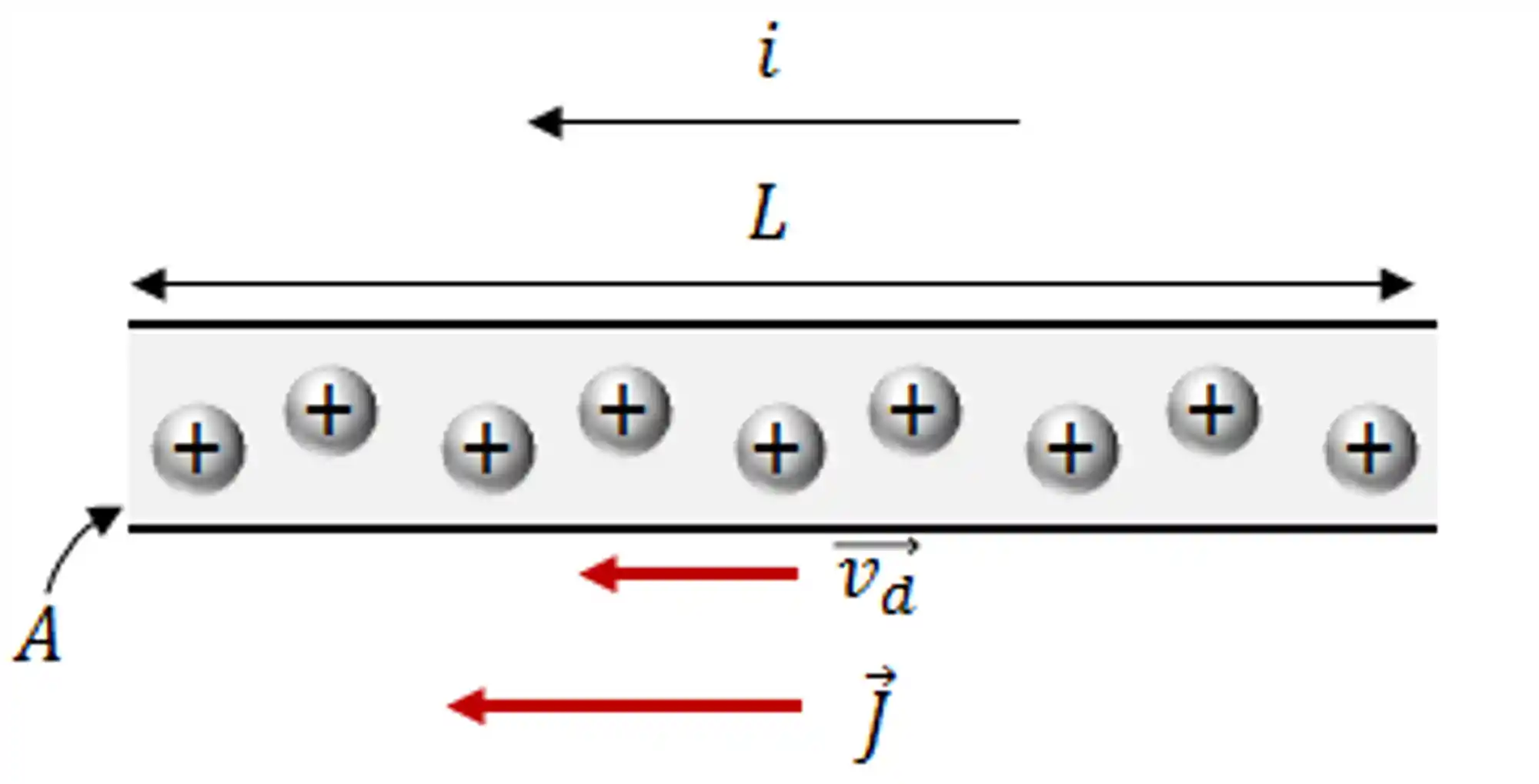
Corrente elétrica em um fio
Corrente elétrica em um fio

Nesse caso, podemos dizer que o número de cargas que cabem em um pedaço de fio é , onde é o número de elétrons por unidade de volume e é a área da seção transversal.

A velocidade com que os elétrons atravessam esse mesmo pedaço de fio é:

Substituindo na fórmula de corrente:

Isolando :

Substituindo a densidade de corrente, ficamos com:

Prontinho, temos a fórmula da velocidade de deriva para os elétrons! Vamos praticar com exercícios?

Velocidade de Deslocamento dos Elétrons: A Velocidade de Deriva

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria.

Uma corrente de 3 × 10 - 9   A atravessa um fio de cobre. Considerando que a densidade de corrente vale 4,5 × 10 - 5   A / m ² , calcule a área do fio.

Passo 1

Nesse probleminha, vamos usar a relação A = i J , é só substituir:

A = 3 × 10 - 9 4,5 × 10 - 5

A = 66,6 × 10 - 6   m ²

Resposta

A = 66,6 × 10 - 6   m ²

Exercício Resolvido #2

Elaboração própria.

Suponha um fio de cobre com seção reta de 0,25   c m ² . Considerando um ponto A e um ponto B nesse fio, separados por uma distância de 1   m e que os elétrons levam 5 minutos para irem do ponto A até o ponto B , qual a corrente que passa pelo fio?

Considere que o número de portadores de carga por unidade de volume é 9 × 10 27   m - 3 .

Passo 1

Antes de tudo, vamos descobrir qual a velocidade de deriva, lembrando que 5 minutos equivalem a 300 segundos:

v d = 1   m 300   s

v d = 3,33 × 10 - 3   m / s

Passo 2

Agora, basta substituir v d na expressão v d = i n A e para encontrarmos i , mas antes vamos converter as unidades belezinha?

A = 0,25   c m 2 = 2,5 × 10 - 5   m ²

Substituindo na fórmula:

i = 3,33 × 10 - 3 × 9 × 10 27 × 2,5 × 10 - 5 × 1,6 × 10 - 19

i = 119,88   A

Resposta

i = 119,88   A

Exercício Resolvido #3

UFRJ , P1 2014.1, Múltipla Escolha n° 5

Uma corrente é estabelecida num tubo de descarga de gás quando uma diferença de potencial (ddp) é aplicada entre dois eletrodos no tubo. O gás se ioniza, os elétrons movem-se em direção ao terminal positivo e os íons positivos em direção ao terminal negativo. Em um tubo de descarga de hidrogênio, 7,00 × 10 18 elétrons e 3,00 × 10 18 prótons passam através da seção reta do tubo a cada segundo. Quais são o módulo I da corrente elétrica e o sentido do vetor densidade de corrente elétrica nesse tubo de descarga? Lembre-se que o módulo da carga do elétron vale 1,60 × 10 - 19 C .

  1. I = 1,60   A . Sentido: do terminal positivo para o negativo.
  2. I = 0,640   A . Sentido: do terminal positivo para o negativo.
  3. I = 1,60   A . Sentido: do terminal negativo para o positivo.
  4. I = 0,640   A . Sentido: do terminal negativo para o positivo.
  5. I = 1,12   A . Sentido: do terminal positivo para o negativo.
  6. I = 1,12   A . Sentido: do terminal negativo para o positivo.

Passo 1

Primeiramente, desenhamos:

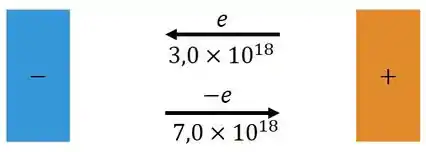
Beleza. Como temos prótons pra um lado e elétrons pro outro de corrente, o número de partículas total nada mais é do que a soma dos dois:

n = 7 + 3 × 10 18

n = 10 × 10 18

n = 10 19

Passo 2

Dado que temos o número de partículas, e a carga do elétron e do próton são iguais em módulo, temos que a carga total é:

Q = 10 19 × 1,6 × 10 - 19 C

Q = 1,6   C

Isso funciona porque os elétrons e prótons em movimento estão indo em sentidos opostos. Portanto eles se somam para gerar a corrente total.

Um elétron indo da esquerda pra direita gera a mesma corrente que um próton indo da direita pra esquerda.

Passo 3

Como o enunciado diz que essa é a carga que cruza uma seção reta do fio a cada segundo, temos:

I = Q Δ t

I = 1,6 C s

I = 1,6   A

Passo 4

O vetor densidade de corrente nada mais é que:

J → = I A s ^

Onde I e A estão em módulo e s ^ é o vetor que dá o sentido e a direção da corrente. Como a corrente tem o sentido contrário ao dos elétrons, e eles seguem em direção ao terminal positivo, temos que o sentido dela é do positivo pro negativo.

Logo...

Resposta

Letra a

Exercício Resolvido #4

Instituto de Física Gleb Wataghin

A densidade de corrente em um fio cilíndrico de raio R = 2,0   m m é uniforme em uma seção transversal do fio e vale J = 2,0 × 10 5   A / m ² . Qual a corrente que atravessa a porção externa do fio entre as distâncias radiais R / 2 e R ?

Passo 1

Pra resolver esse exercício, vamos usar a relação J = i A , onde A , nesse caso, vai ser π R 2 - R 2 2 , já que ele quer a corrente na região entre R 2 e R .

Então

A = π ( 2 × 10 - 3 2 - 10 - 3 2 )

A = 9,4 × 10 - 6   m ²

Agora é só substituir na fórmula pra achar i :

i = J A

i = 2,0 × 10 5 × 9,4 × 10 - 6

i = 1,88   A

Resposta

i = 1,88   A

Exercício Resolvido #5

Halliday/ Resnick, Fundamentos da Física Volume 3, 8ª ed. LTC, Cap. 26, pp. 160-4

Uma corrente pequena, porém mensurável, de 1,2 × 10 - 10 A atravessa um fio de cobre de 2,5 m m de diâmetro. O número de portadores de carga por unidade de volume é 8,49 × 10 28   m - 3 .

Supondo que a corrente é uniforme, calcule a a densidade de corrente e b a velocidade de deriva dos elétrons.

Passo 1

a Calcule a densidade de corrente;

Por definição, a densidade de corrente é dada por:

J = i A

Como a seção reta do fio é circular, a área transversal será:

A = π r 2 = π d 2 4

Onde d = 2,5   m m = 2,5 × 10 - 3 m .

Substituindo os valores, teremos:

J = i π d 2 4 = 4 i π d 2

J = 4 × 1,2 × 10 - 10 π × 2,5 × 10 - 3 2

J = 2,4 × 10 - 5   A / m 2

Passo 2

b Calcule a velocidade de deriva dos elétrons;

A velocidade de deriva está associada à densidade de corrente através da expressão:

v d = J n e

Onde n é a quantidade de portadores de carga por unidade de volume e vale 8,49 × 10 28   m - 3 , e e é a carga elementar que vale e = 1,6 × 10 - 19 C .

Logo:

v d = 2,4 × 10 - 5 8,49 × 10 28 × 1,6 × 10 - 19

v d = 1,8 × 10 - 15   m / s

Resposta

a

J = 2,4 × 10 - 5   A / m 2

b

v d = 1,8 × 10 - 15   m / s

Exercício Resolvido #6

Halliday/ Resnick, Fundamentos da Física Volume 3, 8ª ed. LTC, Cap. 26, pp. 160-5

O fusível de um circuito elétrico é um fio projetado para fundir, abrindo o circuito, se a corrente ultrapassar um certo valor.

Suponha que o material a ser usado em um fusível funde quando a densidade de corrente ultrapassa 440   A / c m 2 . Que diâmetro de fio cilíndrico deve ser usado para fazer um fusível que limite a corrente a 0,50   A ?

Passo 1

O problema nos deu a densidade de corrente e a corrente máxima... agora já podemos nos virar sozinhos.

A densidade de corrente é dada por:

J = i A

Como a seção reta do fio é circular, a área transversal será:

A = π r 2 = π d 2 4

Substituindo na expressão da densidade de corrente, teremos:

J = 4 i π d 2

Reorganizando essa expressão, teremos:

d = 4 i π J

Agora é partir pros cálculos.

Passo 2

A corrente é dada por:

i = 0,50   A

E a densidade de corrente é dada por:

J = 440 A c m 2 = 440 A 10 - 2 m 2

J = 440 10 - 4 A m 2

J = 4,4 × 10 6 A m 2

Agora sim, substituindo na expressão de d , teremos:

d = 4 i π J

d = 4 × 0,5 π × 4,4 × 10 6

d = 3,8 × 10 - 4   m

d = 0,38   m m

Resposta

d = 0,38   m m

Exercício Resolvido #7

Halliday/ Resnick, Fundamentos da Física Volume 3, 8ª ed. LTC, Cap. 26, pp. 160-9

Quanto tempo os elétrons levam para ir da bateria de um carro até o motor de arranque?

Suponha que a corrente é de 300   A e que o fio de cobre que liga a bateria ao motor de arranque tem 0,85   m de comprimento e uma seção reta de 0,21   c m 2 .

O número de portadores de carga por unidade de volume é 8,49 × 10 28 m - 3 .

Passo 1

Nós temos a distância entre a bateria e o motor de arranque, então, se descobrirmos a velocidade de deriva, podemos calcular o tempo que os elétrons levam nessa trajetória.

A velocidade de deriva é dada por:

v d = i n A e

Onde:

i = 300   A

n = 8,49 × 10 28 m - 3

A = 0,21   c m 2 = 2,1 × 10 - 5   m 2

e = 1,6 × 10 - 19 C

Logo:

v d = 300 8,49 × 10 28 × 2,1 × 10 - 5 × 1,6 × 10 - 19

v d = 1,05 × 10 - 3   m / s

Passo 2

O tempo necessário para os elétrons irem da bateria ao motor de arranque será:

v d = Δ s Δ t → Δ t = Δ s v d

Δ t = 0,85 1,05 × 10 - 3

Δ t = 809,52   s

Δ t = 13,5   m i n

Resposta

Δ t = 13,5   m i n

Exercício Resolvido #8

Young & Freedman, Física III Eletromagnetismo, 14ª ed. Pearson, Cap. 25, pp.172

O cobre contém 8,5 × 10 28 elétrons livres por metro cúbico. Um fio de cobre com calibre 12 , que possui diâmetro de 2,05   m m e comprimento de 71,0   c m , conduz uma corrente elétrica igual a 4,85   A .

(a) Qual é o tempo necessário para um elétron percorrer o comprimento do fio?

(b) Repite a parte (a) para um fio de cobre com calibre 6 (diâmetro igual a 4,12   m m ) com o mesmo comprimento e conduzindo a mesma corrente.

(c) De modo geral, como a variação do diâmetro de um fio altera a velocidade de arraste dos elétrons no fio?

Passo 1

(a) Qual é o tempo necessário para um elétron percorrer o comprimento do fio?

Vamos começar a resolver essa questão calculando a densidade de corrente. A gente sabe que, por definição:

J = I A = I π r 2 ,

J = 4,85 π 1,025 × 10 - 3 2 ≈ 1,5 × 10 6   A / m 2 .

Passo 2

Com isso, a gente consegue calcular a velocidade de arraste, que é dada por:

v d = J n e ,

v d = 1,5 × 10 6 8,5 × 10 28 × 1,6 × 10 - 19 ≈ 1,1 × 10 - 4   m / s .

Passo 3

O tempo necessário para um elétron percorrer o comprimento L do fio vai ser dado por:

t = L v d ,

t = 71 × 10 - 2 1,1 × 10 - 4 ≈ 64,5 × 10 2   s .

Passo 4

(b) Repite a parte (a) para um fio de cobre com calibre 6 (diâmetro igual a 4,12   m m ) com o mesmo comprimento e conduzindo a mesma corrente.

Vamos lá: aqui precisamos repetir os passos acima para um novo diâmetros.

Então, a nova densidade de corrente será:

J = 4,85 π 2,06 × 10 - 3 2 ≈ 3 , 6 × 10 5   A / m 2 .

A nova velocidade de arraste será:

v d = 3,6 × 10 5 8,5 × 10 28 × 1,6 × 10 - 19 ≈ 2,6 × 10 - 5   m / s .

E, por fim, o novo tempo será

t = 71 × 10 - 2 2,6 × 10 - 5 ≈ 27,3 × 10 3   s .

Passo 5

(c) De modo geral, como a variação do diâmetro de um fio altera a velocidade de arraste dos elétrons no fio?

A gente consegue perceber pela fórmula da velocidade de arraste que ela é proporcional à densidade de corrente. Assim sendo, ela será inversamente proporcional ao quadrado do diâmetro do fio. Isso significa que que se a gente aumentar o diâmetro por um fator qualquer, a velocidade de arraste vai diminuir com o quadrado desse mesmo fator ;)

Resposta

(a) t = 64,5 × 10 2   s .

(b) t = 27,3 × 10 3   s .

Exercícios de Livros Relacionados

Um fio de cobre de calibre 10 conduz uma corrente de 20A . Considerando que o cobre tenha um elétron livre por átomo, calcule a rapidez de deriva dos elétrons livres no fio.
Uma corrente pequena, porém mensurável, de 1,2 × 10 - 10 A atravessa um fio de cobre de 2,5 m m de diâmetro. O número de portadores de carga por unidade de volume é 8,49 × 10 28 m - 3 . Supondo que a
O fusível de um circuito elétrico é um fio projetado para fundir, abrindo o circuito, se a corrente ultrapassar um certo valor. Suponha que o material a ser usado em um fusível funda quando a densidad
Um pedaço de fio de cobre calibre 10 e um pedaço de fio de cobre calibre 14 estão soldados entre si nas duas extremidades. Os fios conduzem uma corrente de 15A . (a) Se há um elétron livre para cada á
Em um dos feixes que colidem em um supercolisor de prótons, os prótons estão se movendo com velocidades aproximadamente iguais à velocidade da luz e a corrente do feixe é 5,00m A . A densidade de corr