Equilíbrio Estático em Corpos de Mais de uma Dimensão
Produzido por Ludovic BeghinTeoria
Equilíbrio Estático em Corpos de mais de uma dimensão
Esse assunto é bem parecido com os anteriores, só vamos ter alguns cuidados específicos.
É lógico que como se trata de equilíbrio estático as condições de equilíbrio vão continuar valendo!
- o somatório das forças externas ser zero
- o somatório dos torques externos em relação a qualquer ponto ser zero
Vamos lá!
Imagina que somos engenheiros... Um dia seremos!
![]()
E recebemos uma vista de cima com as forças de um projeto. Precisamos verificar se a vista está em equilíbrio estático.
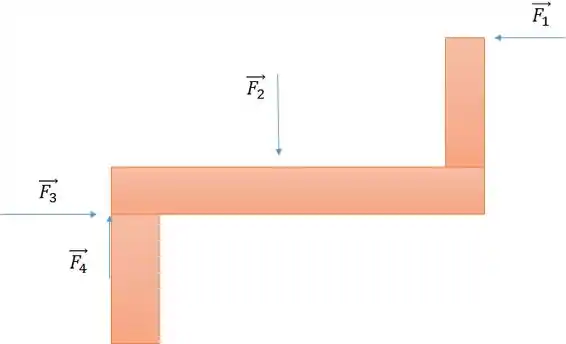
Somatório de Forças Externas
Nesse tipo de questão, vamos fazer um eixo e simplesmente fazer o somatório de e .
Muito parecido com os exercícios de um dimensão só!
No exemplo da vista, teríamos:
Tranquilo!
Somatório dos Torques Externos
Aqui a lógica é bem parecida com as questões de barras unidimensionais.
Precisamos achar as distâncias perpendiculares dos eixos de rotação até as linhas de ação da força.
Vamos ver no exemplo!
No exemplo da figura, o melhor eixo que poderíamos escolher é o ponto de encontro entre e , pois aí só teremos torque gerado por e .
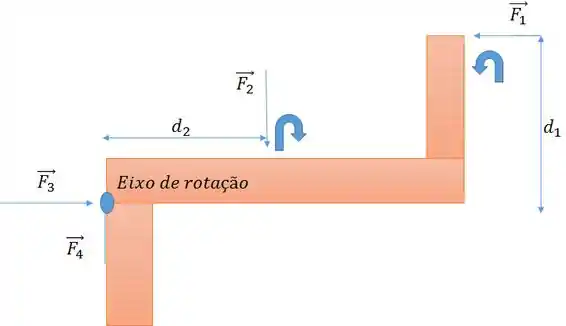
Achando as distâncias e e utilizando o sentido anti-horário como positivo, posso montar a equação.
Show!
Vou mostrar agora alguns detalhezinhos que, às vezes, vai ser necessário saber.
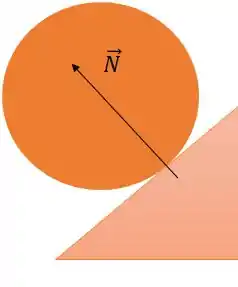
Ponto que a normal age
Em vários problemas desse tipo, será necessário saber definir o ponto em que a força normal age sobre o corpo.
É sempre no ponto de contato entre a superfície e o corpo!
Repare na figura abaixo!
Centro de gravidade
É preciso ter um pouco de atenção na análise dos centros de gravidade de alguns corpos também.
Normalmente ele está no centro de massa!
Aqui vão alguns exemplos:
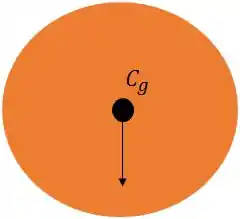
O centro de gravidade da esfera é localizando em seu ponto central
O centro de gravidade de um cubo ou paralelepípedo é localizado em seu ponto central
Show!
É isso que vai ser cobrado nos exercícios! Vamos resolver?
Somatório de Forças Externas
Somatório dos Torques Externos
Ponto que a normal age
Centro de gravidade
Exercícios Resolvidos
Exercício Resolvido #1
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 12, pp 18-5
Na figura abaixo, uma esfera uniforme de massa e raio é mantida em repouso por uma corda de massa desprezível, presa a uma parede sem atrito a uma distância acima do centro da esfera.
Determine
- A tensão da corda
- A força que a parede exerce sobre a esfera

Passo 1
Vamos montar o problema.
Temos
a força normal
o peso da bola
a tração
o ângulo que a tração faz com a parede
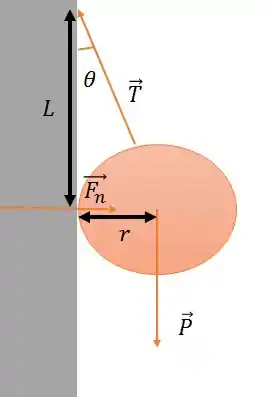
Passo 2
Podemos descobrir o valor desse ângulo, já que temos os dois catetos de um triângulo retângulo e r.
Passo 3
Então, podemos aplicar as condições de equilíbrio.
Vamos aplicar
Para isso, temos que decompor em e .
Pela figura, aplicando decomposição de vetores, vemos que
, repare que o sentido está negativo
Então,
Passo 4
Vamos resolver as equação.
Vou começar pela
Passo 5
Agora aplcamos na equação:
Resposta
Exercício Resolvido #2
Paul A. Tipler e Gene Mosca, Física Para Cientistas e Engenheiros Volume 1, 6ª edição, Cap 12, pp 424 - 21
Um cilindro de massa está apoiado sobre uma calha sem atrito, formada por um plano inclinado de com a horizontal, à esquerda, e outro plano inclinado de , à direita, como mostrado na figura abaixo. Determine a força exercida por cada plano sobre o cilindro.
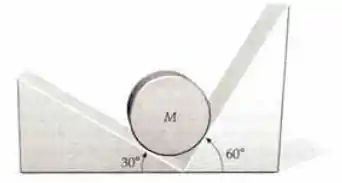
Passo 1
Vamos começar montando a figura. Temos um cilindro entre dois planos inclinados sem atrito.
É possível perceber que tem duas forças normais e a força peso do cilindro, conforme mostra a figura abaixo:
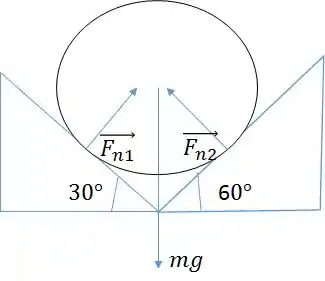
Passo 2
Como a situação é de equilíbrio, vamos usar as condições de equilíbrio:
Mas antes disso, temos que decompor e .
A ideia é descobrir a inclinação dessas forças. Montamos, então, a seguinte figura:
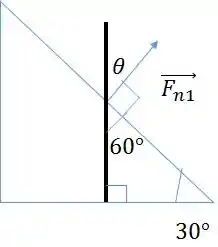
Perceba que descobrindo o valor de , podemos decompor em e .
Montando esse triângulo, fica fácil de ver que .
De forma análoga, no plano de , temos a seguinte figura:
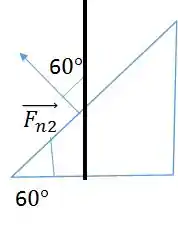
Show! Agora já podemos decompor as forças (lembre-se cosseno lado colado ao ângulo e seno lado oposto) e utilizar as equações.
Passo 3
Começando por:
Agora podemos utilizar a outra equação:
Substituindo o valor de :
Podemos agora descobrir o valor de :
Resposta
Exercício Resolvido #3
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 12, pp 19-13
As forças agem sobre a estrutura cuja vista superior aparece na figura abaixo. Deseja-se colocar a estrutura em equilíbrio aplicando uma quarta força em um ponto como P. A quarta força tem componentes vetoriais e . Sabe-se que , , , , , .
Determine
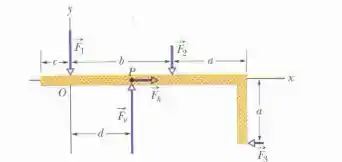
Passo 1
Vamos começar analisando .
Podemos usar uma das equações do equilíbrio estático:
Passo 2
Para analisar , vamos usar outra equação do equilíbrio estático.
Passo 3
Para descobrirmos , vamos utilizar a equação referente ao torque.
Escolhendo o ponto O como eixo de rotação, montamos a seguinte equação:
Resposta
Exercício Resolvido #4
Paul A. Tipler e Gene Mosca, Física Para Cientistas e Engenheiros Volume 1, 6ª edição, Cap 12, pp 429 - 72
Uma esfera homogênea, de raio e massa , é mantida em repouso, por um cordão horizontal, sobre um plano inclinado de ângulo , como mostrado na figura abaixo. Seja .
- Qual é a tração no cordão?
- Qual é a força normal exercida sobre a esfera pelo plano inclinado?
- Qual é a força de atrito atuando sobre a esfera?
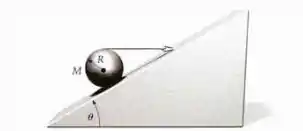
Passo 1
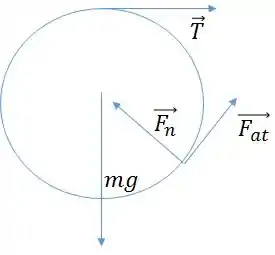
Primeiro, vamos marcar as forças que atuam na figura.
: Força normal, perpendicular à superfície
: Tração da corda
: Força de atrito
: Força peso
Conforme mostra a figura abaixo:
Passo 2
Vamos agora analisar as equações de equilíbrio. Mas antes disso, vamos mudar o eixo para a seguinte forma:
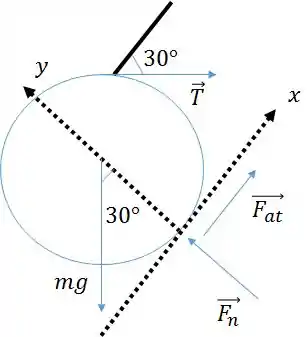
Por que isso?
Nossa análise vai ficar mais simples.
Já temos o ângulo de inclinação das forças e e podemos achar a decomposição desses vetores facilmente utilizando o ângulo ( lembre-se de cosseno é o lado colado ao ângulo e seno o lado oposto).
Passo 3
Agora que montamos o diagrama de forças, podemos aplicar as condições de equilíbrio.
Vamos começar aplicando para um eixo de rotação no centro da esfera. Dessa forma, sabemos que os momentos gerados por e são zeros.
Perceba que a distância do centro da esfera (eixo de rotação) até a linha de atuação das forças e vale . Essa distância também é perpendicular à linha de ação das duas forças. Assim, podemos aplicar, escolhendo o sentido anti-horário como positivo:
Passo 4
Vamos agora aplicar as outras condições de equilíbrio estático. Mas, antes disso, vamos decompor as forças necessárias.
Lembrando que mudamos os eixos tradicionais lá em cima para a análise ficar mais simples.
Sendo assim, está no eixo e no eixo e precisamos achar as componentes das forças e .
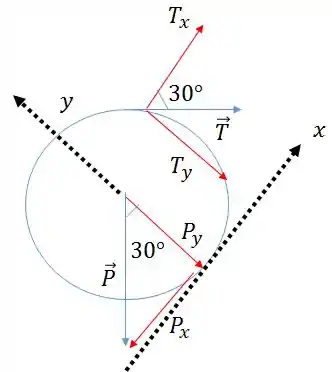
Agora ficou mais tranquilo fazer essa decomposição:
Passo 5
Agora podemos aplicar as outras condições de equilíbrio estático.
Vamos começar por para descobrirmos .
Como :
Passo 6
Vamos aplicar agora para descobrirmos .
Passo 7
Pela equação de momento que aplicamos no passo 3, sabemos que:
Resposta
Exercício Resolvido #5
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 12, pp 24-58
Na figura abaixo, duas esferas idênticas uniformes e sem atrito, de massa m, respousam em um recipiente retangular rígido. Uma reta que liga os centros das esferas está a com a horizontal. Determine o módulo das forças exercidas sobre as esferas:
- pelo fundo do recipiente
- pela parede lateral esquerda do recipiente
- pela parede lateral direita do recipiente
- por uma das esferas sobre a outra.
(Sugestão: A força de uma esfera sobre a outra aponta ao longo da reta que passa pelo centro)
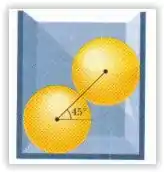
Passo 1
Vamos primeiro marcar as forças.
Temos:
: A força que a parede direita exerce sobre a esfera
: A força que a parede esquerda exerce sobre a esfera
: O peso da bola
: A força normal do chão na bola debaixo
: A força de contato entre as duas esferas
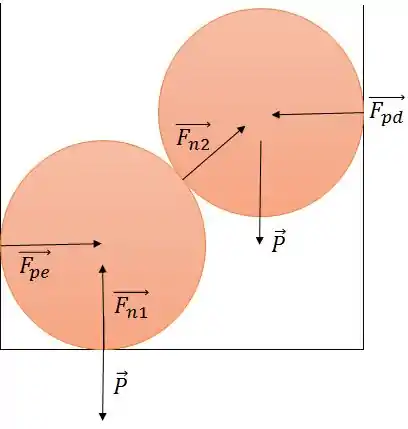
Passo 2
Agora, vamos decompor em e para podermos aplicar as condições de equilíbrio.
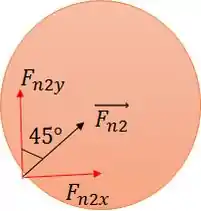
Podemos ver pela figura acima que
Passo 3
Agora, podemos aplicar as condições de equilíbrio para descobrirmos a força , ou seja, a força normal do chão na bola debaixo. Para isso, vamos analisar as duas esferas como um único bloco.
Quando analisamos as duas esferas juntas, pela terceira lei de newton (ação e reação), a vai se anular com uma força de mesmo módulo e sentido oposto exercida sobre a esfera debaixo pela esfera de cima.
Assim, vamos utilizar a condição de equilíbrio: .
Como só temos as duas forças peso para baixo e para cima.
Passo 4
Vamos calcular primeiro a força que a parede exerce na bola direita. Para isso vamos analisa-la separadamente.
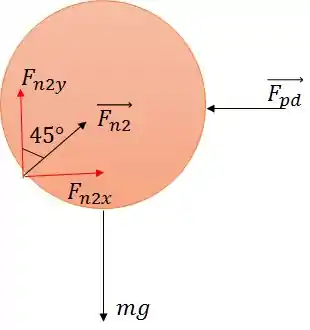
Vemos por que
Logo, podemos descobrir
Aplicando
Passo 5
Para analisar a força da parede esquerda, podemos analisar as duas esferas juntas. Lembrando que quando analisamos as duas juntas a forças de ação e reação de uma esfera sobre a outra se anulam.
Assim, aplicando
Passo 6
A força de uma esfera sobre a outra já foi achada no passo 4
Como
Então,
Resposta
Exercício Resolvido #6
Paul A. Tipler e Gene Mosca, Física Para Cientistas e Engenheiros Volume 1, 6ª edição, Cap 12, pp 430 - 74
A figura abaixo mostra uma prancha homogênea de de comprimento, sobre um cilindro de de raio. A massa da prancha é e a do cilindro . O coeficiente de atrito estático entre a prancha e o cilindro é zero, enquanto os coeficientes de atrito estático entre o cilindro e o piso, e entre a prancha e o piso, não são nulos. Existem valores, para estes coeficientes de atrito estático, para os quais o sistema fique em equilíbrio estático? Caso afirmativo, que valores são esses? Caso negativo, explique o porquê de sua não existência.
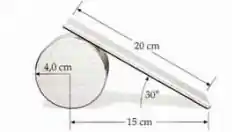
Passo 1
Vamos primeiro montar o diagrama das forças do problema.
Se liga!
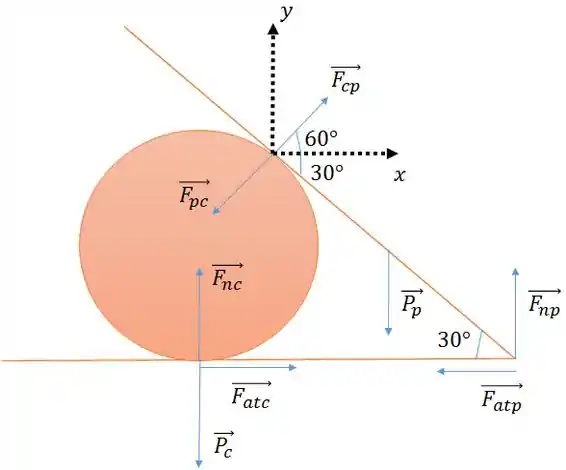
Calma! Ficou confuso, né? Vou explicar cada coisa.
é a força normal que o chão exerce na prancha
é a força normal que o chão exerce no cilindro
é a força de atrito na prancha
é a força de atrito no cilindro
é o peso da prancha, localizado em seu centro de massa
é o peso do cilindro, localizado em seu centro de massa
é a força que a prancha exerce no cilindro
é a força que o cilindro exerce na prancha
Por serem forças de ação e reação, elas são iguais:
Muitas forças, né? Isso é chatinho. Mas isso acontece porque são dois corpos encostados no chão. Então temos peso, normal e atrito para cada um.
Não podemos esquecer do ângulo fornecido. Podemos descobrir a inclinação de .
Primeiro utilizamos uma transversal cortando duas retas paralelas: ângulos alternos internos são iguais!
Depois, utilizamos o fato de que a força é perpendicular a superfície. Logo, o ângulo é de .
Muita coisa, né? Mas já é um adianto enorme no problema.
Passo 2
Como o enunciado pede uma relação dos coeficientes de atrito, vamos escrevê-los na forma das forças acima. Lembre-se que .
Vamos achar:
: O coeficiente de atrito do cilindro com o chão
: O coeficiente de atrito da prancha com o chão
Utilizando a fórmula que relaciona coeficiente de atrito com força normal e força de atrito, chegamos ao seguinte resultado:
Percebeu que se a gente descobrir o valor dessas forças, a gente descobre os coeficientes de atrito que garantem o equilíbrio?
Passo 3
Vamos aplicar agora as condições de equilíbrio.
Vamos começar pela condição de na prancha.
Para isso, escolheremos o eixo de rotação no ponto em que a prancha encontra o chão. Assim, a força de atrito e a força normal não geram torque. As duas forças que geram torque na prancha são e .
A distância de até o eixo é de .
A distância perpendicular de até o eixo de rotação é de Repare na figura abaixo:
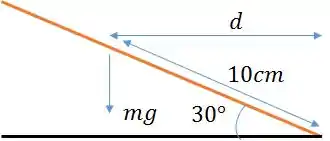
Assim, podemos montar a equação do torque, escolhendo o sentido anti-horário como positivo.
Passo 4
Vamos continuar analisando a prancha.
Podemos aplicar agora as outras condições de equilíbrio:
Antes disso, vamos decompor em e
Dá uma olhada na figura abaixo:
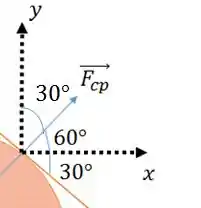
Passo 5
Vamos aplicar para descobrirmos o valor de
Passo 6
Já temos a força normal no ponto em que a prancha encontra o chão. Precisamos da força de atrito no mesmo ponto.
Vamos aplicar para descobrirmos o valor de .
Passo 7
Agora que temos e , podemos calcular o coeficiente de atrito entre a prancha e o chão.
Passo 8
Falta descobrirmos o coeficiente de atrito estático entre o cilindro e o chão.
Então, temos que encontrar e .
Para isso vamos utilizar as equações de equilíbrio para o cilindro.
Já sabemos que por serem forças de ação e reação, as forças e são iguais.
A força tem o mesmo módulo da força e sentido contrário.
A força tem o mesmo módulo da força e sentido contrário.
Passo 9
Vamos aplicar para o cilindro para descobrirmos o valor de .
Passo 10
Já temos a força normal no ponto em que o cilindro encontra o chão. Precisamos da força de atrito no mesmo ponto.
Vamos aplicar para descobrirmos o valor de .
Passo 11
Agora que já temos e podemos achar o coeficiente de atrito entre o cilindro e o chão.
Fim!!! Achamos os valores dos coeficientes de atrito que garantem o equilíbrio estático!
Resposta
Coeficiente de atrito estático entre a prancha e o chão:
Coeficiente de atrito estático entre o cilindro e o chão: